§4-2　电场强度通量　高斯定理

一、电场线

为了形象地描述电场的分布情况，在电场中描绘一系列曲线，使这些曲线上每一点的切线方向都与该点场强E的方向一致。这些曲线称之为电场线（图4-8）。并且，为了表示场强的大小，规定在电场的任一点处，垂直于E的单位面积上，通过电场线的数目等于该点处E的量值，即任一点曲线的密度都等于该点电场强度的大小，则

其中，dS_⊥为过该点并垂直于该点电场强度方向的面积元；dN为通过该面积元的电场线数。显然，这样设置的电场线，不仅能表示电场强度的方向，而且还能表示出电场强度的大小。静电场的电场线具有如下性质：

（1）起始于正电荷（或无限远处），终止于负电荷（或无限远处），不会在无电荷处中断。

（2）任何两条电场线都不会在无电荷处相交，也不会形成闭合回线。

图4-9是几种常见电荷的电场线。

二、电场强度通量

在电场中，通过任一给定面的电场线数，称为通过这个面的电场强度通量，用Φ_e表示。下面分别讨论均匀电场和非均匀电场中的电场强度通量Φ_e。

在均匀电场中，电场强度的大小和方向处处相同，所以电场线为疏密均匀的平行直线簇。这时，通过与电场强度垂直的平面的电场强度通量为电场线密度和面积的乘积[图4-10（a）]，即

Φ_e=ES

若平面与均匀电场强度不垂直，设其法线方向的单位矢量en与电场强度E之间夹角为θ（图4-10（b）]，则它垂直于E的投影面积为S_⊥=Scosθ，故通过该面积的电场强度通量为

Φ_e=EScosθ

对于非均匀电场的情况，在计算通过某一给定曲面的电场强度通量时，可以把曲面划分为无穷多个面积元dS[图4-10（c）]，每个小面积元可视为平面，且在面积元上的电场强度可视为均匀的。设dS法线方向的单位矢量en与面积元上电场强度E的夹角为θ，则通过该面积元的电场强度通量为

dΦ_e=EdScosθ

若定义面积元矢量为dS，其大小为面积元的面积dS，其方向与其法线的方向一致，则上式可以写成标积的形式

dΦ_e=EdScosθ=E·dS

通过曲面S的电场强度通量Φe等于通过曲面上所有面积元的电场强度通量之和，即

Φ_e=∫dΦ_e=∫SEdScosθ=∫SE·dS（4-13）

若曲面S为闭合曲面，则通过闭合曲面的电场强度通量为

Φ_e=∮SEcosθdS=∮SE·dS

式中，积分沿整个闭合曲面进行。

一般规定，闭合曲面上某点的法线方向为垂直该面积元，且由闭合曲面内指向外面的方向（图4-11）。因此，若电场线由闭合曲面内穿出时电场强度通量为正，反之为负。

三、高斯定理

既然电场线可用来描述电荷所激发的电场，那么，电荷与起、止于它的电场线之间应存在一定的关系。德国物理学家高斯（C.F.Gauss，1777—1855）通过缜密研究，得出了反映静电场重要性质的一个基本规律，称为高斯定理。下面来逐步导出这个定理。

首先，我们讨论点电荷处在球面中心的情况。设在以r为半径的球面中心有一点电荷q（设q＞0），则球面上各点的电场强度大小为

其方向沿半径向外[图4-12（a）]。故通过该球面的电场强度通量为

由此表明，通过球面的电场强度通量，只与球面包围的电荷量有关，而与球面半径无关。

显然，当球面中心之点电荷q为负值时，穿过球面的电场强度通量也为负值，故不论点电荷为正值或负值，Φ与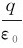的代数值总是相等的。

一般情况下，点电荷q被任意闭合曲面S′包围时，可以点电荷所在处为球心，作球面S包围曲面S′[图4-12（b）]，由于电场线不会在无电荷处中断，故通过闭合面S′的电场强度通量与通过闭合球面S的电场强度通量相同。如果闭合曲面S′内无电荷[图4-12（c）]，由于电场线的连续性，穿入S′的电场线数一定等于穿出S′的电场线数，故通过闭合曲面S′的电场强度通量为零。

根据以上讨论的结果，我们再来论证在闭合曲面内外分布多个点电荷的情况。设共有q₁、q₂、……q_k、q_k+1、……q_n个点电荷，它们单独激发的电场强度分别用E₁、E₂、……E_k、E_k+1、……E_n表示。其中q₁、q₂、……q_k在闭合面S内，q_k+1、q_k+2、……q_n在闭合面S外部[图4-11（d）]。闭合面S上任何一点的电场都是这n个点电荷共同激发的，即E=E₁+E₂+……+E_k+E_k+1+……+E_n，则通过闭合面S的电场强度通量为

由于q_k+1、q_k+2、……q_n在闭合面S之外，则

∮_SE_i·dS=0（i=k+1，k+2，……n）(www.daowen.com)

所以，通过闭合面S的电场强度通量为

所以，在真空中，通过任何一个闭合面的电场强度通量，等于该闭合面内所有电荷的代数和除以ε₀，与闭合面外的电荷无关，此即为真空中静电场的高斯定理。一般表示为

其中，∑q_i为闭合面内电荷的代数和。

对高斯定理的理解，应注意以下两点：

（1）高斯定理表达式中的场强E是曲面上各点的场强，它是由闭合曲面内、外的所有电荷共同产生的合场强，并非只是由闭合曲面内的电荷所产生。

（2）通过闭合曲面的电场强度通量，决定于它所包围的电荷，即只有闭合曲面内的电荷对这一电场强度通量有贡献，而与闭合曲面外的电荷无关。

高斯定理表明静电场是有源场，而且定量的电荷所发出或吸收的电场线数量是一定的。高斯定理表达式（4-15）是电磁场理论的基本方程之一。

虽然高斯定理是在库仑定律的基础上得出的，但高斯定理的应用范围比库仑定律更广泛。库仑定律只适用于静电场，而高斯定理对静电场和变化电场都适用。如果突破历史发展的原因，把高斯定理升格为高斯定律，在静电场中导出库仑定理，在理论上可能更为合理。

四、高斯定理的应用

利用高斯定理，可以对各种情况下的电荷与其电场关系进行分析。此外，它的一个重要应用是计算带电体周围的电场强度。利用高斯定理计算电场强度时，要求所得出的方程中只出现电场强度一个未知量。但是，电场强度一般是随空间位置变化的，要满足上述条件，就必须根据电荷、电场分布的对称性，恰当地选取闭合曲面。下面举例说明这种方法。

例4-6　求均匀带电球面内外的电场强度分布。已知球面半径为R，所带电荷量为+q。

解　由于电荷分布是球对称的，所以电场强度E的分布也是球对称的。因此，在静电场中任意点P的电场强度E的方向都沿半径；而E的大小则仅依赖于从球心到场点P的距离r。在同一球面上各处E的大小相等，且E与球面各处的dS相垂直。取高斯面为过P点的同心的球面，通过它的电场强度通量为

∮_SE·dS=E∮_SdS=E4πr²

当场点P在带电球面外（r＞R）时，此高斯面内包围的电荷量为q。根据高斯定理得

于是点P的电场强度大小为

其矢量表示为

式中，e_r为沿径矢的单位矢量。上式表明，均匀带电球壳在其外部产生的电场强度与等量电荷全部集中在球心时产生的电场强度相同。

若P点在带电球面内（r＜R），则高斯面内没有电荷，即

∑q=0

由高斯定理可得

∮_SE·dS=E4πr²=0

即均匀带电球壳内部的电场强度为零。

E=0

以上结果说明，在均匀带电球面内部，电场强度处处为零，在球面外部，电场强度E与r的平方成反比。E和r的函数关系如图4-13所示。

例4-7　求无限大均匀带电平面周围的电场强度。已知其面电荷密度为σ。

解　由于均匀带电平面是无限大的，所以带电平面两侧的电场具有对称性。由对称性分析可知，在带电平面两侧与平面等距离处各点的电场强度E的大小相等，方向与带电平面垂直，如图4-14所示。取垂直通过带电平面，且相对带电平面对称的闭合圆柱面为高斯面。其侧面的法线与电场强度垂直，故通过其侧面的电场强度通量为零。而在两底面上各点的电场强度大小相等，方向与底面垂直。所以，通过该高斯面的电场强度通量为

Φ_e=∮_SE·dS=∫_底E·dS+∫侧E·dS=2ES

此高斯面所包围的电荷量总和为σS，根据高斯定理有

所以，底面处电场强度大小为

无限大均匀带电平面两侧的电场是均匀电场，其方向与带电平面垂直。

利用电场强度的叠加原理不难证明，两个面电荷密度为等量异号的无限大均匀带电平行平面之间的电场强度的大小为

两带电平面外侧的电场强度为零，如图4-15所示。