一、电荷

两种不同材料的物体，如丝绸和玻璃棒相互摩擦后，它们都能吸引羽毛、小纸片等轻小物体。这时，我们说丝绸和玻璃棒处于带电状态，此时它们分别带有电荷。可见，电荷是物体的一种属性。宏观物体或微观粒子处于带电状态，就说它们带有电荷。

实验证明，物体或微观粒子所带的电荷只有两种，称为正电荷和负电荷。同号电荷相互排斥，异号电荷相互吸引，这种相互作用力称为电力。根据带电体之间相互作用力的大小，可以确定物体所带电荷的多少。表示电荷多少的物理量称为电荷量，简称电荷。电荷量的单位为库仑，用C表示。

在一个孤立系统中，无论发生怎样的物理过程，该系统电荷量的代数和均保持不变，这就是电荷守恒定律。实验表明，无论在宏观领域还是在微观过程中，这一定律都是成立的。

实验表明，任何带电体所带的电荷量都是基本电荷量e=1.602×10^-19C的整数倍，这种电荷量只能取分立的、不连续的量值的性质称为电荷的量子化。1897年，汤姆孙（J.J.Thomson，1856—1940）发现了电子。1919年，人们又发现了质子。由检测得知，电子和质子所带电荷量的绝对值都等于基本电荷量。

由于电荷的基本单元很小，因而，一般的宏观过程中涉及的电荷量总是包含着大量的基本单元。致使在研究宏观现象时，可以不考虑电荷量的量子化，仍可认为宏观物体上的电荷是连续分布的，它所带的电荷量是可以连续变化的。

二、库仑定律

两个静止带电体之间的作用力，不仅与它们所带的电荷量及它们之间的距离有关，而且与它们的大小、形状及电荷分布情况有关。当带电体本身的线度与它们之间的距离相比足够小时，其形状、大小可以忽略，可视为点电荷。

1785年，库仑（Coulomb，1736—1806）通过扭秤实验，总结出两个静止点电荷之间相互作用的规律，称为库仑定律：在真空中，两个静止点电荷之间相互作用力的大小与它们电荷量的乘积成正比，与它们之间距离的平方成反比；作用力的方向沿着两点电荷的连线，同号电荷相斥，异号电荷相吸。如图4-1所示，由点电荷q₁至点电荷q₂的矢量用r₁₂=r₁₂e₁₂表示，e₁₂为r₁₂的单位矢量，那么q₁对q₂的作用力F₁₂为

式中，k为比例系数，其数值和单位取决于式中各量所采用的单位，在国际单位制中，k=8.98755×10⁹N·m²/C²≈9.0×10⁹N·m²/C²。

为了方便，又引入另一个常量ε₀=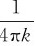，即k=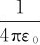，这样代入式（4-1）后就得到了库仑定律的常用表达式：

常量ε₀称为真空介电常数，又称真空电容率，在SI单位制中，它的数值和单位是

ε₀=8.854×10^-12C²/（m²·N）=8.854×10^-12F/M

在空气中两个点电荷的作用力和在真空中的结果十分相似，所以式（4-1）和式（4-2）也适用空气中的情况。

实验表明，任何两个点电荷之间的静电力都遵守库仑定律，并不因附近存在其他电荷而改变。当空间同时存在两个以上的点电荷时，作用于某一点电荷上的总静电力等于其他各点电荷单独存在时，对该点电荷所施静电力的矢量和，这就是静电力的叠加原理。

三、电场

我们知道，两个彼此不相互接触的物体之间的相互作用，是依赖其周围空间的物质作为介质来传递的。近代物理学的观点认为，电荷在周围空间激发电场，电场的基本特性是对处于其中的电荷施以作用力。因此，电荷之间的相互作用是通过它们所激发的电场来传递的。这种相互作用可由如下示意图表示：

相对于观察者静止的电荷所激发的电场，称为静电场。由于静电场对处于其中的电荷具有作用力，所以当电荷在静电场中移动时，电场力就要对电荷做功，表明电场具有能量。近代物理学已证实，电场和一切实物一样，不仅具有能量，而且还有动量和质量等重要性质。由此表明，电场也是一种物质形态，但场与其他物质不同，几个电场可以同时占有同一空间。所以，电场是一种特殊的物质。

四、电场强度

处于电场中的任何带电体都受到电场所施的作用力，这是电场的基本性质。根据这一性质，可从电荷在电场中受力的特点来定量描述电场中任一点的性质。利用电荷量很小的点电荷q0作为试验电荷，不仅可以检验电场是否存在，而且也可以定量地研究空间各点电场的差异。

当在电场中某给定点放置不同的试验电荷时，它所受的电场力F的大小与试验电荷的电荷量q0成正比，F的方向随q₀的符号变化，而比值F/q₀为恒量。若把同一试验电荷q₀分别放在电场中的不同位置，一般来说，比值F/q₀也将随之改变。由此表明：比值F/q₀与试验电荷无关，而只与试验电荷所在处的电场状况有关。因此，我们可以把比值F/q₀作为描述电场性质的物理量，称之为电场强度，用E表示，定义

电场中某点的电场强度在数值上等于单位试验电荷在该点所受的作用力的大小，其方向与正电荷在该点所受电场力的方向一致。

在国际单位制中，电场强度的单位为牛顿/库仑（N/C）或伏特/米（V/m）。

一般情况下，电场中的不同位置，其场强的大小和方向各不相同，要完整地描述整个电场，必须知道各点的强度分布，即求出矢量场函数E=E（r）。

五、电场强度的计算

应当指出，计算电场强度可以通过不同的方法，下面阐述如何通过场源电荷计算它所激发电场的电场强度。

1.点电荷的电场

如图4-2所示，q为真空中静止的点电荷，P为其电场中的一点，由q至P点的矢量r=re_r，e_r是沿r方向的单位矢量。若将试验电荷q₀置于P点，根据库仑定律，q0所受的电场力为

由电场强度定义式（4-3）可得P点的电场强度为

上式表明，场源点电荷q在P点激发的电场强度，大小与点电荷的电荷量成正比，且与P点到点电荷的距离的平方成反比。电场强度E的方向与场源电荷q的正负相关。q＞0时，E与e_r同向；q＜0时，E与e_r反向，即指向场源电荷q。

2.场强叠加原理与点电荷系的场强

若电场是由多个点电荷q₁、q₂、……q_n共同激发的，根据力的叠加原理，试验电荷q₀在P点所受到的电场力为F=F₁+F₂+……+F_n，式中，F₁、F₂……F_n分别为q₁、q₂、……q_n单独存在时，q₀在P点所受的电场力，根据电场强度的定义，P点的电场强度为

即

上式表明，在点电荷系所激发的电场中，任一点的电场强度等于各个点电荷单独存在时在该点所产生的电场强度的矢量和，这就是电场强度的叠加原理。

若用e_i表示由第i个点电荷q_i到P点的矢径r_i方向的单位矢量，根据式（4-4）则有

根据场强叠加原理，可得点电荷在P点的总场强为

例4-1　如图4-3所示，在直角坐标系的原点（0，0）及离原点1.0m的y轴上（0，1）处分别放置电荷量为q₁=1.0×10^-9C和q₂=-2.0×10^-9C的点电荷。求x轴上离原点为2.0m处P点的场强。

解　q₁在P点激发的场强为

q₂在P点激发的场强大小为

E_2x=-3.6cosα=-3.2N/C

E_2y=3.6sinα=1.6N/C

E₂=（-3.2i+1.6j）N/C

则

E=E₁+E₂=[（2.3-3.2）i+1.6j]=（-0.9i+1.6j）N/C

例4-2　如图4-4所示，两个等量异号点电荷+q和-q相距l。求这两个点电荷连线的中垂线上，距垂足为r的P点处的电场强度。(www.daowen.com)

解　设+q和-q分别在P点产生的电场强度为E+和E-，则P点的电场强度E=E++E-。因为+q和-q到P点的距离都是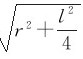，所以E+和E-的大小相等，其值为

由对称性知

E_-y=-E_+y，E_y=E_-y+E_+y=0

E_+x=E_-x=-E+cosα

E_x=E_+x+E_-x=-2E+cosα

其中

所以，P点的场强大小为

方向沿x轴的负方向。

当场点P到两点电荷的距离r＞＞l时，则称这两个点电荷构成的电荷系为电偶极子，从-q到+q的矢径l称为电偶极子的极轴，p=ql称为电偶极子的电偶极矩。由于r＞＞l，则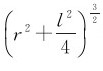，≈r³，因而，电偶极子中垂线上P点的电场强度可表示为

3.连续分布电荷的电场

通常，由仪器能观测到的最小电荷量中都包含着大量的基本电荷。从宏观角度看，任何带电体上的电荷都是连续分布的。在带电体上的极小区域内的电荷元可视为点电荷，整个带电体则可看成是由许多点电荷组成的。

设由电荷元dq到P点的矢径为r, r方向的单位矢量为e_r，则电荷元dq在P点所激发的场强为

根据场强叠加原理，整个带电体在P点激发的场强是所有电荷元在P点激发的场强dE的矢量和，即

在带电体上电荷的分布，又可分为体分布、面分布和线分布三种情况，其相应的场强计算式又可分别写成

式中，ρ为电荷体密度；σ为电荷面密度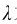；为电荷线密度。上式为矢量积分式，在具体运算时，往往须先把它们在三个坐标轴方向上的分量写出，而作分量积分。

例4-3　如图4-5所示，一均匀带电有限长直线，其线电荷密度为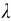，线外P点到直线的垂直距离为a, P点和直线两端的连线与直线之间的夹角分别为θ₁和θ₂。求P点的电场强度。

解　建立如图4-5所示坐标系，P到直线的垂足O为坐标原点。在坐标为x处，取长为dx的直线段为电荷元，其电荷量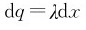，该电荷元在P点产生的场强dE的大小为

dE的方向与x轴的夹角为θ，它沿x、y轴的分量分别为

dE_x=dEcosθ，dE_y=dEsinθ

所以

由图中几何关系知

x=acot（π-θ）=-acotθ

dx=acsc²θdθ

将此结果代入上式可得

则P点的电场强度为

如果这一均匀带电直线为无限长，即θ₁=0，θ₂=π，则有

例4-4　如图4-6所示，电荷量q均匀分布在半径为R的细圆环上（设q＞0）。求圆环轴线上任一点P的电场强度。

解　沿轴线建立如图4-6所示的坐标系，原点在圆环中心，设P点坐标为x。在圆环上取长为dl的线元作为电荷元，其电荷量dq=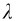dl，其中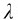=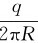为线电荷密度。电荷元在P点产生的电场强度为dE，它在平行和垂直x轴方向的分量分别为dE_//和E，则P点的电场强度

E=∫dE=∫dE_//+∫dE_⊥

由于电荷分布的对称性，显然

∫dE_⊥=0

则P点的电场强度为

显然，q＞0时，E沿x轴正方向；q＜0时，E的方向沿轴线指向环中心O点。

当x＞＞R时，E≈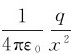，即整个带电圆环可近似视为点电荷。

例4-5　半径为R的圆盘均匀带电，面电荷密度为σ。求圆盘轴线上任一点的电场强度。

解　如图4-7所示，在圆盘上取半径为r，宽度为dr的同心圆环带，可视为均匀带电细圆环。其带电荷量为dq=σ2πrdr，它在轴线上P点产生的电场强度大小为

均匀带电圆盘可看成由许多同心均匀带电圆环组成，它们在P点产生的电场强度方向相同，故P点的电场强度大小为

如果我们计算的场点P靠近圆盘面，即x＜＜R，则

此时，可将带电圆盘看做无限大的带电平面，可见无限大均匀带电平面产生的电场为均匀电场。

六、电场力

已知电场，我们则可以计算处于电场中的电荷所受的电场力。

由式（4-3）可知，点电荷q在电场强度为E处所受的电场力为

F=qE

对于处于外电场中的点电荷系所受的电场力，则可根据电场力的叠加原理来计算。对于带电体的情况，可把带电体划分为许多可视为点电荷的电荷元，先计算每个电荷元所受的电场力，然后再通过积分求其所受的合力。