§3-4　角动量　角动量守恒定律

在上一章中，我们研究了力对改变质点运动状态所起的作用。我们曾从力对空间的积累作用出发引出动能定理，从而得出机械能守恒定律；从力对时间的累积作用出发，引出动量定理，从而得到动量守恒定律。对刚体的定轴转动，我们采用了同样的研究方法讨论了力矩对空间的累积作用，得出刚体转动的动能定理；本节我们将讨论力矩对时间的积累作用，得出角动量和角动量守恒定律。

在研究质点的平动时，我们用质点的动量来描述质点的运动状态。当研究刚体的转动问题时，例如，研究圆盘型匀质飞轮绕通过其中心且垂直于飞轮平面的定轴转动，虽然飞轮在转动，但按质点系动量的定义，其总动量为零。这说明仅用动量来描述物体的机械运动是不够的，为此我们需要引进另一物理量——角动量。本章我们来讨论角动量所遵从的规律。

一、质点的角动量和角动量守恒定律

1.质点的角动量

设质量为m的质点某一时刻的运动速度为υ，该时刻质点相对于原点O的位矢为r，如图3-16（a）所示，则质点的动量为p=mυ。我们定义质点m相对原点O的角动量为

L=r×p=r×mυ

质点的角动量L是一个矢量，其大小为

L=rmvsinθ

式中，θ为r和mυ间的夹角，L的方向由右手螺旋法则确定，把右手拇指伸直，其余四指由矢径r通过小于180°的角弯向υ，拇指所指的方向就是L的方向，如图3-16（b）所示。

若质点做半径为r的圆周运动，如图3-17所示，某一时刻质点位于A点，速度为v，如以圆心O为参考点，那么r与υ总是相垂直的。质点对圆心O的角动量L的大小为

L=rmv=mr²ω

L的方向应平行于Oz轴，且与ω的方向相同。

应当指出，质点的角动量L与矢径r和动量p有关，也就是与参考点O的选择有关。因此在表述质点的角动量时，必须指明是对哪一点的角动量。在涉及质点的圆周运动问题中，多以圆心为参考点来表述角动量，所以角动量是描述转动状态的物理量。例如，在微观粒子的运动中，不仅有电子绕原子核运动的轨道角动量，还有粒子本身自旋的角动量等。

在国际单位制中，角动量的单位是kg·m²/s

2.质点的角动量守恒定律

根据质点的角动量L=r×mυ，两边对时间t求导得

由于

故上式可写成为

由矢积性质知道，υ×mυ=0，而r×F=M，因此有

上式表明：质点所受的合外力矩等于质点的角动量对时间的变化率。这是质点角动量定理的一种表示形式，其中合外力矩和角动量都是相对同一参考点而言的。

式（3-22）与牛顿第二定律F=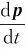在形式上是相似的，只是用M代替了F，用L代替了p。如果质点所受的合外力矩为零，即M=0，则有

L=r×mυ=恒矢量

这就是说，相对于某一参考点，如果质点所受的合外力矩为零，则质点的角动量保持不变，这就是质点的角动量守恒定律。

应当注意，质点角动量守恒的条件是合外力矩M=0。这可能有两种情况：一是合力F=0；另一种是合力F虽不为零，但力的作用线通过参考点（这样的力称为有心力，参考点为力心）致使合外力矩为零，质点做匀速圆周运动就是这样的例子，作用于质点的合力是指向圆心的向心力，故其力矩为零，此时，质点对圆心的角动量是守恒的。另外，只要作用于质点的力是有心力，其对力心的力矩总为零，所以在有心力作用下质点对力心的角动量都是守恒的。行星绕太阳的运动、卫星绕地球的运动、电子绕原子核的运动等都是在有心力作用下的运动，故它们的角动量都是守恒的。

例3-9　我国第一颗人造地球卫星绕地球沿椭圆轨道运动，地球的中心为椭圆的一个焦点。已知人造地球卫星近地点的高度l₁=439km，远地点高度l₂=2384km，如图3-18所示，卫星经过近地点时的速率v₁=8.10km/s，求卫星在远地点的速率。取地球半径R=6378km，空气阻力不计。

解　由于卫星在运行中只受到地球引力的作用，而引力始终指向地心，即卫星受到有心力的作用，所以卫星对地心的角动量守恒，即

L=rmvsinθ=常量

在近地点和远地点，θ=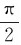，所以

mv₁（R+l₁）=mv₂（R+l₂）

由此得

二、刚体的角动量和角动量守恒定律

前面我们介绍了质点的角动量概念，下面把这一概念扩展到刚体定轴转动的情形。

1.刚体的角动量

如图3-19所示，刚体绕Oz轴以角速度ω转动，刚体上每一质点都以相同的角速度ω绕Oz轴做圆周运动。设刚体中第i个质点的质量为Δm_i，到转轴的距离为ri，根据式（3-21），该质点的角动量为Δm_ir²_iω，则刚体对Oz轴的角动量为

L=∑Δm_ir²_iω=（∑Δm_ir²_i）ω(www.daowen.com)

式中，∑Δm_ir²_i为刚体绕Oz轴的转动惯量J。于是刚体绕定轴Oz的角动量为

L=Jω

其矢量式为

L=Jω

即刚体对转轴的角动量等于其转动惯量与角速度的乘积。

2.刚体的角动量守恒定律

根据转动定理，刚体所受的合外力矩与角加速度的关系为

利用角动量表示式，转动定理可重新表示为

上式表明，刚体绕定轴转动时，作用于刚体的合外力矩等于刚体绕此定轴的角动量对时间的变化率。这是刚体角动量定理的一种表示形式。

与转动定理式（3-11）相比，式（3-25）是转动定理的另一种表达方式，其适用范围更加广泛。当定轴转动物体的转动惯量发生变化时，式（3-11）已不适用，但式（3-25）仍然成立。这与质点动力学中牛顿第二定律的表达式F=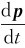较之F=ma更普遍是一样的。

由式（3-25）可知，当合外力矩M为零时，可得

L=Jω=恒量

这就是说，如果物体所受的合外力矩为零，或不受外力矩的作用，物体的角动量保持不变，这一结论就是角动量守恒定律。

必须指出，上面在导出角动量守恒定律的过程中虽然受到刚体、定轴等条件的限制，但它的适用范围非常广泛。

（1）角动量守恒定律不仅适用于刚体。可以证明，该定律对非刚体同样适用。对于转动惯量可以变化的非刚体，当合外力矩M=0时，可得

Jω₁=Jω₂

即当转动惯量变化时，其旋转角速度也随之变化，以使二者的乘积Jω保持不变。当J减小时，ω增大；当J增大时，ω减小。利用改变转动惯量来达到改变旋转角速度的例子很多，如花样滑冰运动员做旋转动作时，往往先把两臂张开旋转，然后迅速收拢两臂靠近身体，使相对身体中心轴的转动惯量迅速减小，从而使旋转速度增大。

（2）角动量守恒定律对天体运动以及微观粒子的运动同样适用。角动量守恒定律与动量守恒定律、能量守恒定律都是自然界的普遍规律，虽然它们都是在不同理想化条件下，在经典的牛顿运动定律的基础上导出的，但适用范围远远超出了原有条件的限制。它们不仅适用于牛顿力学所研究的宏观、低速（远小于光速）领域，而且适用于微观、高速（接近光速）领域。这三条守恒定律是比牛顿运动定律更基本、更普遍的物理规律。

例3-10　工程上，两飞轮常用摩擦离合器使他们以相同的转速一起转动。如图3-20所示，A和B两飞轮的轴杆在同一中心线上，A飞轮的转动惯量为JA=10kg·m²，B飞轮的转动惯量为JB=20kg·m²。开始时，A轮的转速为600r/min, B轮静止。C为摩擦离合器。求两飞轮离合后的转速；在离合过程中，两飞轮的机械能有何变化?

解　把飞轮A、B和离合器C作为一系统来考虑，在离合过程中，系统受到轴的正压力和离合器间的切向摩擦力，前者对转轴的力矩为零，后者为系统的内力矩。故系统受到的合外力矩为零，系统的角动量守恒。所以有

J_Aω_A+J_Bω_B=（J_A+J_B）ω

ω为两轮离合后共同转动的角速度，于是

把各量的数据代入，得

ω=20.9rad/s

或共同转速为

n=200rad/min

在离合过程中，摩擦力矩做功，所以机械能不守恒，部分机械能转化为热能，损失的机械能为

例3-11　长为l、质量为M的匀质细杆，一端悬挂，可绕通过O点垂直于纸面的轴转动。令杆从水平位置由静止开始下落，在铅直位置处与质量为m的物体A做完全弹性碰撞，如图3-21所示。若碰撞后物体沿动摩擦因数为μ的水平面滑动，则物体能滑出多远的距离?

解　该问题可分为三个阶段分析求解。杆自水平位置落到铅直位置，与A碰撞前为第一阶段；杆与物体A的碰撞过程为第二阶段；第三阶段为物体A沿水平面滑动的过程。

第一阶段取杆为研究对象。杆受重力及悬挂轴的作用力。设杆与A碰撞前的角速度为ω，由动能定理

杆对转轴O的转动惯量为J=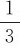Ml²，所以有

第二阶段取杆和物体组成的系统为研究对象。碰撞过程中，系统相对于轴O受到的外力矩为零，故系统的角动量守恒。设碰撞后杆的角速度为ω′，则

Jω=Jω′+ml²ω′

代入J，可解得

第三阶段取物体A为研究对象。设物体在摩擦力作用下可滑过距离s，由质点的动能定理