§3-3　转动中的功和能

刚体受到力矩的作用并绕轴转动时，力矩对刚体做功，做功的结果是使刚体的角速度发生变化，因而其动能也发生相应的变化。本节讨论转动中的功能关系。

一、力矩做功

刚体做定轴转动时，外力对刚体所做的功可用力矩来表示。如图3-14所示，用F表示作用在刚体上P点的外力，当刚体绕Oz轴发生dθ的角位移时，P点的位移为dr，力F所做的元功为

由于Fcosβ是力F沿dr方向的分量，所以Fcosβr就是力对转轴的力矩，因此有

dA=Mdθ

即外力对转动刚体所做的元功等于相应的力矩和角位移的乘积。

对于有限的角位移，外力做的功用积分表示

以上两式中的功常称为力矩的功，显然力矩的功就是把外力的功用描述转动的相关物理量表示出来。如果刚体受到几个力的作用，则上两式中的外力矩应为合外力矩。

二、刚体的转动动能和重力势能

刚体绕定轴转动时，其上每个质点都绕轴做圆周运动，都具有一定的动能，所有质点动能之和就是刚体的转动动能。设刚体中第i个质点的质量为Δm_i，到转轴的距离为r_i，速度为v_i，则该质点的动能为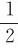Δm_iv²_i，又v_i=ωr_i，因此，整个刚体的动能为

式中，Δm_ir²_i正是刚体对转轴的转动惯量J，所以定轴转动刚体的动能可写为

式（3-16）的动能叫做刚体的转动动能，可以看出，转动动能与质点的动能在形式上相互对应，转动惯量与质量对应，角速度与速度对应。

如果刚体受到保守力的作用，也可引入势能的概念。例如，在重力场中的刚体就具有一定的重力势能，对于一个不太大的质量为m的刚体，它的重力势能应是组成刚体的各个质点的重力势能之和，即

E_p=∑Δm_igh_i=g∑Δm_ih_i

根据质心的定义，此刚体质心的高度为

所以上式可写为

E_p=mgh_C

该结果表明，一个不太大的刚体的重力势能与它的质量集中在质心时所具有的势能一样。

三、定轴转动的动能定理(www.daowen.com)

设在合外力矩M的作用下，刚体绕定轴转过角位移dθ，合外力矩对刚体所做的元功为

dA=Mdθ

由转动定律M=Jα=J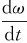，上式可写为

如刚体的角速度由t₁时刻的ω₁变为t₂时刻ω₂，则此过程中的外力矩对刚体做的总功为

即

上式表明，合外力矩对刚体所做的功等于刚体转动动能的增量，这就是刚体定轴转动的动能定理。

对于包含刚体的系统，如果在运动过程中，只有保守内力做功，则该系统的机械能也应守恒。从形式上看，刚体能量守恒定律和质点系的机械能守恒定律完全相同；但对包含刚体的系统来说，既要考虑质点的动能、重力势能、弹性势能，还要考虑刚体的平动动能、重力势能和转动动能。

例3-7　某一冲床利用飞轮的转动动能，通过曲柄连杆机构的传动带动冲头在铁板上钻孔。已知飞轮为均匀圆盘，其半径为r=0.4m，质量为m=600kg，飞轮的正常转速是n₁=240r/min，冲一次孔转速降低20%。求冲一次孔冲头做的功。

解　以ω₁和ω₂分别表示冲孔前后飞轮的角速度，则

ω₂=（1-0.2）ω₁=0.8ω₁

由转动动能定理式（3-18）可得冲一次孔铁板阻力对冲头做的功为

因J=mr²，代入数据得

A=-5.45×10³J

这是冲一次孔铁板阻力对冲头做的功，它的大小也就是冲一次孔冲头克服此阻力做的功。

例3-8　如图3-15所示，一半径为R、质量为M的圆盘滑轮可绕通过盘心的水平轴转动。滑轮上绕有轻绳，绳的一端悬挂质量为m的物体。当物体从静止下降距离h时，物体的速度是多少?

解　以滑轮、物体和地球组成的系统为研究对象。由于只有保守内力做功，系统机械能守恒。

设物体开始下降时为初态，下降高度h后为终态，并设终态时重力势能为零。初态时：动能为零，重力势能为mgh；终态时：动能包括滑轮的转动动能和物体的平动动能，由机械能守恒定律

滑轮的转动惯量J=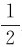MR²，物体下落速度与滑轮的角速度之间的关系为v=Rω，由此可解得