§3-2　转动定理

上一节我们讨论了刚体的运动学问题，从本节开始，将讨论刚体定轴转动动力学问题，即研究刚体获得角加速度的原因。研究定量描述刚体做定轴转动时遵从的动力学规律——转动定理。

一、力矩

为了改变刚体原来的运动状态，必须对刚体施力的作用，经验告诉我们，外力对刚体转动的影响，不仅与作用力的大小有关，而且还与作用力的方向和力的作用点的位置有关。例如，开关门窗时（图3-4），当力F的作用线通过转轴或平行于转轴，就无法使门窗转动。

力的大小、力的方向和作用点相对于转轴的位置，是决定转动效果的几个重要因素。将这几个因素一并考虑，引入力矩这一概念。

如图3-5（a）所示，若作用于物体的力F在转动平面内，力的作用点相对于转轴的位矢为r，力臂为d，我们定义：力的大小与力臂的乘积为力对转轴的力矩，用M表示，即

M=F·d=Frsinθ

若作用于物体的力F不在转动平面内，如图3-5（b）所示，可将力分解为垂直于转轴z的分量F⊥和平行于转轴的分量F//，平行于转轴的分力F//不能改变刚体的转动状态，对转轴不产生力矩，垂直于转轴的分力F⊥位于转动平面内，它产生的力矩与式（3-6）相同，因此，我们只需考虑垂直于转轴的作用力。

应当指出，力矩不仅有大小，而且有方向。力矩是矢量。由矢量的矢积定义，力矩矢量M可用矢径r和力F的矢积表示，即

M=r×F

M的方向垂直于r和F所构成的平面，也可由图3-6所示的右手法则所确定：把右手拇指伸直，其余四指由矢径r通过小于180°的角弯向F，拇指所指的方向就是力矩的方向。

二、转动定理

在研究质点的运动时，我们知道，在外力作用下，质点会获得加速度。做定轴转动的刚体，在外力矩作用下，角速度会发生变化，即获得了角加速度。下面我们从牛顿第二定律出发推导出刚体角加速度和外力矩之间的关系。

如图3-7所示的刚体，其转轴Oz固定于惯性系中，刚体可看做由许多质点组成，在刚体中任取一质点i，其质量为Δm_i，旋转半径为r_i，所受到的合外力为F_i，刚体内其他质点作用的合内力为f_i，并设外力F_i与内力f_i均在与Oz轴垂直的同一平面内。质点i的加速度为a_i，由于法向力通过转轴，不产生力矩，法向加速度与角加速度无关。我们只考虑切向方向，由牛顿第二定律得

F_it+f_it=Δm_ia_it

又a_it=r_iα，所以有

F_it+f_it=Δm_ir_iα

两边同乘以ri，得

F_itr_i+f_itr_i=Δm_ir²_iα

式（3-8）左边两项分别为外力F_i和内力f_i对转轴的力矩。若遍及刚体内的所有质点，由式（3-8）可得

可以证明，所有内力矩的总和为零。先考虑一对内力矩，如图3-8所示，任意两质点i和j之间的相互作用力分别为f_ij和f_ji，f_ij和f_ji大小相等，方向相反，处于同一条直线上，对Oz轴的力臂同为d，所以两者力矩之和为零。由于内力总是成对出现的，故刚体内所有内力矩的总和为零。即

∑f_itr_i=0

这样，可得到

∑F_itr_i=∑（Δm_ir²_i）α

∑F_itr_i为刚体内所有质点所受到的外力对转轴的力矩之和，即为合外力力矩。用M表示，这样上式为

M=∑（Δm_ir²_i）α

式中，∑（Δm_ir²_i）由刚体内各质点相对于转轴的分布所决定，它只与绕定轴转动的刚体本身的性质和转轴的位置有关，叫做转动惯量。对于绕定轴转动的刚体，它为一恒量，用J表示，即

J=∑（Δm_ir²_i）

这样，有

M=Jα

上式表明，绕定轴转动的刚体，其角加速度与它受到的合外力矩成正比，与刚体的转动惯量成反比，这一结论就是刚体定轴转动定理。如同牛顿第二定律是解决质点运动问题的基本定律一样，转动定理是解决刚体定轴转动问题的基本方程。

三、转动惯量

把转动定理与牛顿第二定律相比较，二者的表达式很相似，M=Jα与F=ma比较，合外力矩M与合外力F相对应，角加速度α与加速度a相对应，转动惯量J与质量m相相应。由此可见，转动惯量是刚体转动时转动惯性大小的量度，即以相同的力矩作用于两个绕定轴转动的不同的刚体上，转动惯量大的刚体获得的角加速度小，其角速度改变得慢，也就是保持原有转动状态的惯性大；反之，转动惯量小的刚体获得的角加速度大，其角速度改变得快，保持原有转动状态的惯性就小。转动惯量的定义式为

J=∑（Δm_ir²_i）

即刚体的转动惯量等于刚体内各质点的质量与其到转轴距离平方的乘积之和。对于质量离散分布的转动系统，可直接用定义式来计算转动惯量。对于质量连续分布的刚体，转动惯量式中的求和应以积分来代替，即

J=∫r²dm

积分式中的dm为质元的质量，r为质元到转轴的距离。

在国际单位制中，转动惯量的单位是kg·m²。

计算转动惯量时，可根据刚体质量分布的不同，引入相应的质量密度，建立质元质量dm的具体表达式，然后进行积分运算。下面通过具体的例子来说明。

1.刚体质量为线分布（细杆状刚体）

例3-3　求质量为m、长为L的均匀细杆的转动惯量。

（1）转轴通过杆的中心并与杆垂直；

（2）转轴通过杆的一端并与杆垂直。(www.daowen.com)

解　引入质量线密度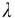，即单位长度的质量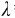=m/L。

（1）如图3-9（a）所示，取杆中心为坐标原点O, x轴方向如图所示。在细杆上任意位置x处，取一长度为dx的线元，其质量dm=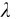dx，该质量元绕转轴的转动惯量为

由于转轴通过杆中心，所以转动惯量为

（2）对于通过杆端点的轴，如图3-9（b）所示建立坐标。

结果表明，同一刚体对于不同转轴的转动惯量不同，可以证明，通过质心的转动惯量最小。我们可以导出一个相对于不同转轴的转动惯量之间的一般关系。用m表示刚体的质量，用JC表示通过其质心C的轴zC的转动惯量，如果另一个轴z′相对质心轴zC平行且相距为d，如图3-10所示。可以证明，刚体对通过z′轴的转动惯量为

J=JC+md²

上述关系叫做转动惯量的平行轴定理，平行轴定理不仅有助于计算转动惯量，而且对研究刚体的滚动也很有帮助。

2.刚体质量为面分布（薄板状刚体）

例3-4　一均匀圆盘质量为m，半径为R。求通过盘中心并与盘面垂直的轴的转动惯量。

解　引入质量面密度σ，即单位面积的质量σ=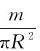

薄圆盘可以看做是许多同心圆环的集合，如图3-11所示，在圆盘上任取一半径为r，宽度为dr的窄圆环，圆环的面积为2πrdr，圆环的质量dm=σ·2πrdr。此窄圆环上各点到转轴的距离都为r，该圆环对通过盘心垂直于盘面的轴的转动惯量为

dJ=r²dm=2πσr³dr

整个圆盘对该轴的转动惯量为

在实际应用中，经常会遇到由几部分不同形状和大小的物体构成的一个整体，根据转动惯量的定义，其转动惯量应等于各部分物体对同一转轴转动惯量之和。

由转动惯量的定义以及上述有关转动惯量的计算结果可以看出，刚体的转动惯量与下列三个因素有关：

（1）与刚体的总质量有关。总质量越大，刚体的转动惯量越大。

（2）与质量分布有关。刚体上质量分布离轴越远，转动惯量越大。

（3）与转轴的位置有关。

综上所述，对于几何形状对称、质量分布连续且均匀分布的刚体，可以用积分的方法算出转动惯量。对于任意刚体的转动惯量，通常是用实验的方法测定出来的。表3-1列出了一些常见刚体的转动惯量。

表3-1　几种几何物体的转动惯量

四、转动定理应用举例

刚体定轴转动定理定量地反映了物体所受到的合外力矩、转动惯量和转动角加速度之间的关系，它在转动中的地位与牛顿第二定律相当，应用转动定理解决的定轴转动问题一般也可分为两类：一类是已知力矩求转动；另一类是已知转动求力矩。在实际问题中常常两者兼有。

应用转动定理求解问题的方法和步骤也与牛顿第二定律的应用相类似，下面我们举例来说明转动定理的应用。

例3-5　如图3-12所示，轻绳跨过一定滑轮，滑轮视为圆盘，绳的两端分别悬有m₁和m₂的物体，且m₁＜m₂，设滑轮的质量为M，半径为R。绳与滑轮间无相对滑动，求物体的加速度和绳中的张力。

解　质点动力学中，涉及有关滑轮的问题时，为简单起见，都假设滑轮的质量忽略不计。但在计及滑轮质量时，就必须考虑滑轮的转动。本例中，m₁和m₂做平动，它们的加速度a取决于每个物体所受的合力。而滑轮做转动，其角加速度取决于作用于其上的合外力矩。

首先将三个物体隔离出来，进行图3-12所示的受力分析，其中张力T₁和T₂的大小不能假定相等，但T₁=T′₁，T₂=T′₂，应用牛顿定律，对物体m₁和m₂有

T₁-m₁g=m₁a

m₂g-T₂=m₂a

而对滑轮，由于转轴通过轮的中心，在T′₁和T′₂的力矩作用下，由转动定理

T′₂R-T′₁R=Jα

其中，J=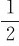MR²为滑轮的转动惯量。由于绳相对滑轮无滑动，在滑轮边缘上一点的切向

加速度和绳与物体的加速度大小相等，与滑轮角加速度的关系为a=Rα。由以上各式解得

例3-6　一长为l、质量为m的均匀细直杆，可绕通过其一端且与杆垂直的光滑水平轴转动，如图3-13所示。将杆由水平位置静止释放，求它下摆角为θ时的角加速度和角速度。

解　杆的向下摆动可视为刚体的定轴转动，重力矩是杆产生转动的唯一原因。而重力矩可等价于杆的质量全部集中在杆的中点时重力产生的力矩，为

由转动定理M=Jα，得角加速度为

因为

故有

分离变量有

两边积分

得到

角速度为