刚体的运动分为平动和转动两种。而转动又可分为定轴转动和非定轴转动。如果刚体内任意两点间的连线在运动过程中始终保持平行，则刚体的这种运动称为平动，如图3-1所示。刚体的平动可看做是质点的运动，描述质点运动的各个物理量和质点力学的规律都适用于刚体的平动。

当刚体中所有点都绕同一直线做圆周运动，这种运动称为转动，这条直线叫做转轴。如果转轴的方位在刚体运动过程中随时间变化，这是非定轴转动；如果转轴在运动过程中，既不改变方向也不平移，则这个转轴称为固定转轴，此时刚体的转动为定轴转动。本章我们主要研究刚体的定轴转动。

一般的刚体运动可看做是平动和转动的合成运动，所以刚体平动和转动的规律是研究刚体复杂运动的基础。

同质点力学一样，刚体的定轴转动同样可分为运动学和动力学，本节我们首先学习刚体的定轴转动运动学。

刚体做定轴转动时，如图3-2所示，刚体上任一点P将在通过点P且与转轴垂直的平面内做圆周运动，该平面称为转动平面，圆心O是转轴与该平面的交点。因此，刚体的定轴转动实质上就是刚体上各个点在垂直于转动轴的平面内的圆周运动。

显然，刚体做定轴转动时，在相同的一段时间内，刚体上转动半径不同的各点，其位移、速度、加速度一般各不相同，但各点的半径扫过的角度却是相同的，而且角速度和角加速度也是相同的。因此用角量来描述刚体的定轴转动是较为方便的。我们以前讨论过的角位移、角速度和角加速度等概念以及有关公式对刚体的定轴转动都适用，即刚体的角速度为

角速度ω可以定义为矢量，用ω表示。它的方向规定为沿转轴的方向，指向与刚体转动方向之间的关系按右手螺旋法则确定，如图3-3所示。

刚体的角加速度为

离转轴的距离为r的质元的线速度和刚体的角速度的关系为

v=rω

加速度与刚体的角加速度和角速度的关系为

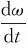当刚体绕定轴转动时，如果在任意的时间间隔Δt内，角速度的增量都相等，这种变速转动就是匀变速转动。匀变速转动的角加速度α为一恒量。用ω0表示刚体在t=0时刻的角速度，用ω表示刚体在t时刻的角速度，用θ表示刚体从0到t时刻这段时间内的角位移，仿照匀变速直线运动公式的推导，由式ω=和式α=可得匀变速转动的相应公式为

ω=ω₀+αt

ω₂-ω²₀=2αθ

例3-1　一飞轮转过的角度和时间的关系为θ=at+bt³-ct⁴，式中a、b、c都是常量。求它的角加速度。

解　将θ=at+bt³-ct⁴对时间t求导，即得飞轮角速度的表达式为(www.daowen.com)

角加速度是角速度对时间t的导数，因此得

由此可见，飞轮做的是变速转动。

例3-2　一飞轮半径为0.2m，转速为150r/min，因受到制动而均匀减速，经过30s停止转动。求：

（1）角加速度和此时间内飞轮转过的圈数；

（2）制动开始后t=6s时飞轮的角速度；

（3）t=6s时飞轮边缘上一点的线速度、切向加速度和法向加速度。

解　（1）由题意知：

当t=30s时，ω=0。因飞轮做匀减速转动，由式（3-3）可得

上式中“-”号表示α的方向与ω0的方向相反，而飞轮在30s内转过的角度为

于是，飞轮共转了

（2）在t=6s时，飞轮的角速度为

（3）在t=6s时，飞轮边缘上一点的线速度大小为

v=rω=0.2×4π=2.5m/s

切向和法向加速度为

a_n=rω²=0.2×（4π）²=31.6m/s²