§2-3　动量定理　动量守恒定律

本节研究力的时间积累效应。在引入冲量和动量的基础上，讨论动量定理和动量守恒定律。

一、冲量　质点的动量定理

牛顿当初建立的牛顿第二定律，并不是以F=ma的形式给出的。他所选择的形式为

并且认为mυ为一独立的物理量。如果引入p=mυ，上式可写为

将式（2-21）写成

Fdt=dp=d（mυ）

两边积分得

∫^t₀Fdt=∫^p_p0dp=p-p₀=mυ-mυ₀

式（2-22）表明力对时间的积累效应，使物体的mυ发生了变化。正如牛顿所言，物理量p=mυ是不能由质点的质量m和速度υ的分离值所能取代的独立物理量，mυ称为动量。动量是一个矢量，其方向和速度相同，动量也是相对量，与参考系的选择有关。在SI单位制中动量的单位为kg·m/s。令I=∫^t_t0Fdt，称为时间间隔t₀→t内作用在质点上的力的冲量，则（2-22）式可写成

I=p-p₀

冲量I是矢量，它的方向和动量增量的方向相同。式（2-23）表明在给定的时间内，作用于物体上的合外力的冲量，等于物体在该时间内动量的增量。这便是质点的动量定理。式（2-22）在直角坐标系的分量形式为

由式（2-22）可以看出，如果物体间的相互作用时间间隔很短，即t-t₀很小，而动量却发生了有限的变化，即mυ-mυ₀很大，则这时的相互作用力F必很大，这种力常称为冲力。冲力和时间的关系，一般不易精确给出，常可用如图2-20表示，图中曲线下的面积等于力的冲量I的大小（或动量的增量），由∫^t_t0Fdt决定，和冲力F与时间t的依赖关系的细节无关。因此，常用平均冲力F—来表示，即

如果物体间的相互作用力F有限，相互作用时间t-t₀很短，则冲量I很小，于是p（t）-p（t₀）也很小，物体的动量或运动状态可以近似地认为没有发生变化。冲力在生产实践中有广泛的应用。

例2-11　如图2-21所示，一质量m=0.2kg的小球，以v₀=8.0m/s的初速度沿与地面法线成α=30°角的方向射向水平地面，然后沿与法线成β=60°角的方向弹起，碰撞时间Δt=0.01s。设地面光滑，摩擦不计。求小球给地面的平均冲力。

解　选小球为研究对象，当小球和地面相互碰撞时，地面给小球反冲力使小球弹起。因地面光滑，摩擦不计，地面给小球的冲力沿地面法线方向，在碰撞时间Δt内迅速变化，用平均反冲力F代替，方向竖直向上；小球所受重力mg，方向向下。小球的初动量为mυ₀，与法线成α角，设小球的末速度为υ，则其末动量为mυ，与法线成β角。小球和地面的碰撞过程中所受合力为：F+mg，因F与mg方向相反，所以合力的大小为

︳F+mg︳=F-mg

根据动量定理

（F+mg）Δt=mυ-mυ₀

本题可用两种解法。

解法一：直接用矢量作图法求解。矢量mυ、mυ₀、（F+mg）Δt组成矢量三角形，如图2-22所示。因α+β=90°，这是一个直角三角形，所以

代入数据，得

F=186.5N

由牛顿第三定律，小球给地面的平均冲力为

F′=F=186.5N

F′的方向竖直向下。由这个结果可以得出，如果碰撞时间Δt很短，重力mg和平均冲力F′相比较小，按本例的数据，忽略重力，将只会引起1%的误差，因此通常情况下，忽略重力是允许的。

在一般的碰撞、冲击、爆炸等问题中，作用时间极短，这时作用在物体上的其他外力（例如重力）和冲力相比往往可以忽略。

解法二：用动量定理的投影式求解。因小球在竖直平面内运动，取坐标轴如图2-22所示，根据动量定理的投影式有

x方向：

0=mvsinβ-mv₀sinα(www.daowen.com)

y方向：

（F-mg）Δt=mvcosβ-（-mv₀cosα）

联立以上二式，消去v，得

因α+β=90°，sin（α+β）=1，sinβ=cosα，故有

代入数据可求得与解法一同样的结果。

二、质点系的动量定理

设所研究质点系中，各质点间存在相互作用力。现考察第i个质点的受力情况。设系统内第j个质点对i质点的作用力为f_ij，则i质点所受内力为

若设质点i所受外力为F_i，质点i受合力为F_i+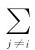f_ij，对质点i运用动量定理有

现对质点系运用动量定理，则有

其中，在对i求和的过程中，由于内力总是成对出现，每对内力都等值反向，因此

则有

式（2-27）是质点系动量定理的数学表述，即质点系总动量的增量等于作用于该系统上合外力的冲量。这表明系统的内力不会改变系统的总动量，和质点系的动能定理不同，内力作用一般会改变系统的总能量。从式（2-26）看出，在系统内部动量的传递和交换中，是内力承担作用。

三、动量守恒定律

如果式（2-27）中∑F_i=0，则有

即

表述为：当系统所受合外力为零时，系统的总动量保持不变。这就是动量守恒定律。

动量守恒定律在直角坐标系中的分量式为

∑F_x=0，p_x=∑m_iv_ix=恒量

∑F_y=0，p_y=∑m_iv_iy=恒量

∑F_z=0，p_z=∑m_iv_iz=恒量

这就是说，当系统所受合外力在某一方向上的分量为零，则系统在该方向上的动量分量守恒。此外，在有些相互作用，如碰撞、打击、爆炸问题中，系统所受合外力并不为零，但外力与系统内力相比较，外力对系统动量变化的影响很小，可以忽略不计，可近似认为系统动量是守恒的。

由于动量是相对量，所以运用动量守恒定律时，必须把各质点的动量统一到同一惯性坐标系中。

虽然，在讨论动量守恒定律的过程中，从牛顿第二定律出发，并运用了牛顿第三定律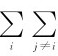（f_ij=0），但动量守恒定律是比牛顿定律更为普遍的规律，它是物理学中最普遍、最基本的原理之一。迄今为止，不论是在宏观世界还是微观世界，尚未发现动量守恒有任何例外。守恒定律不论在理论的研究中，还是在实际的应用中，都有着巨大的作用。如1930年奥地利物理学家泡利（W.Pauli，1900—1958）利用动量守恒提出中微子假设，于1953年得到实验证实。在实用上，当今航天事业的发展，把航天器送入太空的火箭，正是利用动量守恒的原理设计的。

例2-12　用皮带传送煤，皮带由电动机牵引，以v=1.5m/s的速率匀速前进，料斗中的煤粉以qm=20kg/s的卸煤量连续不断地向皮带送料。求电动机的牵引力。

解　因煤粉连续不断地落到皮带上，考虑其中的一个时间间隔Δt，在Δt开始的时刻，设皮带上已有煤粉质量为m，而在Δt时间内落到皮带上的煤粉质量为Δm，取皮带质量为M，这样，皮带、质量为m的煤粉和质量为Δm的煤粉三者作为一个系统。在开始时刻t, M、m的初速度为v，Δm的水平初速度为0，在（t+Δt）时刻，M、m的末速度仍为v，Δm的末速度也为v，系统所受的外力即电动机的牵引力为F, F和v都是水平方向，在水平方向用质点组的动量定理有

FΔt=（M+m+Δm）v-（M+m）v=Δmv

故

式中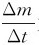，为料斗的卸煤量qm，所以有

F=qmv=20×1.5=30N