一、惯性定律惯性参考系
300多年前，意大利的物理学家伽利略注意到，当一个小球在斜面上向下滚动时，其速度越来越大，而向上滚动时，其速度越来越小。由此他推断，当小球沿水平面滚动时，其速度应当不变。实际上，在水平面上小球会越滚速度越小，直至停止。伽利略认为，小球停止是由于摩擦力和空气阻力的缘故，静止并非是小球的“自然状态”。他还观察到，表面越光滑，小球便会滚动得越远。于是，他推论得出：若没有摩擦力和任何阻力，小球将永远滚动下去。他通过抽象思维，逻辑地论断：力不是维持物体运动的原因，而是运动状态改变的原因。
牛顿继承和发展了伽利略的见解，首次以概括性的语言写到：
任何物体都要保持其静止或匀速直线运动状态，直到外力迫使它改变运动状态为止。这便是通常所说的牛顿第一定律。不受任何外力的物体可视为孤立质点。故牛顿第一定律也可表述为：一个孤立质点将永远保持其原来静止或匀速直线运动状态。
牛顿第一定律表明，任何物体都具有保持其运动状态不变的性质，这个性质叫做惯性，惯性是物体的固有属性。所以，牛顿第一定律也称为惯性定律。在自然界中，不存在真正的孤立物体。因此，惯性定律不能通过实验直接验证。
我们曾指出，描述物体的运动必须选定参考系。惯性定律严格成立的参考系，即在这个参考系中，当物体不受其他物体的作用时，必保持静止或匀速直线运动状态，这个参考系就称为惯性参考系。显然，相对惯性系以恒定速度运动的参考系也是惯性系；然而，相对惯性系做加速运动的参考系，则是非惯性系。
严格地说，在自然界中不存在惯性系。在研究物体运动时，常选地球或太阳作为惯性系，其实它们都不是真正的惯性系。因为地球绕太阳公转的向心加速度约为5.9×10-3m/s2，其自转形成的加速度可达3.4×10-2m/s2，而太阳仍以约3×10-10m/s2的向心加速度随银河系旋转。尽管如此，对大多数精度要求不很高的实验，上述效应可以忽略，地球可以认为是近似程度相当好的惯性系，太阳则是比地球更好的惯性系。
二、牛顿第二定律惯性质量和引力质量
惯性定律是指一个不受任何外力的质点在惯性参考系中的行为，这只能是一个孤立质点，没有任何其他物体存在的情况。现在我们讨论物体间相互作用的规律，牛顿第二定律指出：物体受到外力作用时，它所获得的加速度a的大小与合外力的大小成正比，与物体的质量成反比；加速度a的方向与合外力F的方向相同。其数学表述为
F=kma
比例系数k与单位制有关，在国际单位制（SI）中k=1。
牛顿第一定律表明任何物体都有惯性，但没有给出惯性的量度。牛顿第二定律表明：相同的外力作用在不同的物体上，质量大的物体获得的加速度小；质量小的物体获得的加速度大。这意味着质量的大小，决定着物体运动状态改变的难易程度。因此，质量就是惯性大小的量度。牛顿第二定律中的质量常被称为惯性质量。
牛顿继承前人有关观测天体的研究成果，进一步深入研究提出：任意两个物体之间都存在引力作用，引力的大小与两个物体质量的乘积成正比，与两物体之间的距离的平方成反比。这一规律称为万有引力定律。其数学形式为
式中，G=6.67428×10-11N·m2/kg2，称为引力常量；r为两质点间的距离；r0为m2对m1的单位位置矢量；负号表示m1对m2的引力方向总是与m2对m1的矢径的方向相反；m1、m2称为引力质量。
实验证明，引力质量等于惯性质量。因此，我们以后在经典力学的讨论中不再区分引力质量与惯性质量。引力质量与惯性质量等价是广义相对论的基本出发点之一。
三、牛顿第三定律
牛顿第三定律表明物体间相互作用的性质。两个物体之间的作用力F和反作用力F′，沿同一直线，大小相等，方向相反，分别作用在两个物体上。这就是牛顿第三定律，其数学表述为
运用牛顿第三定律分析物体的受力情况时必须注意：作用力和反作用力互为依存，同时产生，同时消灭，任何一方都不可能孤立地存在；它们分别作用在两个物体上；它们属于同种性质的力。如果作用力是万有引力，反作用力也一定是万有引力；作用力是摩擦力，反作用力也一定是摩擦力；作用力是弹性力，反作用力也一定是弹性力。
四、牛顿运动定律的应用举例
牛顿运动定律的研究对象是质点模型，只在惯性参考系中成立。在具体问题中，物体的运动情况比较复杂，所研究物体和其他物体相互联系着，物体各部分之间有相对位移。应用牛顿定律研究它们时，需要把它们各自隔离开来，这是应用牛顿定律分析和解决具体问题时常用的方法，称为隔离体法。求解质点动力学问题可以归纳为两类：一类是已知物体的受力情况，由牛顿定律求解物体的运动状态；另一类是已知物体的运动情况，求作用于物体上的力。第一类问题代表着一种纯粹的演绎过程，它是对物理学问题和工程学问题作出分析和设计的基础；第二类问题则包含着力学的归纳性和探索性的应用，这是发现新定律的一个重要途径，如牛顿的万有引力定律正是利用开普勒的运动定律导出的。
具体应用牛顿定律解题时，首先要根据题意确定研究对象，正确分析它的受力情况和运动情况，按照牛顿第二定律列出运动方程求解。下面我们给出一些例子来说明如何运用牛顿定律正确分析和解题的方法。
例2-1 如图2-1所示，用一细绳跨过定滑轮，在绳的两端悬挂质量为m和M的物体。设滑轮和绳子的质量可以忽略不计，绳子和滑轮间没有相对滑动。求两物体运动的加速度及物体对绳子的拉力。
解 选地面作为惯性参考系，把整个系统分成三部分：m、M和绳子，受力分析如图2-1所示。
对m：它受到两个力，重力mg和绳子的拉力T1。设所求的加速度为a，方向向上，根据牛顿第二定律，有
T1-mg=ma
对M：同理有
Mg-T2=Ma
对绳子：绳子受到两个力，分别为m和M给绳子的拉力T1′和T2′（T1和T2的反作用力），由于绳子的质量可忽略，因此根据牛顿第二定律有
T2′-T1′=0
即
T1′=T2′
联立以上各式，解得
例2-2 如图2-2所示，一质量为m=50kg的物体放在水平地面上，受到与水平方向成θ=60°仰角的拉力F作用而沿水平地面滑动，物体和地面间的动摩擦因数为μ=0.20。欲使物体匀速运动，拉力F应为多大?物体对地面的正压力为多大?
解 选物体为研究对象，以地面为惯性参考系。物体受到四个力：重力mg，方向向下；地面的支撑力N，方向竖直向上；拉力F，方向斜向右上方和水平方向成θ角；滑动摩擦力f，方向水平向左和运动方向相反。
在质点动力学问题中，只研究物体的平动，可把问题简化为一个质点，从而把物体所受各个力作用点平移集中到一点，这样便于力的合成与分解。因四个力同在一个平面内，故可以建立平面坐标系Oxy（如图2-3所示），用牛顿第二定律的投影式来解决问题比较方便。
物体所受沿x方向的各力的合力为
Fx=Fcosθ-f
物体沿x方向做匀速运动，根据牛顿第二定律，沿x方向的投影式Fx=max，则本题可列方程如下：
Fcosθ-f=0
物体所受沿y方向的各力的合力为
Fy=Fsinθ+N-mg
物体沿y方向没有运动，ay=0，根据Fy=may，有
Fsinθ+N-mg=0
式（1）、（2）是两个独立的方程，其中包含三个未知的力F、N、f。因此，必须再找出一个独立的方程才能求解，这个独立的方程就是滑动摩擦力f和正压力N之间的关系。(www.daowen.com)
f=μN
联立式（1）、（2）、（3），求解得
代入已知数据得物体匀速运动所需拉力为
F=146N
欲求物体对地面的正压力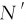
，它的大小等于地面对物体的支撑力N的反作用力的大小，根据牛顿第二定律有
N′=-N
因而
负号表示N′的方向垂直于水平地面向下。
例2-3 如图2-4所示，水平桌面上放一三角形楔块B，楔块的斜面是光滑的，斜面上放有质量为m的重物A，楔块的质量为M，楔角为θ，楔块和水平桌面之间的动摩擦因数为μ。今以水平力F推楔块，欲使重物A在楔块B上无相对滑动，而随楔块一起前进，水平推力F应为多大?这时重物A对楔块的压力为多大?
解 因斜面光滑，若无推力F, A将沿斜面下滑，若推力F过大，A又会沿斜面上升，所以F应有合适的大小才能使A和B无相对滑动而一起运动。这时可把A和B看成一个整体，即当做一个质点。设物体加速度为a，受力如图2-5所示。取坐标系Oxy，根据牛顿第二定律，列出如下方程。
x方向：
F-f=（m+M）a
y方向：
N-（m+M）g=0
因楔块B在水平桌面上滑动，f为滑动摩擦力，有
f=μN
式（1）、（2）、（3）中有四个未知量F、f、N、a，要求出结果，还必须再找出一个方程。在本题中，A、B间无相对滑动是有条件的，要找的这个方程应反映这个条件。为此，把A单独作为研究对象，它受到B对它的作用力N1，因B的斜面光滑，N1的方向应垂直于斜面向上，此外，A还受到重力mg（图2-6）。根据A、B一起运动的条件，A和B必须有相同的加速度，列出A的牛顿第二定律投影式方程。
x方向：
N1sinθ=ma
y方向：
N1cosθ-mg=0
虽然现在又多出一个未知量N1，但也多出了一个方程，因此，联立式（1）、（2）、（3）、（4）、（5），求解得
a=gtanθ
F=（m+M）g（μ+tanθ）
A对B的正压力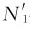
与N1的大小相等，即
解 本题也可分别取A、B为研究对象，各自画出它们隔离体的受力图。A的牛顿第二定律的投影式为式（4）、（5）；B的牛顿第二定律的投影式如下。
x方向：
F-f-N1′sinθ=Ma
y方向：
N-Mg-N1′cosθ=0
再加上式（3）和牛顿第三定律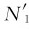
=N1，此时方程数目和未知数数目均为六个，联立即可求解，所得结果和上面相同。
例2-4 如图2-7所示，长为l的细绳上端固定，下端系一质量为m的小球，当小球沿水平圆周以角速度ω匀速转动时，细绳画出一圆锥面，因此，这种摆称为圆锥摆。求此时细绳和竖直方向间的夹角θ。
解 选小球m为研究对象，它受到细绳对它的拉力T和重力mg，因小球在水平面内做圆周运动，因此它的加速度a必在该平面内。按照牛顿第二定律，它所受合力T+mg的方向应和a的方向一致。故在任一时刻，mg、T、a三者必处在同一竖直平面内，为此建立一个和地面相联系的惯性坐标系，坐标系原点和某瞬时小球m所在位置重合，y轴竖直向上，x轴水平指向圆周的圆心，如图2-8所示。根据牛顿第二定律的投影式有
x方向：
Tsinθ=ma
y方向：
Tcosθ-mg=0
因小球在竖直方向无运动，故式（2）右边为零，a为小球做匀速率圆周运动的向心加速度，有
a=rω2=（lsinθ）ω2
联立式（1）、（2）、（3），求解得
由这个结果可知，当l、ω一定时，θ是确定的。对一定的l，随ω的增大，θ角增大；当ω→∞时，θ→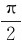
，细绳近乎于水平位置；当ω→0时，cosθ→∞，这结果显然不合理，所以上面的结果只能在ω＞
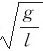的条件下适用。
利用圆锥摆的原理可以制成离心节速器和离心分离器。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
