§1-3 几种典型运动的描述
一、抛体运动
在地面附近,重力加速度可看成常矢量g,如果再忽视空气阻力,将使问题大为简化。我们取直角坐标系如图1-5所示,x轴和y轴分别沿水平和竖直方向,设抛体的初速度为v0,它和x轴的夹角为α。显然,抛体的运动沿x轴是匀速运动,而沿y轴方向以加速度-g做匀加速运动。初速度v0的两个分量分别为v0x=v0cosα和v0y=v0sinα,根据匀速运动和上抛运动的规律,在任何时刻t,抛体运动速度的分量为
抛体运动在t时刻的位置坐标:
由上式消去t,得轨迹方程:
这就是抛物线方程。由式(1-17)和(1-18)可求出抛体所能达到的最远点,称为射程,它由特征y=0得到。在y=0时,t=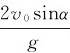 ,所以有
,所以有
也可求出抛体到达的最大高度,称为射高,它由特征vy=0得到。在vy=0时t=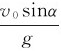 所以有
所以有
还可以求出飞行时间T(落到抛出点高度所用的时间):
从式(1-20)可以看出,当α=45°时,有最大射程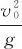 。上述由式(1-20)、(1-21)、(1-22)给出的公式称为弹道学基本关系。应当指出,这是在忽略空气阻力的情况下得到的,只有在v0比较小的情况下,它们才比较符合实际,实际子弹或炮弹在空气中的飞行规律和以上公式有较大的差异,因为一般子弹的v0较大,空气阻力不可忽略。
。上述由式(1-20)、(1-21)、(1-22)给出的公式称为弹道学基本关系。应当指出,这是在忽略空气阻力的情况下得到的,只有在v0比较小的情况下,它们才比较符合实际,实际子弹或炮弹在空气中的飞行规律和以上公式有较大的差异,因为一般子弹的v0较大,空气阻力不可忽略。
二、切向加速度和法向加速度
当物体做曲线运动时,运动轨道如图1-6(a)所示,t时刻质点在P点的速度为υ1,t+Δt时刻质点运动到Q点,速度为υ2,在Δt时间内速度增量为Δυ。图1-6(b)给出了υ1、υ2、Δυ三者间的关系。图中矢量BC就是Δυ。如果在AC上截取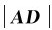 =
=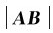 =
=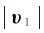 ,则剩下的部分:
,则剩下的部分:
式中,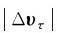 体现了速度大小的增量。连接BD记为Δυn,其反映了速度方向的增量。因此,速度增量Δυ=Δυ+Δυn,表明了速度大小和速度方向两方面增量的意义。由图1-6(b)不难看出,当Δt→0时,Δθ→0,则∠ABD→
体现了速度大小的增量。连接BD记为Δυn,其反映了速度方向的增量。因此,速度增量Δυ=Δυ+Δυn,表明了速度大小和速度方向两方面增量的意义。由图1-6(b)不难看出,当Δt→0时,Δθ→0,则∠ABD→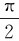 ,在极限条件下,Δυn的方向垂直过P点的切线,即沿曲线在P点的法线方向;同时,在Δθ→0的极限条件下,
,在极限条件下,Δυn的方向垂直过P点的切线,即沿曲线在P点的法线方向;同时,在Δθ→0的极限条件下,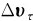 的方向就是υ1的方向,即P点的切线方向。
的方向就是υ1的方向,即P点的切线方向。
︳Δυn ︳≈υΔθ,在Δθ→0时,dυn=υdθ,若以n0表示P点的法线方向的单位矢量,以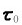 表示P点切线方向(指向质点前进方向)的单位矢量,则
表示P点切线方向(指向质点前进方向)的单位矢量,则
由于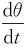 =
=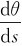 ·
·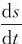 =v·
=v·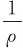 ,式中ρ为过P点的曲率圆的曲率半径,则上式可表示为
,式中ρ为过P点的曲率圆的曲率半径,则上式可表示为
式中,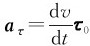 ,
,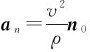 分别为加速度的切向分量和法向分量,分别称为切向加速度和法向加速度,它们各自反映速度的大小和方向的变化。加速度的大小可表示为
分别为加速度的切向分量和法向分量,分别称为切向加速度和法向加速度,它们各自反映速度的大小和方向的变化。加速度的大小可表示为
三、圆周运动
质点做圆周运动时,其轨道曲率半径就是圆的半径,处处相等,速度的方向始终在圆的切线上。因此描述圆周运动时,通常采用平面自然坐标系和平面极坐标系,分别进行线量和角量的描述,现给以简单讨论。
在质点运动的轨迹上,以运动的质点为坐标原点,一坐标轴沿轨迹在该点的切线指向质点前进的方向,另一坐标轴沿该点轨迹的法线指向轨迹曲率中心方向。这样的坐标系称为自然坐标系。在自然坐标系中,位置矢量r是路径s的函数r(s),如图1-7所示,取质点路径s上一点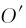 为原点,
为原点,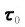 和n0分别为切向单位矢量和法向单位矢量。由于
和n0分别为切向单位矢量和法向单位矢量。由于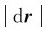 =ds,在自然坐标系中位移、速度可分别表示为
=ds,在自然坐标系中位移、速度可分别表示为
由式(1-24)可知,圆周运动的切向加速度和法向加速度为
式中,R是圆的半径。由此看出,所谓匀速率圆周运动就是切向加速度等于零的圆周运动,即在任何相等的时间内,沿圆弧走过相等的弧长,其速率保持不变,但其方向不断改变的圆周运动。
质点做圆周运动时,还常用平面极坐标系来描述。我们知道在平面直角坐标系中,若质点做曲线运动,如图1-8所示,在某一时刻t位于A点,它的位置可由直角坐标(x, y)确定,也可以用从O点到A点的有向线段r和它与x轴的夹角θ确定,即用(r,θ)来确定。这种以(r,θ)为坐标的坐标系称为平面极坐标系。这时,O点称为极点,Ox轴称为极轴,r称为极矢,θ称为极角。点A的位置坐标在这两种坐标系的关系为
x=rcosθ
y=rsinθ
若质点在Oxy平面上以半径为r做圆周运动,某一时刻它位于A点,在平面极坐标系中它的极矢为r, r和极轴Ox之间的夹角为θ,在t+Δt时刻,质点运动到B点,极角为θ+Δθ。在Δt时间内,质点转过的角度为Δθ,称为质点的角位移。角位移既有大小又有方向,其方向约定:按右手螺旋规则,四指表示质点的旋转方向,拇指则表示角位移的方向。在图1-8中,质点沿逆时针方向转动时,角位移的方向为垂直纸面向外。应该指出,角位移虽然有大小和方向,但在质点做圆周运动时它只有正负之分。
我们用与引入速度和加速度同样的方法,定义极角θ(t)随时间的变化率,即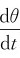 为角速度,用ω表示
为角速度,用ω表示
单位为弧度/秒(rad/s)。同样可以定义质点的角加速度β
单位为弧度/秒2(rad/s2)。质点做圆周运动,当角速度ω不随时间变化时,则为匀速率圆周运动,此时角加速度β=0。如角加速度β不随时间变化,但不等于0,则为匀加速圆周运动,对匀加速圆周运动用与研究匀变速直线运动相同的方法可以得
其中,θ0和ω0分别表示t=0时刻的角位置和角速度。如图1-8所示,在Δt时间内角位移Δθ,相应地,质点在圆周轨道上经历的路程Δs=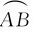 =rΔθ。容易证明,在圆周运动中,用极坐标系描述圆周运动的角量和用自然坐标系描述圆周运动的线量之间有如下关系:
=rΔθ。容易证明,在圆周运动中,用极坐标系描述圆周运动的角量和用自然坐标系描述圆周运动的线量之间有如下关系:
例1-2 我国神舟六号飞船于2026年10月12日升空,在绕地球5圈后变轨为距地面343km的圆轨道,飞船每90min环绕地球飞行一圈。求飞船的速率和向心加速度。(地球半径为6.37×103km)
解 飞船圆轨道的半径为
R=343+6.37×103=6.713×103km=6.713×106m
飞船的速率为
飞船的向心加速度的大小为
四、一般平面曲线运动
如图1-9所示,质点沿轨迹LN做一般平面曲线运动,不难证明,质点在任一位置A点的加速度a也可分解为两个分量:法向加速度an和切向加速度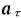 ,且有
,且有
式中,en和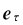 为沿轨迹曲线上A点法线方向和切线方向的单位矢量,ρ为轨迹曲线在A点的曲率半径。
为沿轨迹曲线上A点法线方向和切线方向的单位矢量,ρ为轨迹曲线在A点的曲率半径。
与圆周运动不同,一般平面曲线上不同点处的曲率半径和曲率中心是不同的,质点在任一点处法向加速度的大小与质点在该处的速率平方成正比,与该处的曲率半径成反比,方向沿该处曲率圆的半径指向曲率中心。
一般平面曲线运动加速度的大小和方向可表示为
一般曲线运动中,法向加速度和圆周运动中的法向加速度相似,只反映速度方向的变化;切向加速度则和直线运动中的加速度相似,只反映速度大小的变化。质点做圆周运动时,曲率半径不变,曲率中心为圆心,可见圆周运动是一般曲线运动的特殊情况。
例1-3 一质点以v=A+Bt的速率从t=0开始由P点绕圆心做半径为R的圆周运动,其中A、B均为常量,求质点沿圆周运动一周时的速度和加速度。
解 由题意知质点的速率
v=A+Bt
t=0时,v0=A。质点的切向加速度
说明质点做匀加速圆周运动。
当质点从初始位置出发运动一周后回到原处,由匀加速运动的速度公式
其大小v=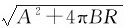 ,方向沿切线指向前进方向。
,方向沿切线指向前进方向。
此时质点的法向加速度为(https://www.daowen.com)
如图1-10所示,质点加速度
加速度的大小为
方向为
综上所述,通过对上面几种典型的机械运动的描述,我们可以看出,运动学以矢量r(t),υ(t)及a(t)来描述质点的运动状态,而且还可以把运动分解为沿各个坐标轴方向的分运动,用位矢、速度和加速度在坐标轴上的投影式来描述质点的运动。
无论是用矢量法还是用投影法,都必须先选定参考系和坐标系,参考系的选择,由讨论问题的方便而定。在力学中常用直角坐标系和自然坐标系,位矢r(t)、速度υ(t)、加速度a(t)是运动学中的三个基本物理量,位矢r(t)是用来确定质点在空间相对于参考系位置的,随着质点的运动,位矢r(t)是随时间而变的,它是时间t的函数。该函数反映了质点的运动规律,称为质点的运动方程。速度υ(t)表征质点运动的快慢和方向,它以υ=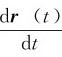 来量度,加速度以a=
来量度,加速度以a=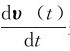 来量度。
来量度。
运动学的问题可以归纳为两类:
一类是已知运动方程,求运动状态,即已知r=r(t),求反映质点运动状态的υ(t)和a(t),这类问题是数学上的微分问题。
例1-4 一质点做曲线运动,其运动方程为r(t)= t2i+
t2i+ (2t+1)3/2j。求:
(2t+1)3/2j。求:
(1)质点在t=4s时的速度和加速度;
(2)质点在t=4s时的切向加速度和法向加速度。
解 (1)由υ=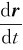 得
得
由a=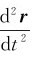 得
得
当t=4s时,
υ=4i+3j
所以,速度的大小为
其方向与x轴正方向的夹角为α,则
加速度a的大小为
其方向与x轴夹角为β,则
(2)由上面的速度υ的表示式可以求出任意时刻的速率为
所以任意时刻的切向加速为
t=4s时的法向加速度为
例1-5 已知质点沿双曲线xy=1运动,某瞬间,质点位于x1=1.2m处,0.36s后处于x2=1.40m。求质点的平均速度。
解 因为已知轨迹为xy=1,这个问题的关键是如何由轨迹求出Δr=Δxi+Δyj。由已知条件得
Δx=x2-x1=1.4-1.2=0.2m
由轨迹方程y= 得
得
Δy=y2-y1=-0.119m
根据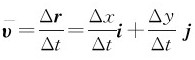 ,得
,得
所以有
另一类问题是已知质点的加速度(或速度)及运动的初始条件,求运动方程,这类问题在数学上是积分问题。
例1-6 一质点沿x轴做直线运动,已知其加速度a=-4tm/s2,在t=0时刻的初位置x0=5m,初速度v0=8m/s。求:
(1)质点各时刻的速度和位置的表达式;
(2)在t=1s、2s、4s时刻,质点的速度和位置。
解 (1)由a(t)=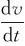 ,得
,得
dv=a(t)dt
对上式两边积分得
∫v(t)v0dv=∫t0a(t)dt
则
v(t)=v0+∫t0a(t)dt
所以
v(t)=v0+∫t0(-4t)dt=v0-2t2=8-2t2
同样,由v(t)=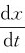 ,得
,得
dx=v(t)dt
对上式两边积分得
(2)当t=1s时,v=8-2=6(m/s)>0,质点向+x方向运动,有
当t=2s时,v=8-8=0,此时质点瞬时速度为0,有
当t=4s时,v=8-32=-24(m/s)<0,质点向-x方向运动,有
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





