一、位置矢量
为了确定质点的位置,首先我们选定参考系,然后在参考系上建立坐标系的原点和坐标轴。如图1-1所示,从原点O引一指向质点所在位置P的有向线段r=OP,这一矢量r叫做质点的位置矢量,简称位矢。位置矢量的大小为r,代表质点到原点O的距离;其方向标志质点的位置相对于O点的方位。在直角坐标系中,位置矢量r可用它沿三个坐标轴上的分量x、y、z表示为
r=xi+yj+zk
式中,i、j、k分别表示沿x、y、z三个轴正方向的单位矢量。位置矢量的大小r为
它的方向可以用r和x、y、z轴的夹角α、β、γ表示,这些角的余弦分别为
称为r的方向余弦。
在质点的机械运动过程中,它的空间位置矢量随时间改变,这种变化规律可以用矢量r的时间t的函数
r=r(t)
来表示,函数r(t)给出了任一时刻质点所在的位置,称为质点的运动方程。这时质点的坐标值x、y、z也是时间的函数,写为
称为运动方程的分量形式。知道了质点的运动方程,也就知道了质点的全部运动信息。力学的主要任务之一,正是依据所研究问题的物理条件,求解质点的运动方程。
质点运动在空间经历的路径,称为轨道。按质点运动轨道的形状,可分为直线运动和曲线运动。由式(1-3b)消去时间t,可得质点的轨道方程。式(1-3b)就是轨道以参数t为参量的参数方程。
运动方程和轨道方程的显然区别在于运动方程描述的是质点的位置随时间的变化过程,而轨道方程给出的是质点运动的空间结果,与时间无关。
例1-1 已知一质点的运动方程为r=ati+(b+ct2)j,其中,a、b、c为常数。求质点的轨道方程。
解 由运动方程知,在任意时刻t,该质点的坐标为
x=at
y=b+ct2
z=0
由(3)式可知,质点在Oxy平面内运动。由(1)式得
代入第二式即得
这就是该质点的轨迹方程,它是在Oxy平面内的抛物线。
二、位移矢量
位移的概念是为了描述质点的空间位置的变化而引入的。设质点沿图1-2中的曲线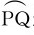 运动,在时刻t,质点位于P点,它的位置矢量是r(t),经过Δt时间后,t+Δt时刻到达Q点,其位置矢量为r(t+Δt)。为了求得质点在时间间隔Δt内位置变动的情况,只需从初位置P向末位置Q引一个矢量PQ,用它来表示质点位置变动的大小和方向,这个矢量叫做质点在给定时间间隔t→t+Δt内的位移矢量,简称位移,根据矢量加法的三角形规则有
运动,在时刻t,质点位于P点,它的位置矢量是r(t),经过Δt时间后,t+Δt时刻到达Q点,其位置矢量为r(t+Δt)。为了求得质点在时间间隔Δt内位置变动的情况,只需从初位置P向末位置Q引一个矢量PQ,用它来表示质点位置变动的大小和方向,这个矢量叫做质点在给定时间间隔t→t+Δt内的位移矢量,简称位移,根据矢量加法的三角形规则有
PQ=r(t+Δt)-r(t)=Δr
因而,质点在t→t+Δt时间间隔内的位移Δr等于质点在这段时间内位置矢量的增量。
位移不同于位置矢量,在质点的运动过程中,位置矢量表示质点某个时刻的位置,它描述了该时刻质点相对于坐标原点的位置状态,是描述状态的物理量;位移则表示某段时间内质点位置的变化,它描述这段时间内质点状态的变化,是与运动过程对应的物理量。位移也不同于质点所经历的路程,质点从P点运动到Q点所经历的路程Δs是图中从P到Q轨迹曲线的弧长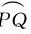 ,它和
,它和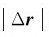 不相等,即Δs
不相等,即Δs ,只有当质点做单方向的直线运动时,Δs=
,只有当质点做单方向的直线运动时,Δs=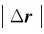 ,Δs表示质点实际走过的路程的长短,它是一个正的标量,只有当Δt→0时,Q点无限靠近P点,弦PQ和曲线
,Δs表示质点实际走过的路程的长短,它是一个正的标量,只有当Δt→0时,Q点无限靠近P点,弦PQ和曲线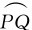 的长度Δs才相等,即
的长度Δs才相等,即
在直角坐标系中:
Δr=[x(t+Δt)-x(t)]i+[y(t+Δt)-y(t)]j+[z(t+Δt)-z(t)]k
=Δxi+Δyj+Δzk(www.daowen.com)
=(x2-x1)i+(y2-y1)j+(z2-z1)k
位移的大小为
Δr=(x2-x1)2+(y2-y1)2+(z2-z1)2
位移和路程的单位都是长度的单位,在国际单位制(SI制)中为m。
三、速度
位移矢量只说明了质点在某段时间内位置的变化,还不能充分说明质点的运动状态,为了说明质点运动的快慢程度,我们再引入速度的概念。在图1-2中,在t→t+Δt这段时间内,质点的位移为Δr,定义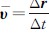 表示质点位置变化的方向和平均快慢,称为质点在这段时间内的平均速度,即
表示质点位置变化的方向和平均快慢,称为质点在这段时间内的平均速度,即
它的大小为 ,其方向和位移Δr的方向相同。实际上,质点在Δt时间内不同时刻的运动快慢和方向是不同的,因此平均速度只是一种粗略的描述方法。显然,时间Δt取得越短,近似程度就越好,平均速度就越能反映出t时刻的真实运动情况。当Δt→0时,
,其方向和位移Δr的方向相同。实际上,质点在Δt时间内不同时刻的运动快慢和方向是不同的,因此平均速度只是一种粗略的描述方法。显然,时间Δt取得越短,近似程度就越好,平均速度就越能反映出t时刻的真实运动情况。当Δt→0时, 趋近于一个极限矢量,这个极限矢量能确切地描述在t时刻质点运动的快慢和方向,因此我们把这个极限矢量定义为质点在t时刻的瞬时速度,简称速度,记做:
趋近于一个极限矢量,这个极限矢量能确切地描述在t时刻质点运动的快慢和方向,因此我们把这个极限矢量定义为质点在t时刻的瞬时速度,简称速度,记做:
质点在t时刻的速度,就是该时刻位置矢量随时间的变化率。速度的定义式(1-8)同时给出了速度的大小和方向。
速度是矢量,速度的方向由位移Δr的极限方向确定,如图1-3所示,当Δt→0时,Δr趋于轨道的切线方向,因此,质点在任一时刻的速度方向总是与该时刻质点所在处的轨道曲线相切,并指向前进方向。速度的方向反映了质点运动的方向。
描述质点运动时,我们也常采用称为速率的物理量。速率是标量,等于质点在单位时间内所经历的路程,而不考虑质点运动的方向。如图1-2所示,在Δt时间内质点所经历的路程为曲线 =Δs,则Δs与Δt的比值称为t时刻附近Δt时间内的平均速率,即
=Δs,则Δs与Δt的比值称为t时刻附近Δt时间内的平均速率,即
平均速率与平均速度的大小是不同的,例如,当质点绕行了一个闭合路径时,显然其位移为零,平均速度也为零,但是质点的平均速率不为零。但是当Δt→0时,曲线长度Δs与线段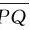 的长度
的长度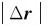 相等,瞬时速率为
相等,瞬时速率为
速度的大小 =v,即瞬时速率等于瞬时速度的模。所以质点在某一时刻的速率就是该时刻附近一个无限小的时间间隔内质点在单位时间内走过的路程,式(1-10)中的s=s(t)是质点运动轨道弧长的函数。因此,速率等于弧长随时间的变化率,速率直接反映了质点运动的快慢。
=v,即瞬时速率等于瞬时速度的模。所以质点在某一时刻的速率就是该时刻附近一个无限小的时间间隔内质点在单位时间内走过的路程,式(1-10)中的s=s(t)是质点运动轨道弧长的函数。因此,速率等于弧长随时间的变化率,速率直接反映了质点运动的快慢。
在直角坐标系中,速度υ可以分解为沿x、y、z三个坐标轴方向的分量形式
其中,vx=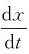 ,vy=
,vy=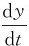 ,vz=
,vz=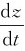 分别为质点沿x、y、z三个坐标轴方向的分速度,它们都是代数量,可正可负由于vx、vy、vz相互垂直,所以质点的速度的大小可表示为
分别为质点沿x、y、z三个坐标轴方向的分速度,它们都是代数量,可正可负由于vx、vy、vz相互垂直,所以质点的速度的大小可表示为
它的方向可由三个方向余弦决定:
速度和速率在量值上都是长度和时间之比,在国际单位制(SI)中其单位为m/s。
四、加速度
在力学中,位置矢量r和速度υ都是描述物体机械运动的状态参量,当一组参量(r,υ)已知后,质点的运动状态就确定了。现在我们引入加速度概念,它是用以描述速度矢量随时间的变化率的物理量。
在变速运动中,物体的速度是随时间变化的,这种变化可能是运动快慢的变化,也可能是运动方向的变化,一般情况下,速度的大小和方向都在变化。
设在时刻t,质点在P点,速度为υ(t),在t+Δt时刻,质点运动到Q点,其速度为υ(t+Δt),如图1-4所示,它表明在Δt这段时间内,速度的大小和方向都发生了变化。为了看清速度变化的情况,我们把图1-4中矢量υ(t+Δt)平移到P点。从矢量图看出,υ(t+Δt)和υ(t)的矢量差
Δυ=υ(t+Δt)-υ(t)
就是质点在Δt时间内速度的增量,它反映了质点在Δt时间内速度变化的情况。速度增量Δυ和时间间隔Δt的比值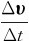 称为质点在Δt时间内的平均加速度
称为质点在Δt时间内的平均加速度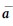 。即
。即
和平均速度相似,平均加速度也只是速度变化的一种粗略描述。要精确地描述,只有将Δt取得足够小。因此,把t→t+Δt时间内,当Δt→0时的平均加速度的极限定义为质点在t时刻的瞬时加速度,简称加速度。用a表示,即
按照这个定义,加速度a是速度υ对时间的一阶导数,其意义为速度υ对时间的变化率。加速度是矢量,它的大小描述质点在t时刻速度变化的快慢,它的方向是当Δt→0时,速度增量Δυ的极限方向,如图1-4所示。
在不同的速度变化中,Δυ的极限方向是不同的,因而a的方向也不同。例如,在直线运动中,加速度a的方向和速度υ的方向相同或相反,而在曲线运动中,加速度的方向和速度的方向并不相同,即加速度方向并不沿曲线的切线方向,而是指向轨道凹的一侧。
在直角坐标系中,加速度矢量也可以分解为沿x、y、z三坐标轴方向的分量
其中,ax=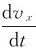 ,ay=
,ay=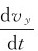 ,az=
,az= ,分别是沿x、y、z轴三个方向的分加速度,a的大小和方向由下式确定:
,分别是沿x、y、z轴三个方向的分加速度,a的大小和方向由下式确定:
在国际单位制中,加速度的单位是m/s2。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






