根据河流（河段）的特点和实际需要，选择环境需水量设计断面，将河流（河段）划分为若干小段，并将每一小段看作一个集水汇流区。先对各小段进行计算，最后求出整个河段的最小环境需水量。一般情况下，环境需水设计断面应选择在行政区的区界或有代表性的水质监测断面。

在一个设定的功能河段，如果选择某一断面作为控制断面（如图5.12 中j、k 断面），则其污染物的衰减曲线如图5.12中的A、B 所示。

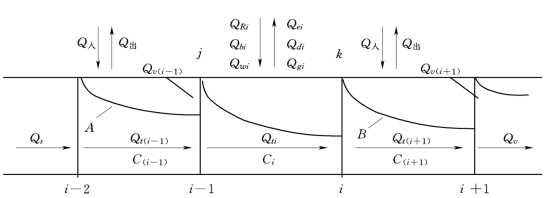
图5.12　功能区段划分及段首控制确定最小环境需水量示意图

A—第i－1 段浓度衰减曲线；B—第i＋1 段浓度衰减曲线；Ci—第i 段污染物浓度；Qv（i－1）—第i－1 断面的最小环境需水量；Qv（i＋1）—第i＋1 断面的最小环境需水量

一般情况下，河流在从源头流向河口的过程中，都是随着汇流面积的扩大而水量渐增。如果把河道水量表示成河流汇水面积或河流长度的函数的话，则水量是汇水面积或河长的单调递增函数或阶跃递增函数。如果设定了一个河道环境需水流量Qv，只要它是合理的、存在的（在数学上表示有解，在实际中表示在一定保证率下河流或河段存在这样的流量），则在ΔW＝0，废污水排放口的分布比较均匀的前提下，必定能沿着河流从源头找到一个对应的断面k，且k 断面以下的河道水量（Q），一般总能满足（Q）≥Qv。即只要计算出河流某一个断面环境需水量之后，其下游同一功能的河道流量一般总能满足河道环境功能流量的要求。按上述思路计算河道最小环境需水量的方法称为段首控制法（见图5.12）。段首控制的目的在于保证河流各功能区段内水量基本达到最小环境功能的要求。(www.daowen.com)

对于任一功能小段，Qvi必须同时满足下列方程

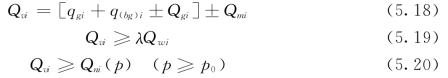
式中：Qvi为i 河段的河道生态需水量；qgi为河道上游来的地下水；q（bg）i为支流进入河道的地下水；Qgi为该河段本身进入河道的地下水来水，也就是该河段河道的基（础）流量；Qmi表示i 河段除河道基流外，为满足i 河段一定的河道生态与环境功能要求所必须具有的水量（详见3.4.1 节）；λ为河流稀释系数；Qwi为i 小段合理的污水排放总量（合理的污水排放量，是指达标排放的废污水量）；Qni（p）为不同水文年（如多年平均，枯水年，平水年）设定保证率（如p0＝p90，p0＝p80等）下i 小段的河道流量。

计算出所有断面的Qvi（i＝1，2，…，n，i 为断面数）后，即可确定整个河流（河段）的最小环境需水量。由于在确定每个断面的Qvi时，将每一小段看作一个闭合汇水区，因此，对其求和即可得到整个河流（河段）的最小环境需水量。

以河流稀释和自净作为主要环境功能的河道最小环境需水量的计算方法是结合目前我国水环境污染比较严重的具体情况提出的。随着废污水排放总量、污染物排放浓度、取水许可证等制度的实施，我国水环境状况会不断得到改善，河道环境需水的计算方法也会随之改变，并逐渐趋于成熟和完善。