早在19世纪初，Malthus［6］分别根据欧洲各国的人口资料分析发现，欧洲1790～1800年的平均人口增长率为0.30719，而19世纪的100年和20世纪前80年的人口平均增长率分别为0.266和0.137，进而Malthus指出区域人口的增长率将受到生产环境容量的限制，并提出以下的区域人口增长模式：

式中：xm 为区域资源所能承载的最大人口数，即目前我们称之为环境资源的人口承载力。

任何一个新兴城市（区域）的政府以及任何区域的客观生产环境和生活环境都不会允许本区域的劳动力无限地增长，所有的区域的地方政府都要根据区域对资金的消化能力、区域对劳动力的吸收、安置能力以及区域对生产的保障能力等制定适合本地区的人口政策。例如目前的深圳、香港的工资再高，银行利率再优惠也不可能把全国的劳动力都吸引过去。根据Malthus的模式式（1），提出以下的资源约束下的新兴城市劳动力（人口）增长模型：

式中：Nm 为在资源环境的约束下，该新兴城市（区域）所能承载或政府所规划的最大劳动力数；q 为劳动力的自然（人口）增长率；（s-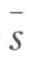）为该区域单位投资资本所能吸收的劳动力与外部平均单位投资资本所能吸收的劳动力的差；（w-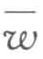）为该区域工资与外部平均工资的差异；c 为政府宏观控制劳动力增长修正系数；C为新兴城市（区域）劳动力的实际增长率。

由于资本K 的快速增长（积累）的后果，必定是伴随资本的外流，当外部的利率高于本区域利率时，或外部的投资环境比本区域的优越时，情况更是如此。因此，我们提出以下的投资环境约束下的新兴城市资本（经济）增长模型：(www.daowen.com)

式中：第一项表示有区域生产函数所控制的区域资本增长；第二项表示有区域资本因区域内外利率差异而导致的资本流动；第三项表示有区域资本因内外投资环境利率差异而导致的资本流动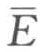，-E＞0 说明外部投资环境比该区域的好，区域资本将外流，反之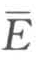，-E＜0 说明区域内的投资环境比外部的好，该区域将吸收外部的资本。

其中新兴城市（区域）的生产函数为：

式中：a、b 分别为资本增长指数和劳动力资源的增长指数。

式（2）、式（3）就是我们所提出的资源和投资环境约束下的新兴城市成长动力模式。