6．3．1．1　静电场表征模型

静电场数学建模基本原理是从水下电场满足的拉普拉斯方程出发，结合相应的边界条件，采用边界元等数值计算方法实现舰船水下静电场的模拟、仿真和预报。静电场数学建模方法主要包括边界元和等效源两种方法。边界元法计算过程中纳入了舰船尺度、结构等诸多参数，且具有较高的计算精度，在舰船防腐系统优化设计方面应用广泛；等效源法则是基于唯一性定理，利用偶极子或点电流源及其组合来等效模拟舰船目标静电场，对实测数据反演实现模型构建，相对于边界元等数值计算方法具有先验信息需求少、实时计算能力强的优点，并兼顾一定的模拟精度，常用于舰船电场空间换算和环境推演。

图6.2　海洋坐标系示意图

1）静电场边界元表征模型

假定海洋环境为空气-海水两层线性、均匀、各向同性媒质模型。建立直角坐标系（图6.2），x Oy平面与空气-海水交界面重合，z轴垂直向下。

舰船与腐蚀相关电场的电位u满足拉普拉斯方程：

边界条件为

其中n为边界外法线方向，jn为电流密度法向分量，与电位u存在如下关系：

式中　σ——海水电导率；

Ω——海水电解质区域；

S1——船体浸水部分涂层完好表面；

S2——涂层破损表面；

S3——牺牲阳极表面；

S4——辅助阳极表面；

Sw——海水-空气交界面；

S∞——无穷边界。

通过三维格林公式，将上述微分方程转化为积分方程，则空间内部Ω和边界上任一点Γs电位值up可用边界上函数u及其电流密度法向分量的曲面积分表示：

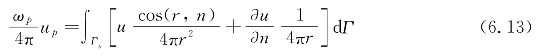
式中　ωp——p点对区域Ω的立体角。

当p点在Ω内部时，有ωp=4π，这时，

式中　Γs——船体浸水部分表面和无穷包络面总和；

n——边界Γs的外法线方向。

式（6.13）是边界积分方程，该方程建立了边界Γs上的u与其法向导数的关系。由于边界Γs上S1、S2、S3面u与满足金属材料极化方程，S4、Sw、S∞上为定值，因此可用边界单元法解出边界Γs上未知的u和来。然后将u和代入式（6.14），即可计算区域Ω任一点p的u。

利用边界元法求解积分方程（6.13）。首先将边界Γs剖分成若干个单元Γe，然后在各单元上插值，则式（6.13）中的边界积分可分解为诸单元积分之和，对于单元节点i，式（6.13）可写为

边界元法中，单元插值可分为零次插值、线性插值和二次插值三种。式（6.16）可转换为下列矩阵方程：

(www.daowen.com)

结合边界条件式（6.11），求解方程（6.17），便可计算出各节点的u和将u和代入式（6.14），便可计算空间中的电位u，利用数值差分可计算出空间电场强度Ex、Ey、Ez。

2）静电场等效源表征模型

前面提到等效源法一般包括点电流源和偶极子模型，在这里以偶极子阵列模型为例，给出舰船水下电场的等效源表征模型。

通常偶极子以均匀间距布置在舰船艏艉中心线上或两侧。为了便于描述舰船腐蚀相关电场，规定如下坐标系：x Oy平面与空气-海水界面重合，x轴平行于舰船艏艉中心线方向，指向船艏为正，称为纵向；y轴垂直于艏艉中心线方向，以指向右舷为正；z轴垂直于海平面，以向下为正，称为垂直方向。

假设在舰船水下部分布放n个x方向水平电偶极子，其坐标分别为（），电偶矩分别为Pxj，则每个水平电偶极子在海水中点Si（xi，yi，zi）产生的电场为

式中　m——测点个数；

aij——单位电偶矩的第j个水平电偶极子在第i个测点Si（xi，yi，zi）产生的电场纵向分量；

bij——单位电偶矩的第j个水平电偶极子在第i个测点Si（xi，yi，zi）产生的电场横向分量；

cij——单位电偶矩的第j个水平电偶极子在第i个测点Si（xi，yi，zi）产生的电场垂直分量。

将线性方程组（6.18）写成矩阵形式：

令M=3m，N=n，则d为M×1维向量，称为观测数据向量；G为M×N阶矩阵，称为数据核矩阵；m为N×1维向量，称为模型参数向量。

式（6.19）是舰船腐蚀相关电场电偶极子模型的矩阵方程，由矩阵代数便可求出式（6.19）的解。由于舰船腐蚀相关电场建模中，观测数据向量的长度通常大于模型向量长度，因此式（6.19）一般为超定方程，存在最小二乘解：

由式（6.23）计算偶极子电偶矩后，便可利用式（6.18）计算其他测点的舰船腐蚀相关电场值，实现测量数据的深度和距离换算。

6．3．1．2　静磁场表征模型

静磁场建模研究过程至今已经经过了几十年，其中出现了很多经典模型，包括拉普拉斯方程解算法、旋转椭球体阵列算法、偶极子阵列算法、椭球体和偶极子混合阵列算法，随着计算机的发展还出现了有限元法和边界元法。对比上述方法，每种方法均有各自的优点和缺点，从物理意义上来讲，任何一种模型只要给予它充分的外部条件，它都可以完美地对舰船的静磁场进行拟合。

下面给出的是椭球体和偶极子的数学公式。

假设旋转椭球体磁矩为（Mx1，My1，Mz1），则它在测量点（xj，yj，zj）所产生的磁场为

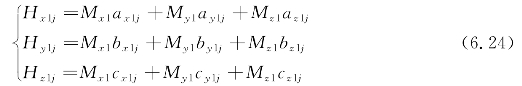
其中，

在磁偶极子列中，设第i个磁偶极子坐标为（xoi，0，0），则它在测量点（xj，yj，zj）所产生的磁场为

其中，

目前，常用的建模方法是椭球体和偶极子混合阵列模型。无论是两种模型中的哪个，从公式来看，当偶极矩位置和大小确定后，其静磁场的大小也就确定了。模型中的椭球体数学公式中含有船长和船宽因子，模拟舰船的整体磁性，偶极子则模拟舰船的局部磁性。

腐蚀相关静电场也会产生腐蚀相关静磁场，但是很难直接测量腐蚀相关磁场。可以利用已经建立的精确计算各种牺牲阳极和ICCP电流组合的腐蚀相关磁场的模型。

6．3．1．3　交变电磁场表征模型

舰船的水下交变电磁场主要来源于螺旋桨及其轴系结构对防腐电流调制产生的轴频电磁场及船体泄漏电流产生的工频电磁场。舰船交变电磁场信号带有明显的基频及谐波特征，例如，螺旋桨对防腐电流调制产生轴频电磁场以螺旋桨转速率为基频，以转速率的倍数为倍频。目前常用于表征舰船水下交变电磁场的数学模型有电偶极子阵列模型与时谐偶极子模型。无论是哪种频率的交变电磁场，由于实际中接收点距离远大于偶极子长度，可以看作是一定频率的时谐偶极子。例如工频看作50 Hz及其谐波的时谐偶极子，轴频可以看作频率与螺旋桨转速相关的时谐偶极子。以轴频电磁场为例，可以将舰船轴频电磁场等效为源强度是Ms=δIL电偶极子，频率为轴频及其谐波（转速／60），δ为调制率，I为流经主轴电流强度，L一般近似为阳极到螺旋桨的水平距离。上述信息获得后就可应用偶极子公式进行数学求解，典型的浅海三层模型电偶极子产生的水下电场数学表达式见第2章有关公式。