MT测深时，由于导电的海水大大抑制了MT信号的高频部分，使得海底以下浅部地层电阻率成像信息缺失，因此MT方法被认为在针对浅部油气（水合物）目标探测中存在盲区。海洋CSEM方法借助大功率人工发射源在近海底建立人工源电磁场，以弥补高频段信号，实现浅部地层的电磁成像。借助海底电磁接收机对含有海底以下地层电性信息的人工场源电磁信号进行高精度采集，经后续资料处理得到海底地层电性信息，用于推断海底以下介质的电性异常，从而评估油气（水合物）储层。相比MT适合深部的低阻异常体探测，CSEM更适合浅部高阻异常体识别。下面从场源特征、异常识别、海上数据采集、资料处理、模型反演五个方面介绍CSEM的原理与工作流程。

1）场源特征与异常识别

从发射源到观测点，海底电磁波共有四种传播路径，如图5.19所示。其中反射波和折射波携带有海底以下介质的电性信息，直达波（包括沿海水和海底沉积层两种途径传播）和空气波是干扰信号。反射波和折射波的幅度在短收发距情况下均小于直达波；在浅海（水深小于300 m）水域较小的收发距条件下反射波和折射波的幅度也小于空气波。因此在浅海水域探测海底目标体应当选取合适的工作参数，以保证得到有效的反射波和折射波信息，从而达到探测高阻异常体的目的。

图5.19　海底电磁波传播路径图

图5.20　水平均匀层状半空间模型图

在海洋水平均匀层状半空间中的水平电偶源电磁场的数值模拟计算中，为了提高计算精度和计算速度，在模拟海底电偶源三维电磁问题时采用Zhdanov等人提出的预条件体积分方程法，实现海底天然气水合物储层的可控源电磁响应模拟。水平均匀层状半空间模型如图5.20所示。对于海洋CSEM方法而言，电偶源一般位于海水层中，也就是模型的第一层中。

采用预条件体积分方程法对海洋轴向水平电偶源激励下的海底均匀半空间和一维天然气水合物储层的电场频率响应进行数值模拟计算，研究观测系统收发距离和侧向偏移、发射偶极源参数、储层几何参数和物性参数等变化对储层异常特征的影响。这为海洋可控源电磁法勘探仪器设计和海上数据采集方案制定提供了理论依据，同时也可以为研究实测资料处理、解释方法奠定基础。

图5.21　含高阻层（天然气水合物储层）的一维模型示意图

图5.21是一维海底天然气水合物储层模型，为四层模型。第一层是海水层，厚度1 000 m，电阻率设为0.33Ω·m；第二层是低阻覆盖层（沉积层），厚度1 000 m，电阻率设为1Ω·m；第三层是高阻天然气水合物储层，厚度100 m，电阻率设为100Ω·m；第四层是向下延伸到无穷远的低阻层，电阻率设为1Ω·m。

若不存在高阻层时，相应的模型为两层模型，即海底均匀半空间或称为背景模型；其可控源电磁响应称为背景响应。

取发射频率为0.5 Hz，数值模拟计算结果如图5.22所示，从图5.22a可以看出，随着收发距增大，两个模型（有异常层模型和背景模型）的电场响应Ex分量幅值都迅速减小。在收发距小于1 000 m或大于17 000 m的范围内，两个模型响应的Ex幅值曲线基本重合。在1 000～17 000 m内，两条曲线明显分开，含储层模型的电场响应Ex分量幅值大于背景模型响应的Ex分量幅值。也就是说，只有收发距保持在1 000～17 000 m时，接收点观测到从海底水合物储层反射的电磁波才能反映异常信息。

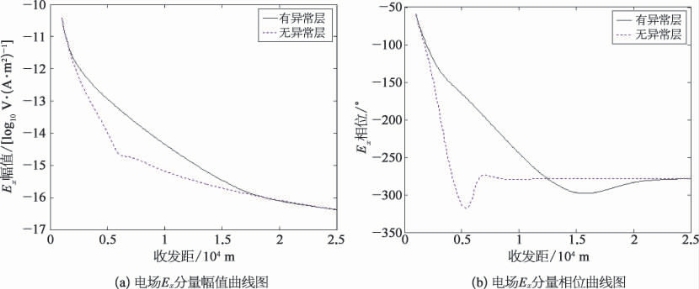
图5.22　海底一维模型响应电场Ex分量幅值和相位与收发距关系曲线图

模型响应的电场分量Ex相位与收发距的关系如图5.22b所示。由图可见，收发距在1 000～21 000 m时，两条相位曲线相差较大，尤其在中间段差异明显。在1 000～12 500 m的收发距范围内，模型响应的Ex分量相位超前背景模型响应的Ex相位；而在12 500～21 000 m的收发距范围内，模型响应的Ex分量相位落后背景模型响应的Ex相位。

由图5.22可知，高阻层在Ex分量的幅值及相位具有异常显示，但是对应的收发距位置不同，引起的异常值也不同，实际勘探工作方案设计过程中，应该根据模型正演计算结果制定最佳观测参数。

用背景模型响应对含异常体模型的响应做归一化处理，可得电场的归一化幅值：

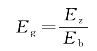
式中　Eg——电场归一化幅值；

Ez——含异常体模型响应的电场幅值；

Eb——背景模型响应的电场幅值。

相位的归一化处理：

式中　φg——归一化幅值；

φz——含异常体模型响应的相位；

φb——背景模型响应的相位。

模型响应的电场分量Ex归一化幅值曲线和归一化相位与收发距关系曲线如图5.23所示。由图5.23a可知，随着收发距的增加，模型响应的电场Ex分量归一化幅值逐渐增大，在6 000 m处取得极大值25；之后随着收发距的增加，归一化幅值逐渐减小，到15 000 m后幅值基本为1。由图5.23b可知，模型响应的电场Ex分量归一化相位曲线形态与幅值曲线形态基本一致，也是随着收发距的增加，归一化相位逐渐增加，在收发距约5 000 m处达到极大值150°，然后开始减小。只是归一化相位曲线在收发距16 000 m处存在极小值。归一化相位极大值对应的收发距小于归一化幅值极大值对应的收发距。

图5.23　海底一维模型响应电场Ex分量归一化幅值和归一化相位与收发距关系曲线图

最佳观测窗口可以根据模型响应归一化幅值曲线和归一化相位曲线选取，窗口中心一般取归一化幅值极大值或归一化相位极大值对应的收发距，窗口宽度应该以包含归一化相位曲线特征点和归一化幅值曲线特征点为准。这样才能观测到最大的海底水合物高阻异常反应。

2）海上数据采集

海洋CSEM海上作业时主要包括作业船及船载大功率甲板电源、船载深拖缆及绞车、船载导航及水下定位设备、大功率拖曳发射机和若干台海底电磁接收机。海洋可控源电磁发射系统用于激励大功率人工电磁场信号。该系统是由船载大功率发电机提供电力，通过甲板变压及监控单元和水下深拖缆，将电力和监控信号输送至海底的电磁发射机，再经过水下变压和整流单元，在发射机主控单元的控制下，通过功率波形逆变单元和发射偶极，把电磁场发射到海底介质中。甲板监测单元可与水下的发射机通信，通过信号电缆完成控制命令和数据交互，查看和更改发射机的运行状态。海底电磁接收机部件分为电子及机械两部分，电子部件包括电场传感器、磁场传感器、采集电路、水声换能器、定位信标、姿态测量装置、甲板单元等；机械部件包括玻璃浮球、框架、测量臂、声学释放器、水泥块、电腐蚀脱钩器及配套的甲板遥控端。其核心功能是实现海底电磁信号的高精度采集。实现这一目标需要解决接收机的高可靠投放与回收、深水耐压、低噪声大动态范围观测、多台接收机与发射机同时工作、导航系统高精度时间同步、水下长时间连续作业、海上高效作业等一系列关键技术问题。

海洋CSEM海上作业示意图如图5.24所示。作业流程主要分为以下步骤：

图5.24　海洋CSEM海上作业示意图(www.daowen.com)

（1）接收机投放。根据目标工作区域测线预设的点位，将海底电磁接收机依次投放至海底。

（2）接收机定位。借助船载USBL水下定位系统对海底接收机位置进行精确定位，并为后期数据处理提供坐标信息。

（3）发射作业与CSEM数据采集。拖曳发射机按照设计的路线及频率进行大功率电流激发，接收机采集CSEM信号与MT信号，此时MT信号为噪声。

（4）MT数据采集。在接收机着底后至回收之前（一般持续1～2周）一直采集海底MT信号。

（5）回收接收机。借助释放回收系统对接收机进行逐点打捞回收。

（6）现场数据预处理。下载接收机中的数据文件，结合发射电流文件、导航及水下定位数据，进行CSEM数据处理与海底MT数据处理，并对数据质量进行现场质量评估。

海上作业结束前，需要提供作业班报、导航数据（作业船舶定位、拖体水下定位、接收机水下定位、方位角）、多台接收机观测的电磁场时间序列、发射电流文件等。

3）资料处理

海洋CSEM资料处理的本质是将接收机数据、发送源数据及导航数据等资料融合，包括时域滤波和合并航行数据，通过这两个步骤可以得到人工源电磁场的幅度随偏移距变化（magnitude versus offset，MVO）和相位随偏移距变化（phase versus offset，PVO）曲线。调整校正的方法来提高原始数据的信噪比，这些方法包括时窗调整分析、极化椭圆分析、场分量旋转、压制空气波、噪声估计及尖峰去噪等。

根据海洋CSEM数据处理的特点，采用模块化处理的思想，如图5.25所示，将基本处理步骤和调整校正方法有机结合起来，可把整个处理流程归纳为四个主要环节：①初始处理；②方位校正；③压制噪声处理；④合并航行数据。其中方位校正处理包括极化椭圆分析和场分量旋转，压制噪声处理包括噪声估计、压制空气波和尖峰去噪。这两个模块里的各种处理方法之间相对独立，处理人员可根据实测资料情况合理选择，并比较不同处理方法的应用效果，得到最佳处理结果。

图5.25　海洋CSEM数据处理程序结构框图

4）模型反演

（1）OCCAM反演算法。

OCCAM算法的目标函数U表示为（Key，2009）

其中右端第一项为模型粗糙度范数，m为M维的模型参数向量，∂为一阶差分算子；第二项为模型参数m与参考模型m*的偏差，P为确定模型参数与其参考值m*粗糙度的权重对角阵；第三项为模型正演响应与数据的拟合项，μ称为拉格朗日乘数，用于平衡模型粗糙度与数据拟合差的作用，W为数据方差权重函数，d为观测的N数据向量，F为模型响应的正演算子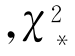为目标拟合差。

求解目标函数U最小值的标准方法是令其一阶导数为0。在对初始模型mk线性化之后，得到如下模型参数更新公式：

其中，d-F（mk）+Jkmk，Jk为线性化的第k次迭代模型响应对电导率对数的一阶偏导数矩阵，称为雅可比矩阵：

反演中，采用均方根（RMS）拟合差公式衡量更新模型的正演响应与数据的拟合情况：

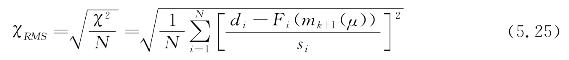
式中　Si——第i个观测数据的误差。

利用OCCAM算法对海洋CSEM数据进行二维反演，能够得到光滑的地电模型并保留模型的主要特征，避免产生过大或过小的模型电阻率参数值及小的虚假构造。

（2）非线性共轭梯度反演算法。

根据Tikhonov和Arsenin提出的理论，采用正则化方法定义非线性共轭梯度的目标函数：

其中正则化参数λ为正数，正定矩阵V-1表示误差向量e的方差，L定义为与三角网格剖分有关的二阶差分算子。通过对关于m的目标函数最小化，得到最佳模型：

式中　Pl——模型空间的搜索方向；

αl——该搜索方向上的最优步长。

搜索方向可通过式（5.29）及式（5.30）迭代求解。式（5.30）中的左端第一项为最速下降方向，第二项用于修正最速下降方向。在线性共轭梯度求解中用于保证当前迭代方向与上一个迭代方向共轭，而在非线性共轭梯度求解中则不做此类要求，只需要共轭搜索方向与梯度满足式（5.31）中给出的弱条件：