
若将深水区看作无限水深,则深海可以等效为空气-海水两层模型,可建立空气-海水两层模型下时谐偶极子水下电磁场数学解析式,通过解析式各组成项分解和物理意义分析,得到一般性的分布规律和传播特性。
空气-海水两层模型如图2.2所示,电偶极子位于海水中,以空气-海水界面作为z=0的平面,z<0的上半空间是空气层,而海水则占据下半空间。空气和海水的电磁参数分别为μ0、ε0、σ0及μ1、ε1、σ1,其中μ0=μ1=μ,σ0=0。
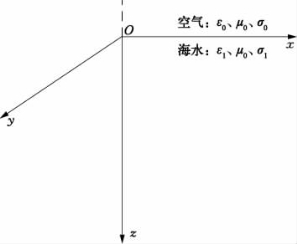
图2.2 空气-海水两层模型示意图
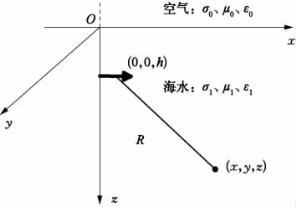
图2.3 两层模型中的x方向时谐水平电偶极子
2.2.1.1 深海环境电偶极子响应
1)x方向水平电偶极子
假定海洋环境为线性、均匀、各向同性媒质。设x Oy平面与空气-海水交界面重合,z轴垂直向下。时谐电偶极子沿x轴正向布于海水中,坐标为(0,0,h),测点坐标为(x,y,z),偶极子电偶矩为P,海水电导率为σ1(图2.3)。假定谐变时间因子为eiωt,其中ω为圆频率。为了满足边界条件,水平电偶极子不仅有与电偶极子同方向的矢量磁位,还有与边界面相垂直的矢量磁位,即An=i Anx+k Anz(n=0,1)。因此对于两层模型,由式(2.3)可得空气和海水中矢量磁位分别满足的约束方程:
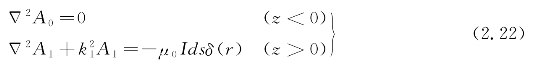
则矢量位An在空气、海水满足如下微分方程:
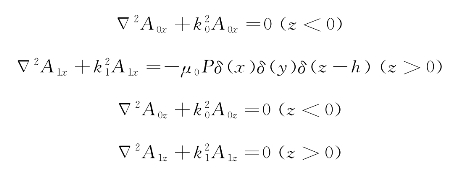
其通解为
其中,![]() =-iμωσ1。
=-iμωσ1。
矢量位的x分量满足边界条件:
矢量位z分量满足边界条件:
联立边界条件求解矢量位约束方程,求解矢量位A:
其中,
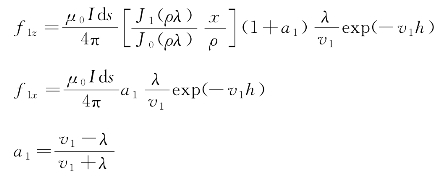
令![]() 然后对矢量位A的表达式进行偏微分,可得海水中磁场三分量表达式:
然后对矢量位A的表达式进行偏微分,可得海水中磁场三分量表达式:
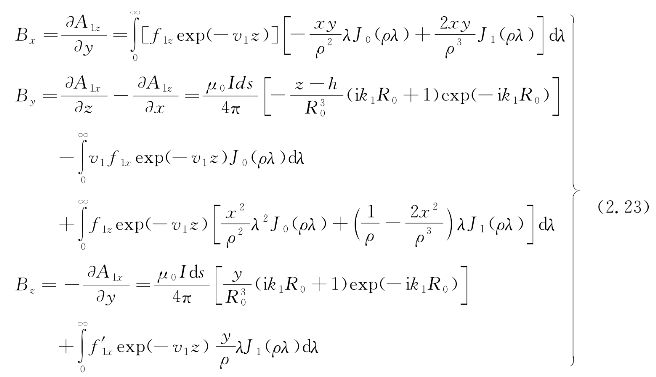
对海水中矢量位A进行偏微分可以得到海水中电场三分量:
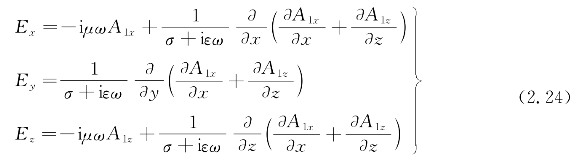
2)y方向水平电偶极子
经过坐标转换,y方向水平直流电偶极子电场响应公式可以用x方向水平直流电偶极子电场响应公式来推导:

式中 x′、y′、z′——x方向直角坐标系正交三分量;
x、y、z——y方向直角坐标系正交三分量,其表示y方向水平直流电偶极子是经过x方向水平直流电偶极子逆时针旋转90°获得。
3)垂直电偶极子
时谐电偶极子沿z轴正向布于海水中,坐标为(0,0,h),测点坐标为(x,y,z),偶极子电偶矩为P,海水电导率为σ1(图2.4)。
从电偶极子第m层(m=0,1)的频率域麦克斯韦方程组出发,引入矢量位Am和标量Um,有
图2.4 空气-海水两层模型示意图
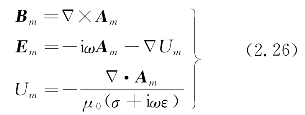
利用罗伦兹条件
![]()
及复波数
![]()
对于z方向电偶极子,Am只有Amz分量,而Amx=0,Amy=0,则矢量位Am在空气、海水和海床层满足如下微分方程:
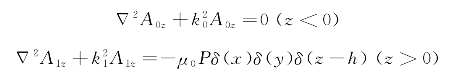
引入相应边界条件:
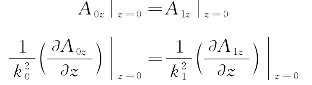
则空气-海水两层模型下,垂直电偶极子在海水中产生的矢量位A1z数学表达式如下所示:
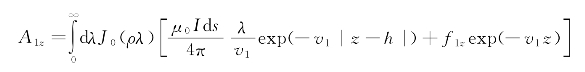
其中,
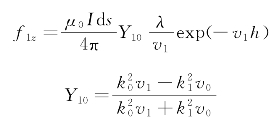
根据式(2.26)中矢量位与磁场的关系,对海水中矢量位A进行偏微分,可以得到海水中磁场三分量:

根据式(2.26)中矢量位与电场的关系,对海水中矢量位A进行偏微分,可以得到海水中电场三分量:
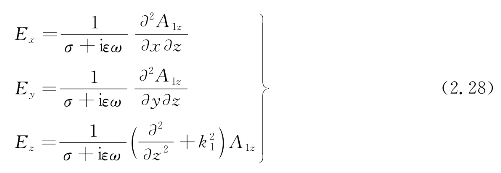
2.2.1.2 深海环境磁偶极子响应
磁性激励源在导电介质中产生涡流电流,其特点是![]() 引入磁性源的矢量位F,即取
引入磁性源的矢量位F,即取
![]()
无源区域频率域麦克斯韦方程为
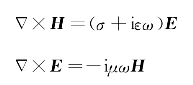
磁性源区域频率域麦克斯韦方程为
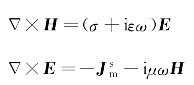
式中 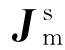 ——磁流密度,
——磁流密度,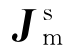 =iμωMs,Ms为源磁流密度,Ms=I Sδ(r)。(www.daowen.com)
=iμωMs,Ms为源磁流密度,Ms=I Sδ(r)。(www.daowen.com)
基于洛伦兹条件,有源区域可以简化为
![]()
其中,k2=-iμω(σ+iεω)。
1)垂直磁偶极子
研究的磁偶极子为垂直磁偶极子,方向指向z轴正向,如图2.5所示。
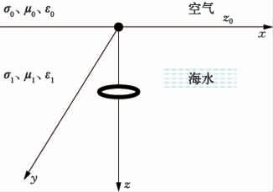
图2.5 两层模型中的交变垂直磁偶极子
设垂直磁偶极子位于海水中点(0,0,h)处,垂直磁偶极子的矢量位只存在垂直分量,由于感应电流都位于水平面内,故电磁场只有Eφ、Hz和Hr分量。因此对于两层模型,由式(2.29)可得空气、海水中矢量位分别满足的约束方程:
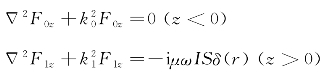
其通解为
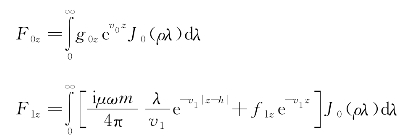
其中,![]() 。
。
满足的边界条件为
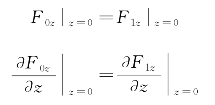
联立边界条件求解矢量位约束方程,可得矢量表达式:
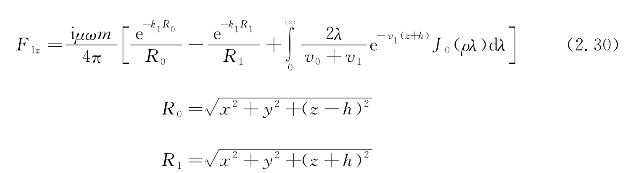
对海水中矢量位式(2.30)进行偏微分,可以得到磁场三分量:
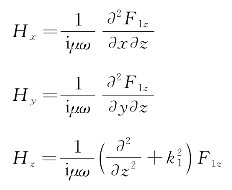
经过简化,得到磁场三分量表达式:

对海水中矢量位式(2.30)进行偏微分,可以得到电场三分量:

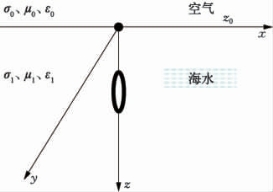
图2.6 两层模型中的交变水平磁偶极子
2)水平磁偶极子
当场源为水平磁偶极子,方向指向x轴正向,如图2.6所示。
设水平磁偶极子位于海水中点(0,0,h)处,水平磁偶极子的矢量位F只有Fx和Fz分量,而Fy=0,即F=i Fx+k Fz。因此对于两层模型,由式(2.29)可得空气、海水中矢量位分别满足的约束方程:
矢量位x分量:
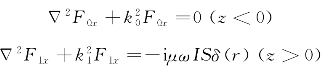
矢量位z分量:
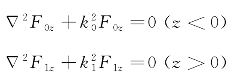
其通解为
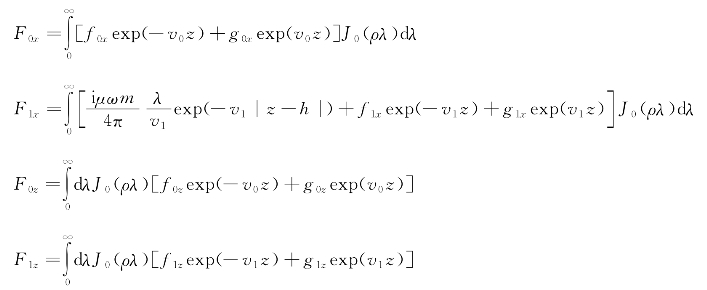
其中,![]() =-iμω(σ1+iε1ω)。
=-iμω(σ1+iε1ω)。
由于Fαx→0,Fαz→0,|z|→∞,α=0,1,则有
![]()
在海面上x分量满足的边界条件为
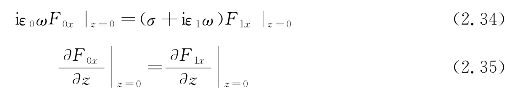
把结果式(2.33)代入通解,再代入边界条件式(2.34)和式(2.35)中,得
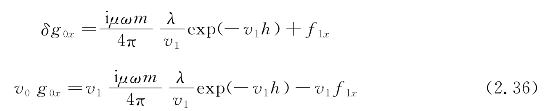
其中,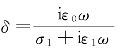 。
。
求解式(2.36)可得
![]()
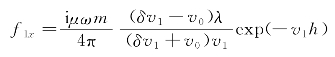
把系数代入通解中,根据索莫菲尔德积分公式可得
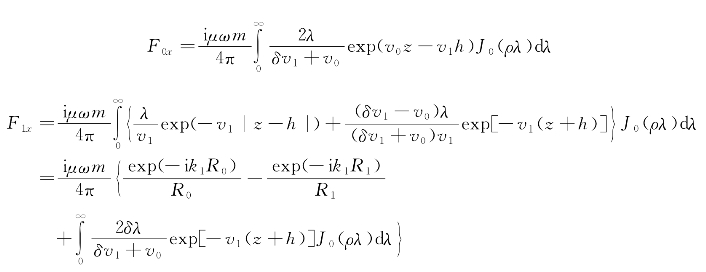
z分量满足的边界条件为
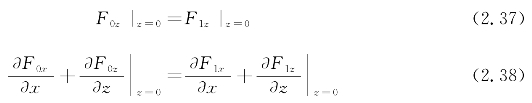
把结果式(2.33)代入通解,再代入边界条件式(2.37)和式(2.38)中,得
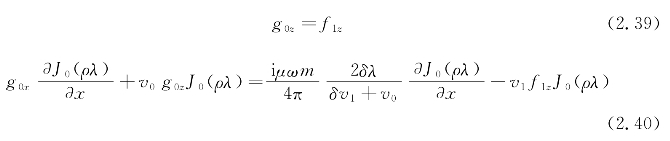
联立式(2.39)和式(2.40),可得
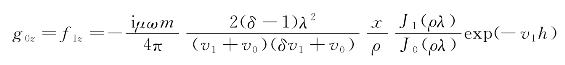
把系数代入通解中,根据索莫菲尔德积分公式:
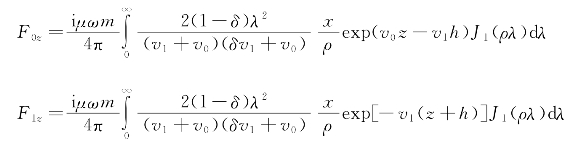
对海水中矢量位F进行偏微分,可以得到磁场三分量:

其中,
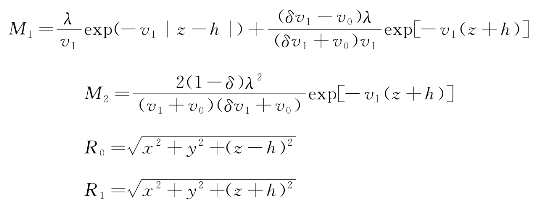
对海水中矢量位F进行偏微分,可以得到电场三分量:
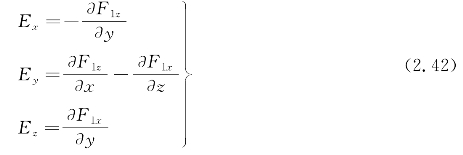
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






