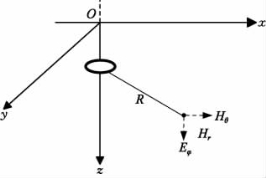
图2.1　磁偶极子坐标示意图

设电流元回路电流I=I ejωt，被电流元回路包围的面积为ΔS，若电流元回路足够小并存在可积边界，可以认为是磁偶极子，表示为变量Mm被称为磁偶极矩。以上即为磁偶极子的完整定义。磁偶极矩的方向是指向面积元ΔS的法线方向，也就是按右手法则环绕这个面积的电流矢量方向。为了方便表述磁偶极子的电磁场，令磁矩的方向沿z轴方向如图2.1所示，同样具备轴对称性（与φ无关），并且它的成分仅仅有一个电分量Eφ和两个磁分量Hr、Hθ。按照在2.1.1节中已经分析的基本方程等基础理论，电场强度分量Eφ满足如下形式：

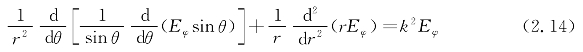
引入函数

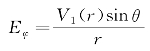
将上式代入式（2.14），可得

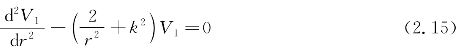
式（2.15）与2.1.1节中所描述的边界条件类似，在k→0时，不存在电场分量Eφ，磁场分量的值Hr可表示为如下形式：

应用第一个边界条件，当k→0时，函数。

当r→∞，有V1（r）→0。

综合上述边界条件，得到

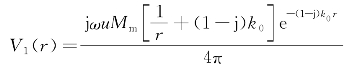
则它的电磁场表达式为(www.daowen.com)

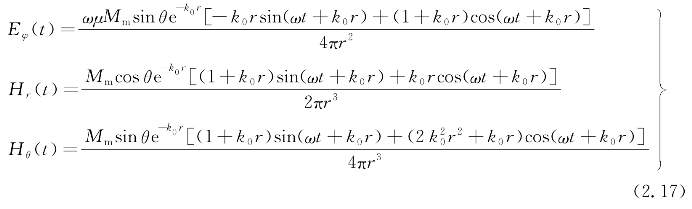
从式（2.17）可以得到除了反映偶极子特性的空间衰减之外，随着相对于源的距离和频率的增加呈指数衰减。在近似的条件下，当k0r＜＜1（介质中的波长λ很小时）可以简化为下式：

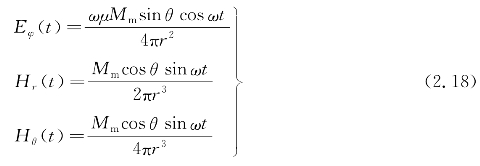
在波数很大的条件下若满足条件k0r＞＞1，可得到下列的近似公式：

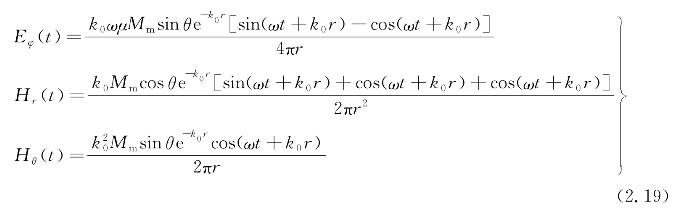
无论是在近场区域还是在满足法拉第感应定律的远场区域，场强分量之间都存在相移。

式（2.17）～式（2.19）分别给出了不同条件下的磁偶极子源的电磁场表达式。

改变对空间和时间的微分顺序，式（2.1）能重写为

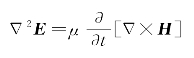
将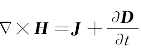代入上式，得到

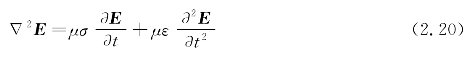
这是导电媒质中电场分量E的表达式。同理也能得出磁场分量H的表达式：

式（2.20）和式（2.21）称为时间域中的一般波动方程，无源均匀导电媒质中电磁场满足一般波动方程。在二阶微分方程中，一阶项的存在表明场通过媒质传播时是存在能量损耗的，因此导电媒质称为有耗媒质。