在第1章简单介绍了偶极子的概念，这里进一步给出电偶极子的完整定义。用导线连接的相互间的距离为无限小Δl的两个电流源系统被称为电偶极子，其中电流I=I ejωt和Δl间的相互关系为的值被称为偶极子矩，它是矢量，单位为A·m。在椭球坐标系中，偶极子所产生的电磁场关于坐标φ轴对称，所以仅有一个磁分量H=Hφ和两个电场分量Er、Eθ。解单分量H=Hφ的标量方程可以确定磁场分量参数，而电场分量参数可以通过对Hφ求微分得到。因为采用的是椭球坐标系（而不是直角坐标系），矢量方程Δ2H+k2 H=0不能直接投影到椭球体坐标系，需要利用旋度把公式展开成如下形式：

假设有Q=r Hφ，代入式（2.6），得到

引入函数关系式Q=V（r）sinθ，容易证明函数V（r）符合第二类微分方程的一般形式，如下所示：

磁场与函数V（r）的关系为

式（2.7）的边界条件为：①当k→0时，电偶极子磁场强度可表示为，那么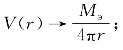②函数V（r）在无限远处有→0。

式（2.7）的解由两部分叠加而成：V（r）=（Ar-1+B）eαr。此处A、B和α为任意常数。把V（r）代入式（2.7），并比较零次自由项和r-1、r-2的因子项，得到几个常数的关系如下：

因为当r→∞的过程中磁场是随着距离减小的，那么α应该带“-”号，α=-k=-（1-j）k0，k0=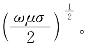这时，

利用边界条件①，很容易确定常数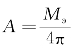的值。这样函数V（r）最终有如下形式：

磁场强度的形式为(www.daowen.com)

直接求解矢量势可以得到

将特征方程写成含有时间参数的形式，令最终得到磁场分量的解：

接下来可以确定Er和Eθ，如下所示：

得到的式（2.8）～式（2.10）表明，电场和磁场的所有分量随着距偶极子距离增加及频率的增加而呈指数性减小。对于Hφ来说，在近距离区域内（或者在低频的情况下），随着距离的变化，衰减速度最小。这样一来，当k0r＜＜1时，

在高频或远距离情况下（k0r＞＞1），可以表示为

式（2.11）和式（2.12）给出了一般情况下电偶极子各分量的计算表达式。电偶极子电磁场分量的相位变化特性有如下特点：在近场所有的分量随着激励电流一起发生同相改变；在远场相位的偏移不只是随着偶极子供电电流发生改变，而且在分量之间也发生相位的偏移。

在小波数的条件下，因为那么就意味着在传导介质中接收点相对源的距离远小于波长。在这个距离上场的空间变化不取决于频率，它通常被认为是稳恒场。因此在直角坐标系和稳恒条件下电偶极子电磁场的强度表示成如下形式：

式（2.11）～式（2.13）分别给出了不同条件下电偶极子源的电磁场表达式。