对于全轮驱动汽车，往往由于轮胎气压选择不当，致使各车轴轮胎变形不等，车轮滚动半径和行驶路径不等，这就造成了功率循环和功率损失，加速轮胎和相关零部件的磨损。为避免或减轻这一现象，应按如下措施选取轮胎气压。

1.对于二轴全轮驱动汽车

二轴汽车，无论是货车、乘用车，还是特种车，前、后轴的负荷往往差别很大。同一种轮胎，负荷不同，需要选取不同的气压来保证轮胎的变形基本一致。

对于4×2的汽车来说，前后轮胎的变形是允许有一定差值的，然而对于4×4的全轮驱动汽车来说则是绝对不允许的，必须按下述方法选定轮胎气压。

首先可用式（4-61）选定二轴中任一轴的气压，然后利用式（4-56）计算该轮胎的变形f_t，最后利用下式计算另一车轴的轮胎气压p_w：

式中；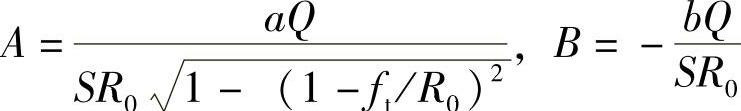

Q——另一车轴的单轮负荷（N）；

S——轮胎断面宽（cm）；

R₀——轮胎半径（cm）；

f_t——已定胎压车轴轮胎的变形（cm）；

a、b——系数，a=22.54，b=-21.54。

式（4-62）是一个隐函数，在算出A、B数值后，可进行迭代处理。由该式确定的

轮胎气压p_w，再代入式（4-56）计算的轮胎变形，即为f_t。

2.对于三轴以上的全轮驱动汽车

二轴全轮驱动汽车，可通过调整前、后轴轮胎的气压来避免功率循环，然而，对于三轴以上的多轴汽车则是十分麻烦的。例如，一辆8轴汽车就有8种气压，那是不可想象的！(www.daowen.com)

对此，在进行汽车设计时，可通过各轴等轴负荷分配来解决这个问题。因为同样的轮胎，同样的负荷，加上同样的气压，就可获得同样的轮胎变形。

多轴汽车各轴等负荷分配，是可以通过车体绕簧外瞬心振动的假设建模来实现的。

要实现各轴等轴负荷分配，各轴悬架的刚度c_i必须按下式取值：

式中 G——车辆总负荷（N）；

l——整车质心面至第1轴的距离（cm）；

n——车轴数；

f₁——第1轴悬架的静挠度（cm）；

f——整车质心面的静挠度（cm）；

l_i——各轴至第1轴的距离（cm）。

f₁和f是设计时，对第1轴和质心面处的频率N₁和N的要求来决定的。

注意：若N₁＞N，则f₁＜f。此时外心在左侧，反之在右侧。

各轴轴距l_i的确定必须满足式（4-66）的要求，否则不能实现各轴等负荷分配。

有了式（4-63）的刚度值，就可以利用式（4-67）计算均布轴荷G_i，为

这个轴荷能满足G_i=G/n。若设n_g为轮胎总数，那么，车轮负荷Q_i=G/n_g。有了Q_i，再选定了轮胎，主参数系数M_e就确定了。至此，就可用统计方程式（4-61）计算选定公路行驶气压p_w了。