线性悬架行程和容量的分配,可参照图4-5进行。
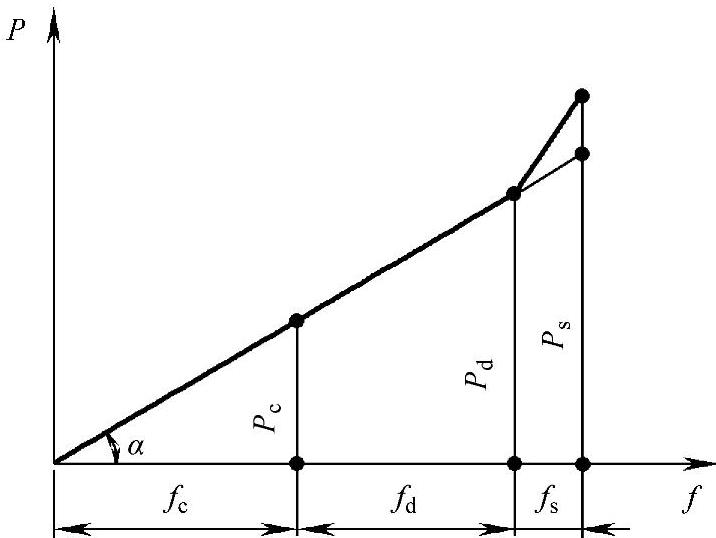
图4-5 线性特性悬架的匹配
fc—静挠度(cm) fd—动挠度(cm) fs—限位行程(cm) Pc—满载负荷(N) Pd—动行程最大时的负荷(N) Ps—限位块“铁碰铁”时的负荷(N)
1.给定静挠度fc
当悬架频率n的单位取为次/min时,静挠度可表示为
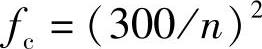
注意:假若悬架的刚度为c=tanα(N/cm),那么fc值必须满足等式Pc=cfc。若fc不能满足此式,则必须调整所给刚度特性。
2.计算静容量Uc
静容量表示为
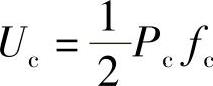
3.计算动挠度fd
按以上的结论,为获得最大动容量,应取fd=fc。当受到车辆结构限制时,fd值也可以适当下调,但最小不能小于0.8fc。
4.计算复原行程fr
动挠度fd是压缩行程,fr是其复原(反弹)行程,根据能量吸收情况,由于半周期振幅比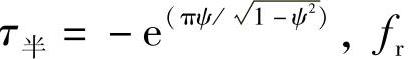 应由下式计算:
应由下式计算:

式中 ψ——阻尼比,一般ψ=0.25~0.35;
Δ——富余量,一般取Δ=15mm。
5.计算动容量Ud
由于取fd=fc,由图4-5的几何关系,有

如果取fd=0.8fc,那么Ud=2.4Uc。(https://www.daowen.com)
6.计算动行程终点的载荷Pd
动行程终点的载荷Pd,也是悬架将要碰触而又未碰触缓冲块时的载荷,按图4-5的几何关系,有
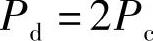
注意:Pd=2Pc在相应变形下还不一定落在所选刚度特性曲线上。如偏离太远,还需调整所给刚度特性或调整Ud值。此外,还可用下式来进行检验:

式中 Ps——限位载荷,也是弹性元件材料的允许极限负荷。
如果Pd远不能满足式(4-40),则同样需要调整刚度特性或Ud值。
7.计算限位载荷Ps
限位载荷Ps是悬架与限位块“铁碰铁”时的载荷,它接近悬架弹性元件材料的允许极限负荷。对于螺旋弹簧来说,也近似等于“压并载荷”。在此载荷下,汽车油底壳等脆弱部件还不致受到触碰。建议限位载荷按下式取值:

注意:限位载荷不能大于弹性元件材料的允许极限载荷。
8.确定限位行程fs
假设限位块的刚度为cs,那么,当悬架限位块接触后,悬架的刚度就变成了0.25Pd/fs=c+cs,于是有

为降低成本,若无十分必要,限位块的刚度不宜制成非线性的。
9.确定限位容量Us
由图4-5的几何关系可得:
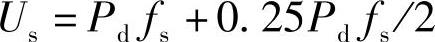
解之可得
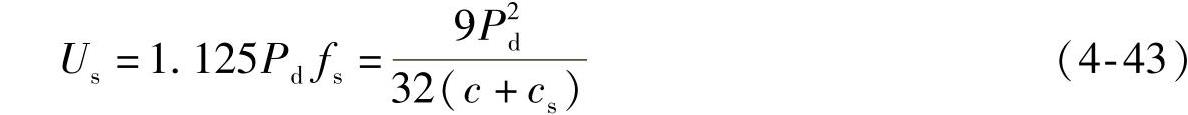
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






