所谓均布轴负荷，就是汽车整车总负荷P均匀分布于各车轴n的载荷P/n。载荷均布有着如下优点：

①能提高通过性。在汽车总载荷已定的情况下，载荷均布的实质就是避免某一车轴负荷过高，从而减小在软地面上的下陷和提高越障能力等。

②能保护路面和提高桥梁等设施的安全。

③能相对降低相关零部件的载荷，提高可靠性。

④能使各车轴轮胎的气压和变形相等，保持车身状态避免驱动车轴的功率循环等。

1.计算公式的建立

如何才能实现均布轴负荷呢？这与各轴轴距l_i和各轴刚度c_i等因素有关。下面分别叙述。

（1）选定各轴轴距l_i

在整车负荷P、质心位置l和车轴数n已定的情况下，根据图4-1的关系，各轴轴距l_i必须保证力矩平衡，即应使。因为各轴负荷P_i=P/n，所以必须使：

若不能满足式（4-23）的条件，就不可能实现均布轴荷。式（4-23）对于n≥3的汽车，既有理论意义，也有实际意义。然而，对于n=2的汽车，特别是二轴货车，因为重心偏后，总轴距又不能随意改动，故虽有理论意义，但事实上却是难以实现的。

（2）选定各轴的刚度c_i

此处各轴的刚度c_i应是弹簧刚度c_s和轮胎刚度c_t的串联组合刚度，即

各轴的刚度c_i应是由式（4-24）所决定的刚度，它取决于各轴的变形f_i，即

式（4-25）中的f_i可以根据整车质心面处的变形f和第1轴处的变形f₁的设计要求来决定。假定要求质心面处的频率为N（注意：此频率略低于悬架频率，因增加了非悬挂质量），并要求第1轴处的频率为N₁，那么，质心和第1轴处的变形分别为

注意：若N₁＞N₂，则f₁＜f，此时外心在左侧，反之则在右侧。

在上述假设下，车体的满载角位移为

各轴的变形为

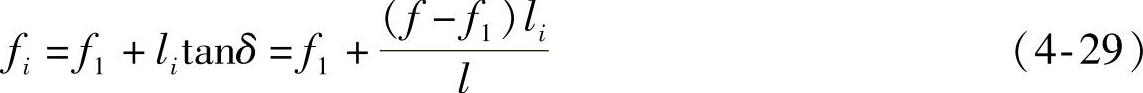
将式（4-29）代入式（4-25），便可得到各轴的刚度：

若N=N₁，f=f₁，δ=0，即外心距在无穷远处，此时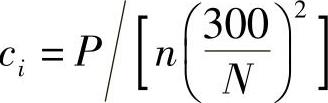，。(www.daowen.com)

有了式（4-30），就能计算均布轴荷了：

2.计算示例

某8轴汽车，即n=8，整车总负荷P=1196000N，质心面至第1轴的距离l=740cm，各轴至第1轴的距离：l₁=0，l₂=205cm，l₃=430cm，l₄=635cm，l₅=840cm，l₆=1065cm，l₇=1270cm，l₈=1475cm。设计要求质心面处的频率N=90次/min，第1轴处的频率N₁=95次/min（注意：此频率比悬架频率略低，因增加了非悬挂质体载荷）。求各轴悬架的刚度c_i。

具体计算：

①用式（4-23）检验力矩是否平衡：

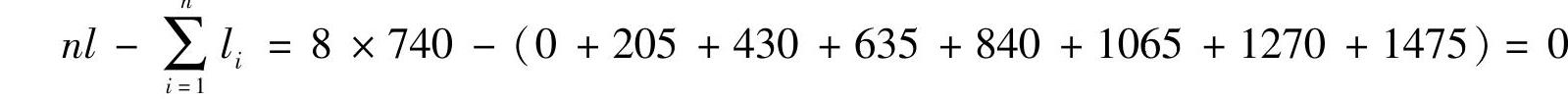
力矩已达平衡，轴距不需调整就可实现均布轴荷。

②用式（4-26）计算质心面处的静挠度：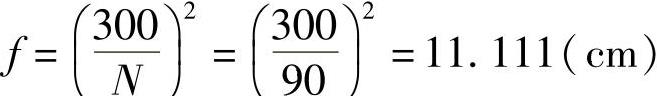

③用式（4-27）计算第1轴处的静挠度：

④用式（4-28）计算车体角位移：

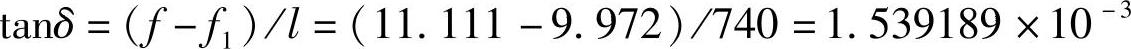
⑤用式（4-29）计算各轴处的静挠度，计算结果如下：

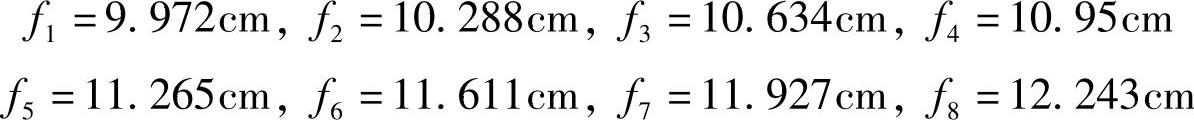
⑥用式（4-25）计算各轴处的刚度，计算结果如下：

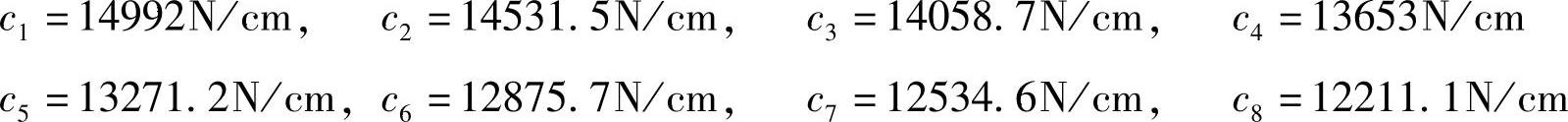
⑦用式（4-31）计算各轴的负荷，计算结果如下：

由计算结果可知，P_i值与P/n=149500N值误差极微。

⑧用式（4-19）计算刚度分配比：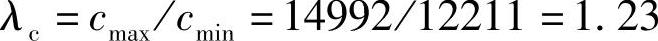

⑨用式（4-14）计算频率分配比：

上述三种负荷分配法各有其优点，也各有其用途，到底如何选取，须根据车辆的用途、使用环境以及公司的生产条件等来决定。常驶于一般路面的汽车，可以考虑降低成本，采用等刚度设计；常驶于坏路面的汽车，则应考虑运输安全性和机动性，采用等频率和均布轴荷分配法。然而，这也并非是绝对的，重要的是要综合权衡，心中有数。例如，本书等刚度负荷分配法一节所举的例子（n=6），不仅各轴弹簧刚度相等，便于设计生产、降低成本，而且负荷分配比只有1.06（当然，这个负荷不包括非悬挂质量），频率分配比只有1.03，像这样的分配方案就是可取的。

值得注意的是，均布载荷法所举的例子，其刚度分配比λ_c和频率分配比λ_N均较高，但这可通过降低N₁值来调小。若使N₁=N，还可实现等负荷、等刚度和等频率的统一。