所谓等频率负荷，就是保证各车轴悬架频率相等时的悬架载荷，它是悬挂质体载荷在各轴悬架上的分配。当各轴悬架频率相等时，可提高乘坐舒适性和货物及运载设备（如导弹等）的安全性（没有角位移），故提出了等频负荷这一设想。

1.计算公式的建立

求取等频负荷，就是要在已知悬挂质体载荷P，质心在第1轴的距离l和各轴位置l_i以及所希望的各轴频率N的情况下，确定各轴悬架的刚度c_i。

根据设计要求的频率N，可得各悬架弹簧的变形量为

式中 f_i——各悬架的变形（cm）；

N——各悬架的频率（次/min）。

由于各悬架的变形和频率都相等，外心距R₀→∞，质心面与中性面重合，故质心面处的刚度c等于中性面处的刚度c₀，假设汽车的总轴数为n，则有

由式（4-15）和式（4-16）可得

由转矩平衡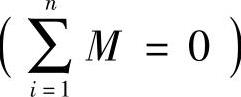）的关系，加之变形f_i为常数，可得

如何把式（4-16）的刚度分配于各个悬架呢？这只需要做到下述两点：

①满足式（4-15）～式（4-18）的条件。

②使分配所得的刚度分配比λ_c为最小。

刚度分配比λ_c就是刚度分配所得的最大值c_max与最小值c_min之比，即

使λ_c值最小的目的，在于使各轴的等频负荷P_i分布较为均匀。λ_c值一般不超过1008。

假设质心面左侧各轴悬架刚度均为c_f，右侧各轴悬架的刚度均为c_r。并设质心面在第K轴和第K+1轴之间（若质心面正好落在某一轴线上，则把此轴叫做第K轴），那么右侧各轴悬架的刚度为

利用式（4-18）的关系可得(www.daowen.com)

将式（4-20）代入式（4-21），可解得左侧各轴悬架的刚度。

能够满足等频分配的刚度c_i和载荷P_i，从理论上说有无穷组，但唯有由式（4-20）和式（4-22）所决定的等频刚度而推出的等频载荷才能保证载荷分布最为均匀。值得注意的是，负荷分配比λ_P是随轴数n的增大而减小的。当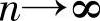时，λ_P=1。

2.计算示例

某4轴汽车，即n=4，悬挂质体负荷P=351800N，质心面至第1轴的距离l=380cm（k=2），各轴至第1轴的距离：l₁=0，l₂=220cm，l₃=550cm，l₄=770cm。设计要求各轴悬架频率N=100次/min，求取各轴理想载荷P_i。

具体计算：

①用式（4-15）计算各轴静挠度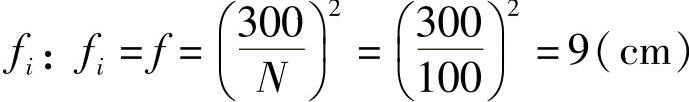

②用式（4-16）计算质心面处的组合线刚度c₀：

③用式（4-22）计算左侧各悬架刚度c_f：

④用式（4-20）计算右侧各悬架的刚度c_r：

⑤用式P_i=c×f_i计算各轴悬架的等频负荷：

⑥用式∑P_i验算各轴负荷和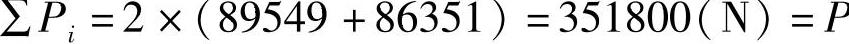：（计算精确）

⑦用式（4-9）计算负荷分配比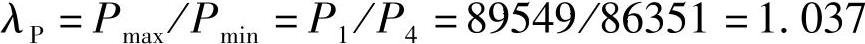：（分配均匀）

⑧用式（4-19）计算刚度分配比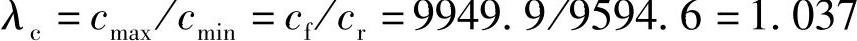：（分配均匀）

⑨用式（4-10）检验频率分配比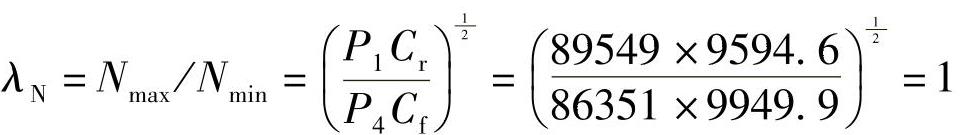：（分配准确）