所谓等刚度负荷，就是各轴悬架刚度相等时各轴悬架的载荷或各轴的轴负荷。虽为同一组刚度，但由悬挂质体载荷决定的为各轴悬架载荷，而由整车总负荷决定的则为各轴的轴载荷。

各轴悬架刚度相等，其优点是各轴悬架结构可以通用，简化设计制造，降低成本，方便维修。下面建立计算公式并举例计算。

1.计算公式的建立

等刚度的数值，从理论上说有无穷多组，但到底取什么样的数值才算合理呢？这和设计要求有关。假设要求悬挂质体（整车）质心面处的频率为N，那么便可导出各轴悬架的刚度值c_e了。

根据所要求的频率N，便可求出悬挂质体（整车）质心面处的变形量为

式中 N——设计要求的悬挂质体（整车）质心面处的频率（次/min）。

由式（4-11），可得质心面处的刚度为

根据式（4-7）的关系，可以导出所要求的各轴的等刚度c_e的计算公式：

式中 n——多轴汽车的轴数；

l——质心到第1轴的距离（cm）；

l_i——各轴到第1轴的距离（cm）。

由式（4-8）可知，等刚度载荷P_i为

式中，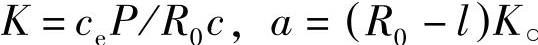

为考察负荷分配的均匀性，还需要用式（4-9）和式（4-10）检验负荷分配比λ_P和频率分配比λ_N。

2.计算示例

某6轴汽车（n=6），悬挂质体负荷P=600600N，悬挂质体质心面至第1轴的距离l=700cm，各轴至第1轴的距离：l₁=0cm，l₂=220cm，l₃=680cm，l₄=900cm，l₅=1120cm，l₆=1340cm。设计要求：质心面处的频率N=95次/min。求各轴悬架的等刚度（均布刚度）c_e和各悬架负荷P_i。(www.daowen.com)

具体计算：

①用式（4-11）计算质心面处的变形量为

②用式（4-12）计算质心面处的刚度为

③用式（4-13）计算各轴悬架的等刚度：

式（4-13）中的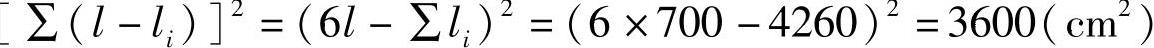

式（4-13）中的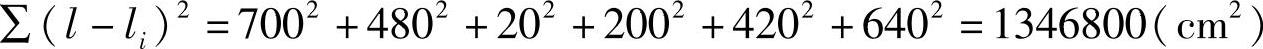

④用式（4-4）计算振动中心距为

负值说明振动中心距在右侧。

⑤用式（4-14）计算各轴等刚度负荷。

式（4-14）中的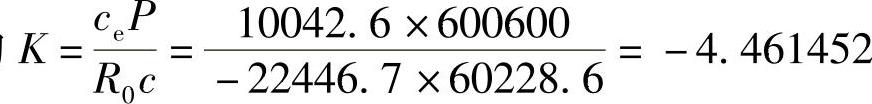

式（4-14）中的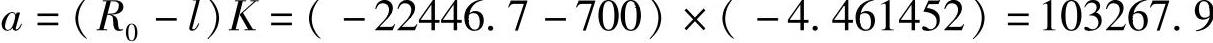

⑥用式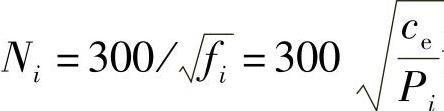计算各轴悬架的频率，计算结果：

N₁=93.6次/min，N₂=94次/min，N₃=95次/min，N₄=95.4次/min，N₅=95.9次/min，N₆=96.4次/min

⑦用式（4-9）计算负荷分配比：λ_P=P₁/P₆=103263.4/97289.6=1.06。此值说明各轴悬架负荷分配较为均匀。

⑧用式（4-10）计算频率分配比：λ_N=N₆/N₁=96.4/93.6=1.03。此值说明各悬架频率分配相当好！