在已知整车负荷（悬挂质体负荷）P、整车质心（悬挂质体质心）至第1轴的距离l、各轴至第1轴的距离l_i以及各轴悬架刚度c_i的情况下，利用图4-1的力学模型，来建立各轴轴荷（悬架负荷）P_i的检验计算公式。检验计算其实也是设计计算的一种手段，是为设计计算服务的。

图4-1 质体绕外心倾斜振动

图4-1是一个与多轴汽车对应的多簧质量系统的力学模型，它由刚度为c_i（双边弹簧刚度c_s与双边轮胎刚度c_t的串联组合刚度）的几个弹簧并联组成。各簧（轴）至第1弹簧（轴）的距离为l_i。系统为一刚性质体，其质心面至第1弹簧（轴）的距离为l。

假定在系统的质心面处作用一个垂直载荷P，质体将绕振动中心O转过一个δ角，且各簧将产生一个垂直变形f_i，质心面处的垂直位移为f。

设各轴的负荷（弹簧的变形力）为P_i，而P_i=c_if_i，因c_i为已知参数，故只要求出了f_i，负荷分配问题就解决了。

由图4-1的力矩平衡关系可得

由图4-1的几何关系还可得

将式（4-2）变为

式中 R₀——振动中心到质心面的距离。

将式（4-3）代入式（4-1）后，便可求得振动中心距R₀为

如果式（4-4）中的分母为零，则R₀→∞，瞬心在无穷远处，这意味着质心面与中性面重合，质体产生平上平下的运动。

式（4-3）中的f还是一个未知数，由于f=P/C，P是已知参数，而c是质心面处的换算刚度，它可由下述方法求得：

在图4-1中，由力平衡关系可得

(www.daowen.com)

将式（4-3）代入式（4-5）后，可得

再将式（4-4）代入式（4-6）还可解得

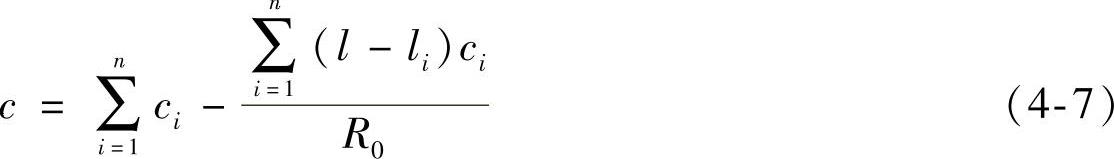
由式（4-7）可知，质心面处的换算刚度（系统组合线刚度），一般小于各簧刚度之和。

有了振动中心距R₀和质心面处的换算刚度c，就可得到各轴的负荷P_i为

值得注意的是，若视P为整车负荷，l为整车质心位置，则P_i为各轴的轴荷；若视P为悬挂质体载荷，l为悬挂质体质心位置，则P_i为各轴悬架负荷。

式（4-8）适用于n轴汽车，故也适用于二轴汽车。

由式（4-8）可知，各轴负荷P_i除与总负荷成正比外，还与相对刚度c_i/c和相对轴距（l-l_i）/R₀有关。

为考察负荷分配的合理性，需要用负荷分配比λ_P和频率分配比λ_N来检验：

式中 P_max、P_min——各轴负荷的最大值和最小值。

式中 N_max、Nmin——各轴频率的最大值和最小值。

f_max、f_min——各轴弹簧变形量的最大值和最小值。

λ_P和λ_N的数值不可过大，其理想值为1。