1.阻尼系数表达式

减振器的阻尼系数是阻力-速度特性曲线的斜率，即K=dP/dv。在悬架刚度c和悬挂质量m以及阻尼比ψ均已给定的情况下，阻尼系数K为

式中 ψ_簧——弹性元件的当量相对阻尼系数。

δ——减振器轴线J_dJ_u与CJ_d线的垂线之间的夹角，点C是减振器下支点J_d的运动瞬心（悬架中心），如图3-136所示。

当量相对阻尼系数可计算为

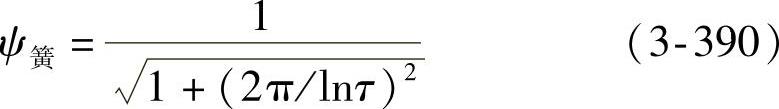
式中 τ——相邻周期振幅比，即τ=A_i/A_i+1，它可由去掉

减振器的试验曲线测出。在设计新车之前，

可根据板簧的片数和长度酌情取值。

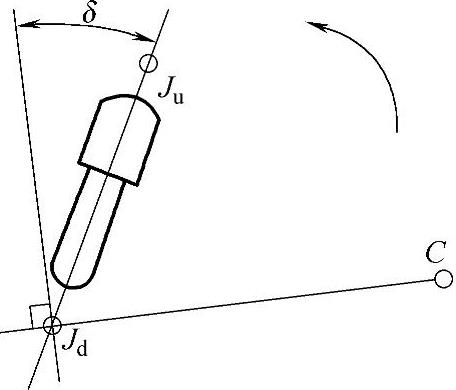
图3-136 减振器的布置角度

利用式（3-389），在设计时便可确定减振器的阻尼系数了。然而，一旦减振器制作出来之后，又如何按示功图来确定和检验它的阻尼系数呢？

2.按示功图确定阻尼系数

利用示功图确定减振器阻尼系数的方法有很多，同一个示功图，采用不同的方法处理，得出的阻尼系数值却相差很大，因此有必要来研究一下这个问题。

下面介绍常用的三种方法：特定值法、P-v图法和平均值法。

在分析研究之前，先简单介绍一下汽车减振器试验台和示功图的有关情况。

减振器性能试验台的工作原理如图3-137所示。试验台的规范：转速n=100r/min，滑块A的行程S₀取为100mm。S₀是曲柄长度R的2倍，且是减振器活塞的实际行程。减振器缸筒下端B和扭杆弹簧O₂B相连，故活塞与缸筒的相对行程S小于S₀。记录板随滑块上、下平移，画针O₂a由弹簧杆牵动。

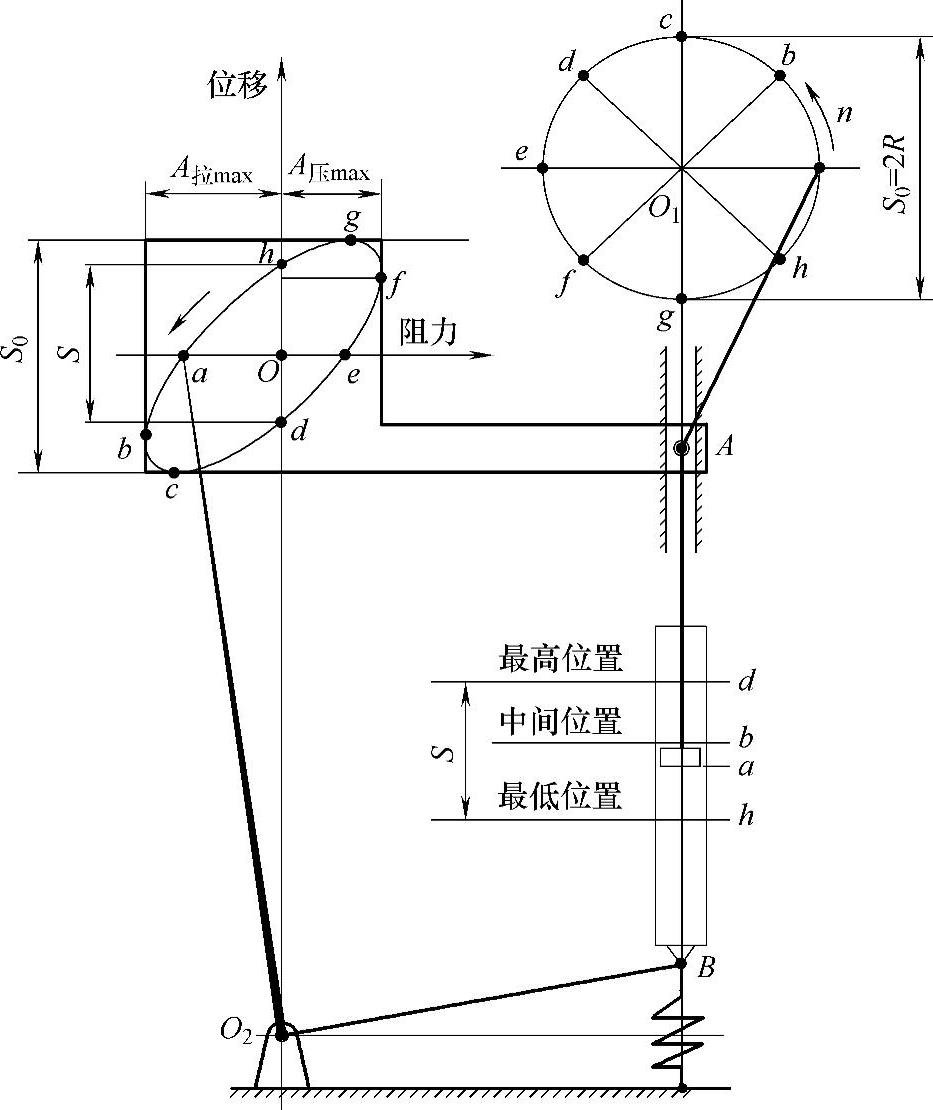
图3-137 减振器性能试验台的工作原理

“双百规范”试验台的活塞速度v=0.52m/s，这个速度需要提高。目前我国个别公司的减振器v值已近1m/s，国外已有大于2.5m/s不畸变的减振器。

当曲柄机构运动时，画针端点a在记录板上留下的迹线便是示功图。它的横坐标代表阻力，纵坐标代表位移，面积代表功。每个试验台都有各自的校正系数α_校。而且压缩行程的校正系数α_压校和复原行程的校正系数α_拉校在数值上还不一定相等。α_校和横坐标数值A之积才是减振器的阻力P。最大压缩阻尼力为

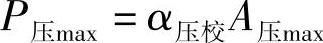
最大复原阻尼力为

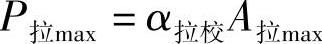
α_校和示功图的面积F之积是减振器所做的功W。压缩行程的面积（S_defghd）F_压与α_压校之积代表压缩行程所做的功W_压，即W_压=α_压校F_压。复原行程的面积（S_habcdh）F_拉与α_拉校之积代表复原行程所做的功W_拉，即

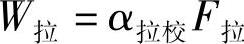
大家知道，在工作范围内，一般认为阻尼力为

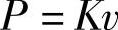
式中 v——活塞的相对速度。

阻尼系数K又分为压阻系数K_压和拉阻系数K_拉，而总的周期阻尼系数为

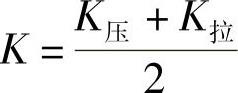
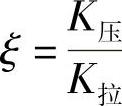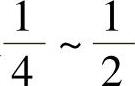为减少传递到车身上的冲击，保证车轮与地面的良好附着，压阻系数和拉阻系数的比值一般取。为减少制动时车身的角加速度，前桥的压拉阻尼系数比应大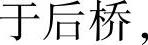即ξ₁>ξ₂。

下面首先介绍三种按示功图确定阻尼系数的方法，然后分析比较每种方法的优劣。

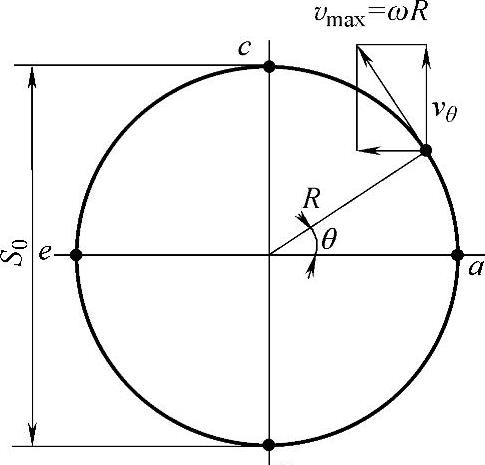
图3-138 v_m与v_θ的关系

（1）三种方法的公式推导

1）特定值法。

在曲柄连杆机构式的减振器试验台上，活塞的运动速度是和曲柄端点在垂直方向上的运动速度v_θ相关的，参见图3-137和图3-138。

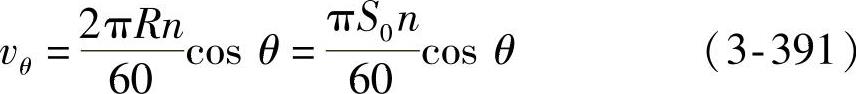
当曲柄端点在a、e位置时，v_θ达到最大值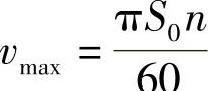，而此时在示功图上，横坐标也相应出现最大值A_max，即阻力也出现最大值P_max=α_校A_max。所谓特定值法，就是抓住这种特定点，来推求阻尼系数K_特，即

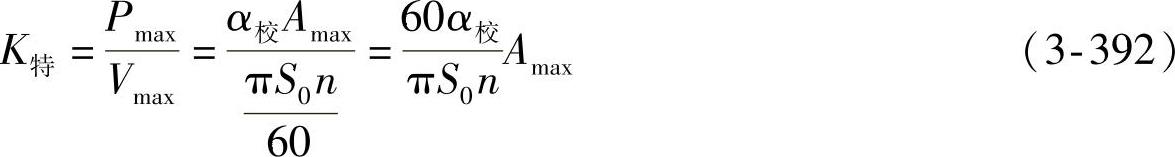
当前，不少人就是按此方法利用示功图来确定阻尼系数的。然而，在试验台中，减振器的下支点是被连接到一个扭杆弹簧的臂上，因此，活塞的实际行程S₀就要大于活塞相对于缸筒的行程S，故活塞相对于缸筒的运动速度可近似表示为

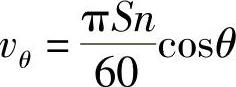
由此，阻尼系数应取值为

活塞相对速度的这种近似计算方法是否可靠呢？严格的方法，应该是从理论上找出活塞相对速度与减振器及试验台相关参数的关系，然后再推求阻尼系数为

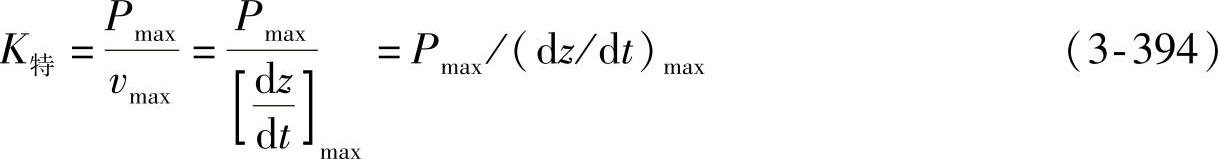
先利用图3-139的关系导出v_θ=f（θ）的关系式。在图3-139中，曲柄长度R=S₀/2，连杆长度为l，θ是曲柄的任意转角，C是连杆端点A、P的运动瞬心，ω是曲柄的角速度。

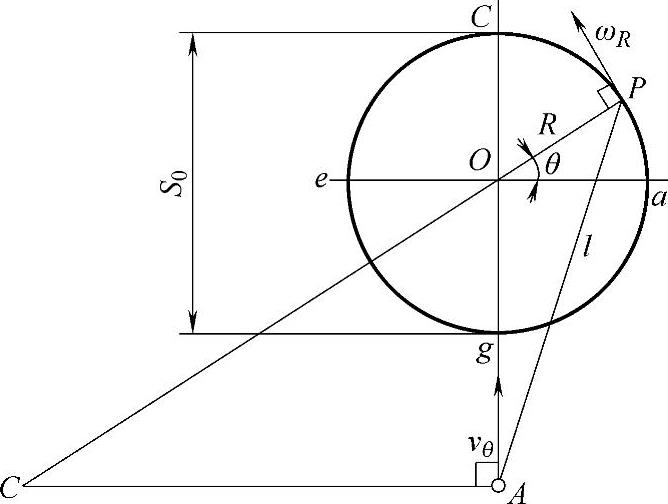
图3-139 v_θ的推求

曲柄端点的线速度ωR与连杆下端点A在垂直方向上的运动速度v_θ的关系为

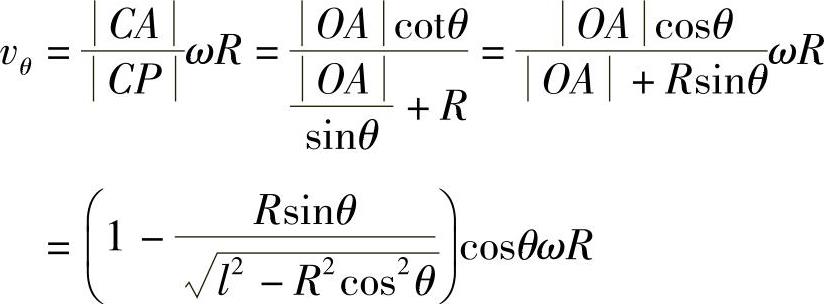
因为

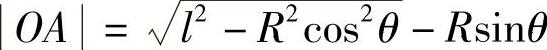
所以有

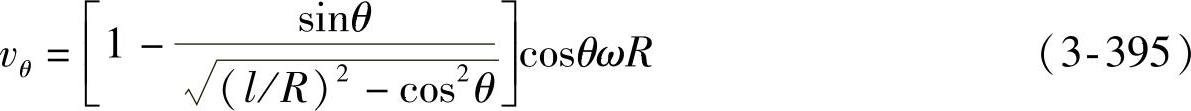
再来推求活塞与缸筒的相对位移Z与曲柄转角θ的关系。如图3-140所示，Z是滑块位移Z₁与缸筒（下支点）位移Z₂的差，即

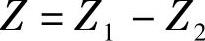
而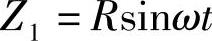

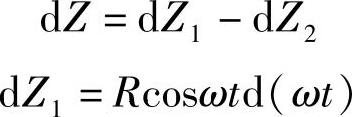
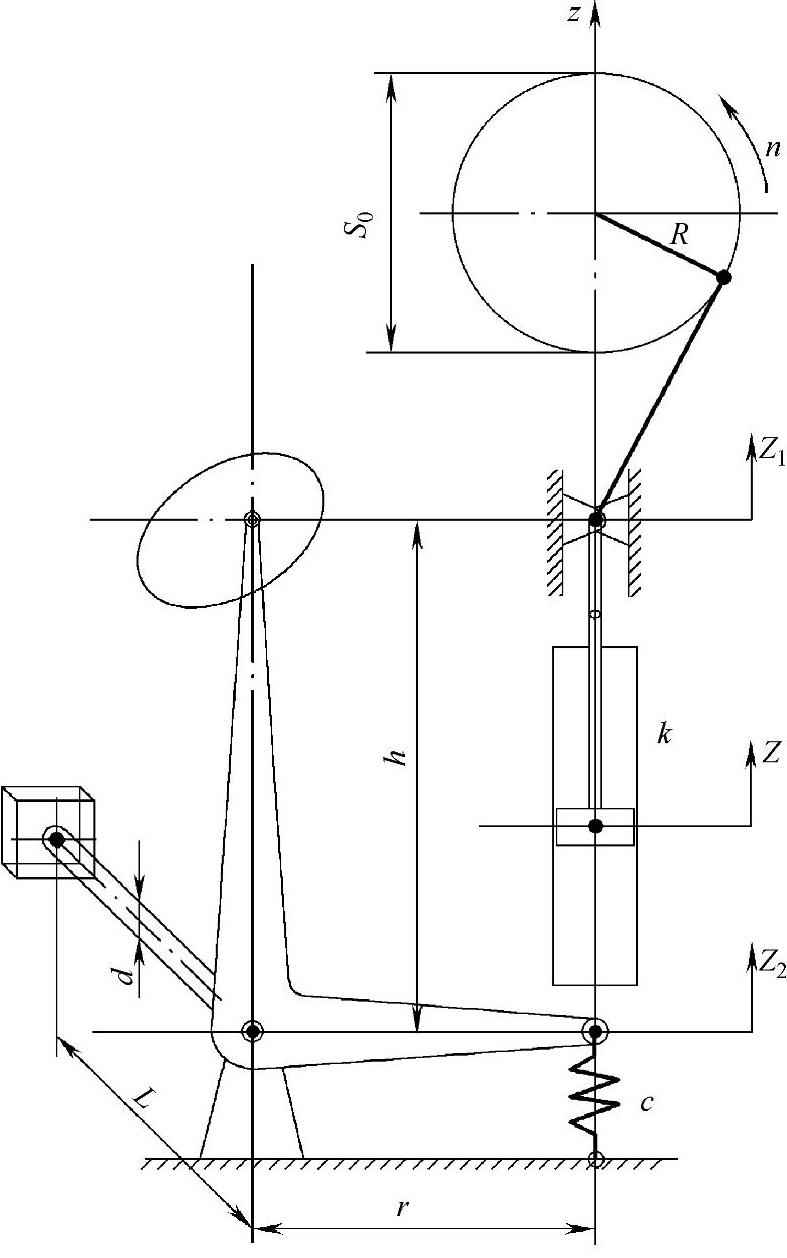
图3-140 Z与θ的关系

对于dZ₂这一项，必须先找出Z₂=f（ωt）这个函数关系式，才能求得。

若假设阻尼力是速度的线性函数，且不计加速阻力，那么由缸筒的力平衡关系，可得方程为

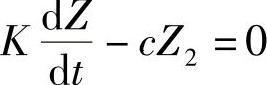
式中 c——扭杆的换算线刚度。

再将dZ=Rcosωtd（ωt）-dZ₂代入上式，便得到

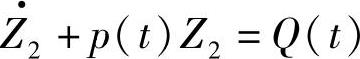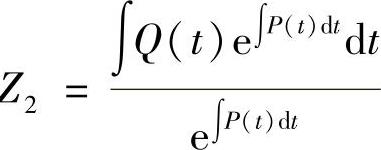根据和，可求得

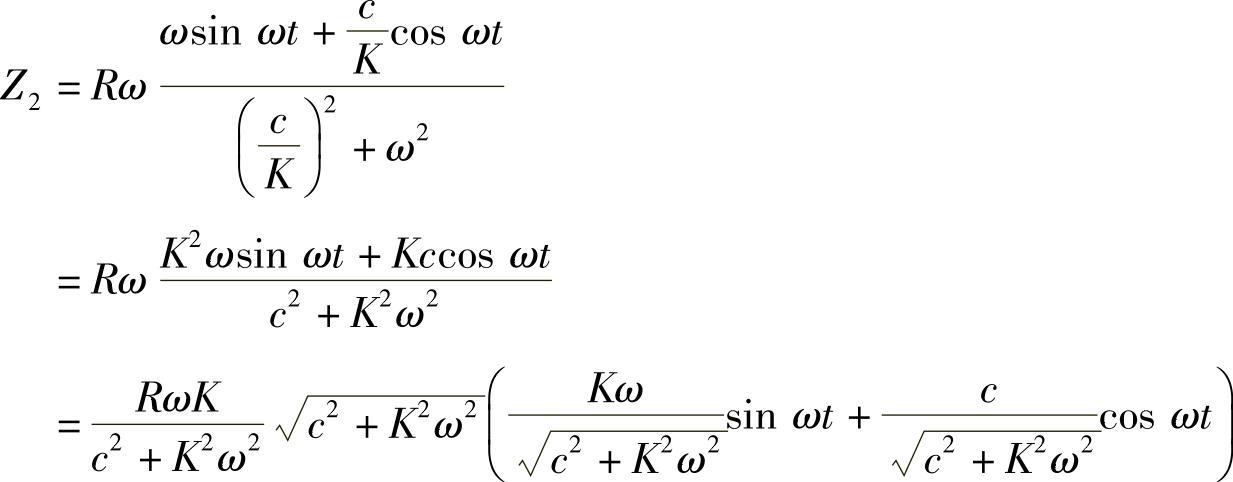
若令

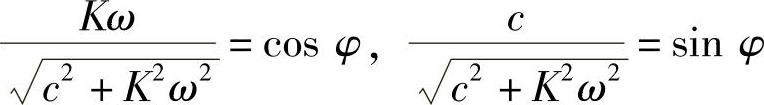
则

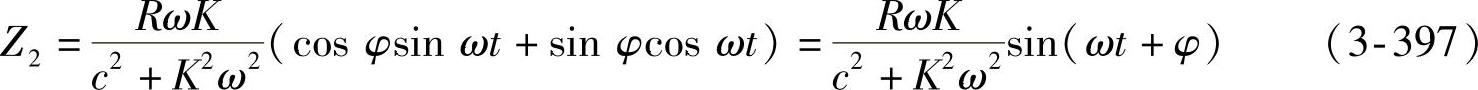
由于

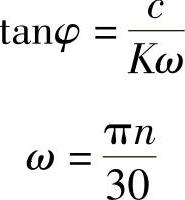
于是有

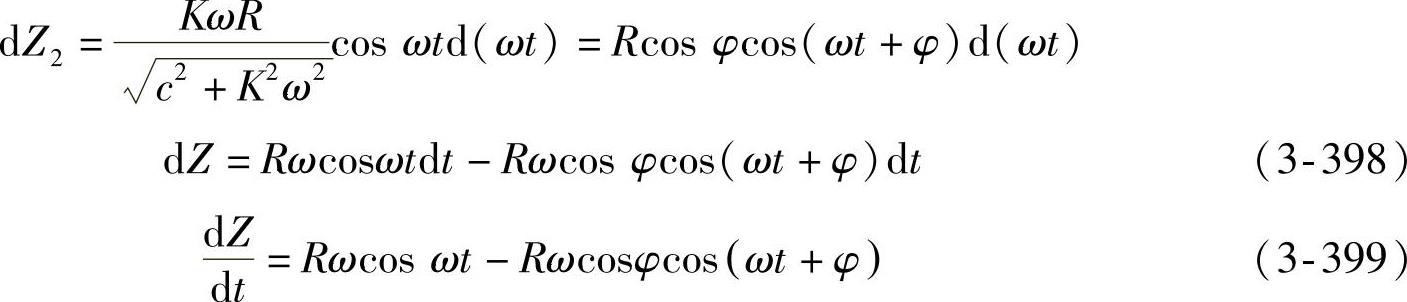
令，可解得

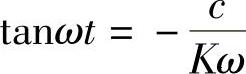
即

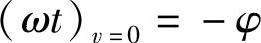
再令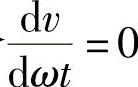，又求得

cot ωt=tanφ

d²v

=Rω{cos φcos（ωt+φ）-cos ωt}<0（dωt）2

所以v′=0时的相位值是v获得极大值的点，即时，活塞相对于缸筒的速度达到极大值，为

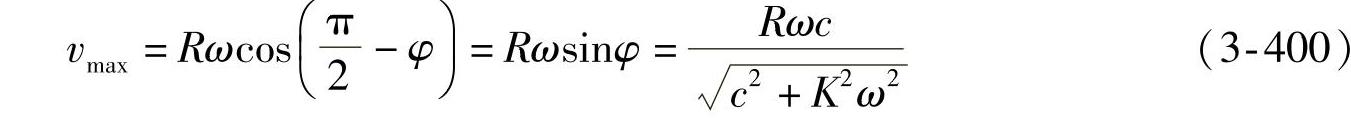
活塞相对速度由0变到最大值的相位角为

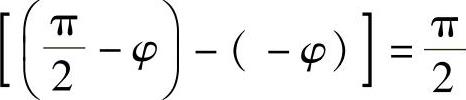
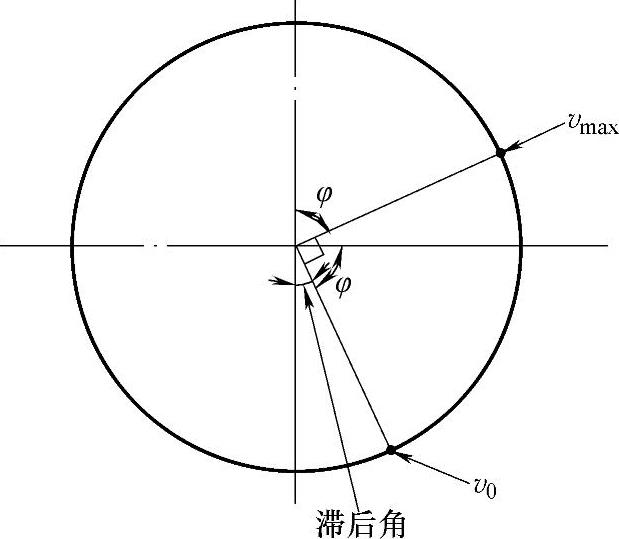
图3-141 相位角与滞后角

这是符合规律的。由于阻尼等因素的影响，活塞相对速度与曲柄机构的运动关系滞后了一个角度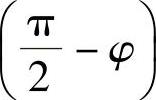，如图3-141所示。显然，φ值越大，滞后角就越小，而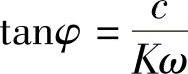，故滞后角和扭杆刚度c成反比，与试验台的角速度ω及阻尼系数K成正比。

既已找到了活塞相对于缸筒的最大速度，那就可回过头来从理论上推求特定值法的阻尼系数了。

因为

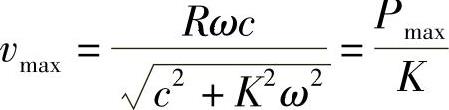(www.daowen.com)

解此方程便可得

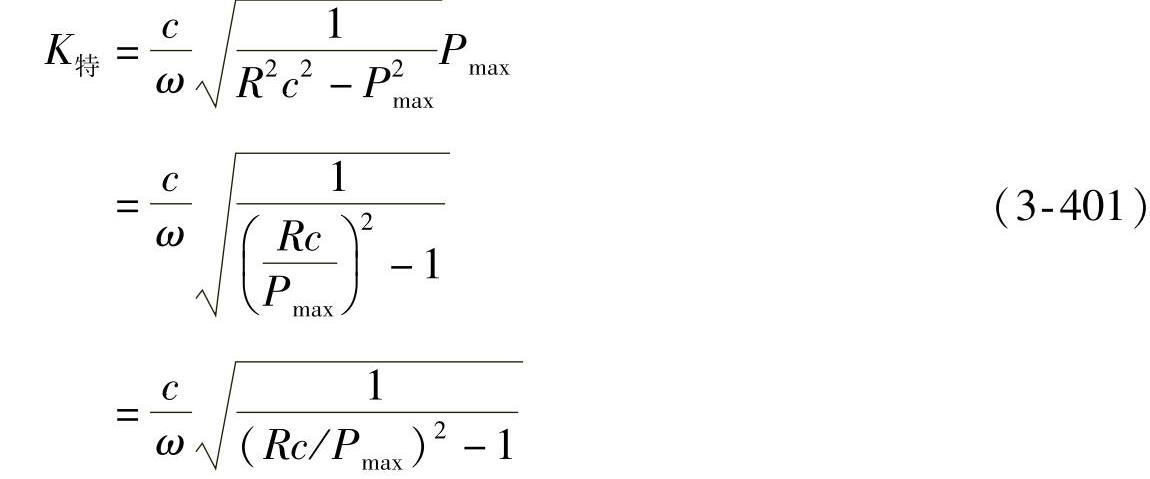
由式（3-401）可见，这种试验台所能测的最大力，不能超过曲柄半径和换算线刚度之积，即

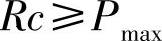
下面根据图3-142来推求扭杆的换算线刚度c。设Kφ为扭杆的扭转刚度。从材料力学可知

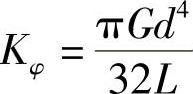
式中 d——扭杆的直径；

L——扭杆的有效长度，如图3-139所示（图示为扭杆半长l）。

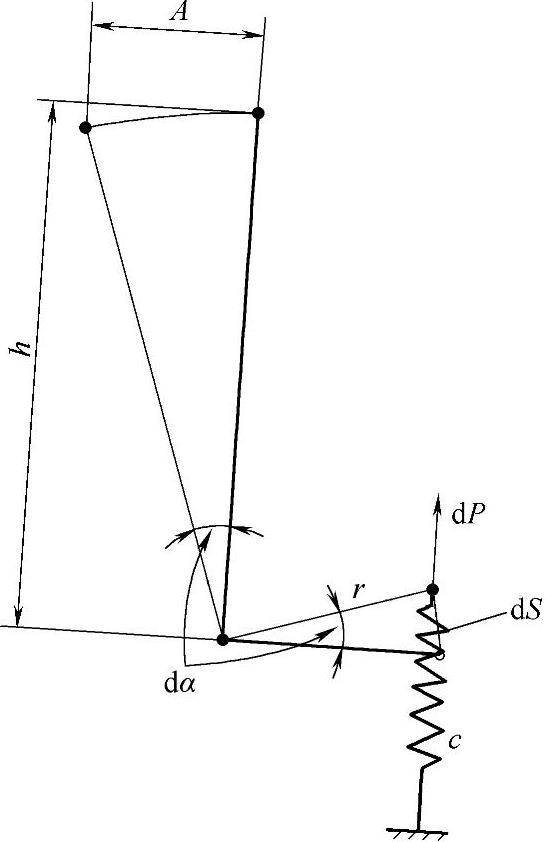
图3-142 扭杆的换算刚度

按照扭转刚度的定义，有

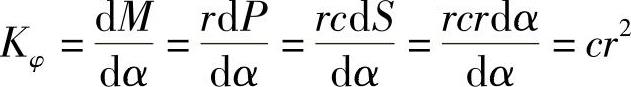
故

式中 r——扭杆弹簧臂的长度。

附带推求一下校正系数α_校与换算线刚度的关系。按定义，校正系数是作用在扭杆弹簧臂端点上的造成画针端点横向单位位移的纵向力。因此有

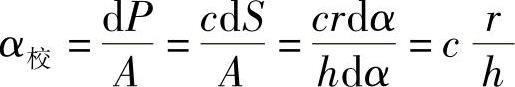
所以有

2）P-v图法。

所谓P-v图法，就是阻力-速度特性曲线法，如图3-143所示。

由特定值法可知，根据示功图可确定最大阻力，以及活塞的相对行程S，再根据试验台的转速，又可算出相应的最大速度，一张示功图便可在坐标系上定出两个点来。每一张示功图不仅和给定转速相对应，而且和曲柄的长度R=S₀/2的大小有关系，在同一试验台上，若逐次改变曲柄的长度便可画出一族示功图来，如图3-144所示，从而便可找到若干个阻力随速度变化的点了。把这些点连接起来的曲线便是阻力-速度特性曲线。这条曲线的斜率就是减振器的阻尼系数，即

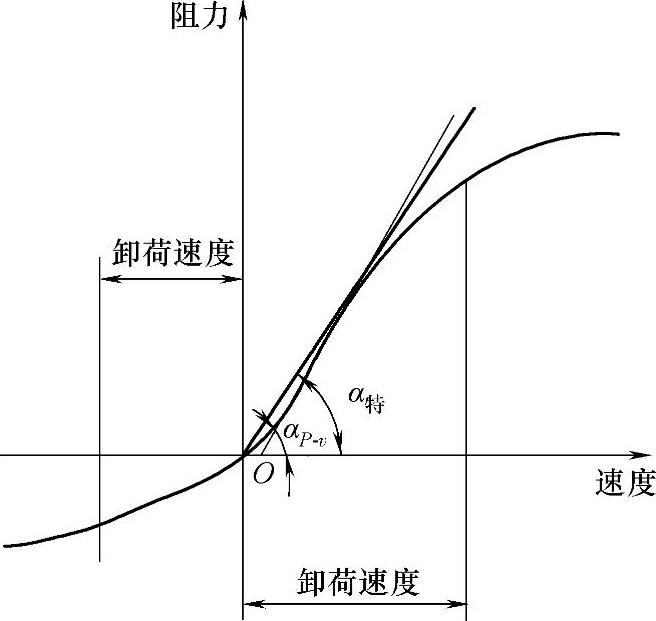
图3-143 阻力-速度特性

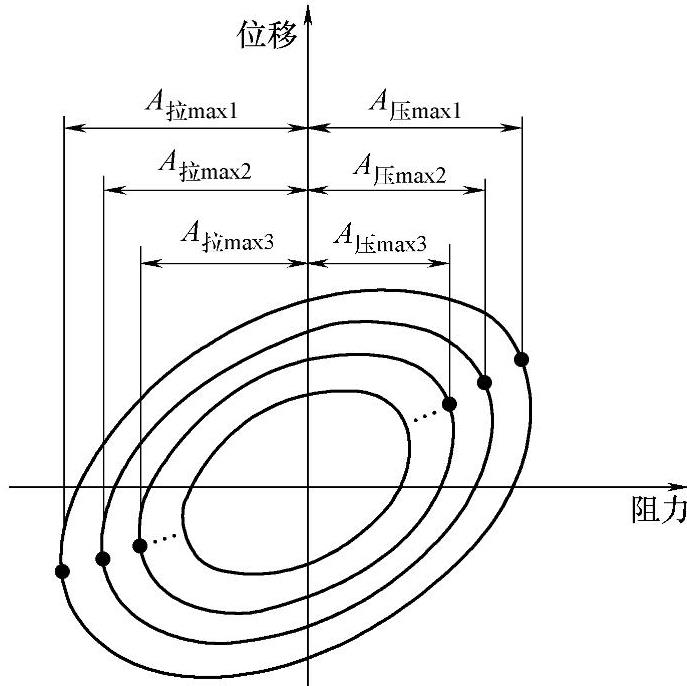
图3-144 示功图族

3）平均值法。

所谓平均值法，就是利用示功图的面积F，找出平均阻力P_平，再根据试验台的工作原理，推算出活塞的平均速度v_平。这两者的比值，即K_平=P_平/v_平就是按平均值法所确定的阻尼系数。

平均速度可以利用显示在示功图上的活塞的相对位移S来计算，也可以从理论上推算。因此平均值法也有几种情况。

①第一种情况。

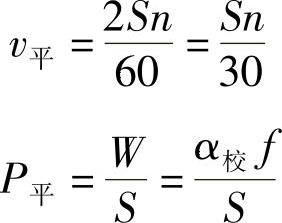
平均阻尼系数为

②第二种情况。

活塞相对速度的平均值理论上为

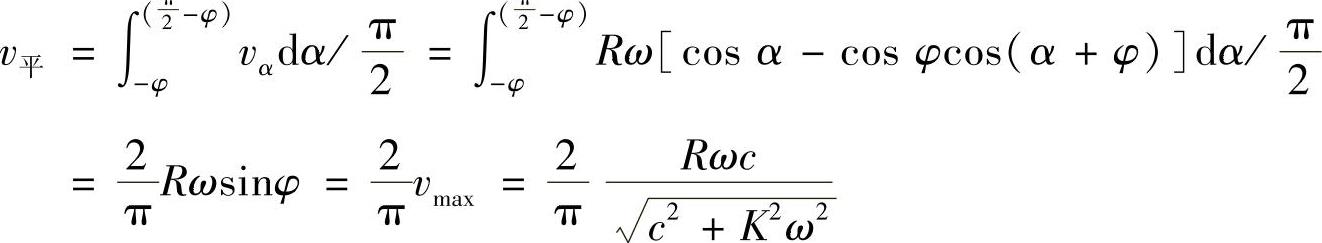
所以平均阻尼系数为

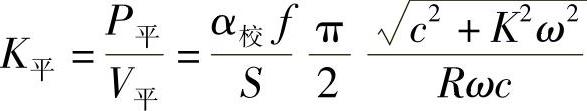
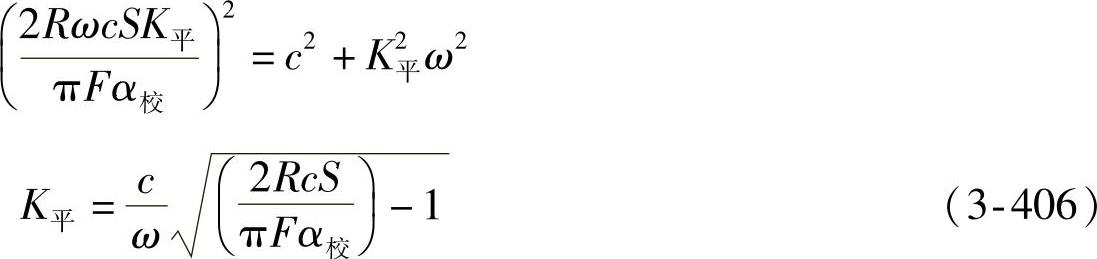
③第三种情况。

若令理论平均速度与按活塞相对位移S（显示于示功图上的）推算的平均速度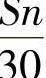相等（令最大速度相等也一样），即

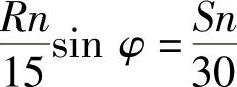
那么便有

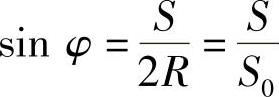
进而得

此式可用来推算出滞后角。

再由于

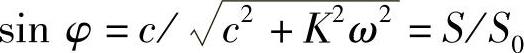
解此方程便可得

（2）三种方法的计算示例

我们曾用英国Armstrong red max4型阻力可调式减振器，在原北汽设计科试验台上画过一个示功图（图3-145）。该试验台的有关参数为：转速n=100r/min，滑块实际行程S₀=10.2cm，活塞相对行程S=8.3cm；扭杆参数：直径d=2.15cm，有效长度L=37cm，扭臂长度r=30cm，画针长度h=72.5cm。

由于该试验台扭杆的扭转刚度正反向一致（实测结果），故换算刚度和校正系数均可直接算出。

换算刚度为

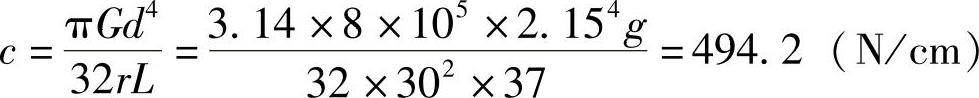
校正系数为

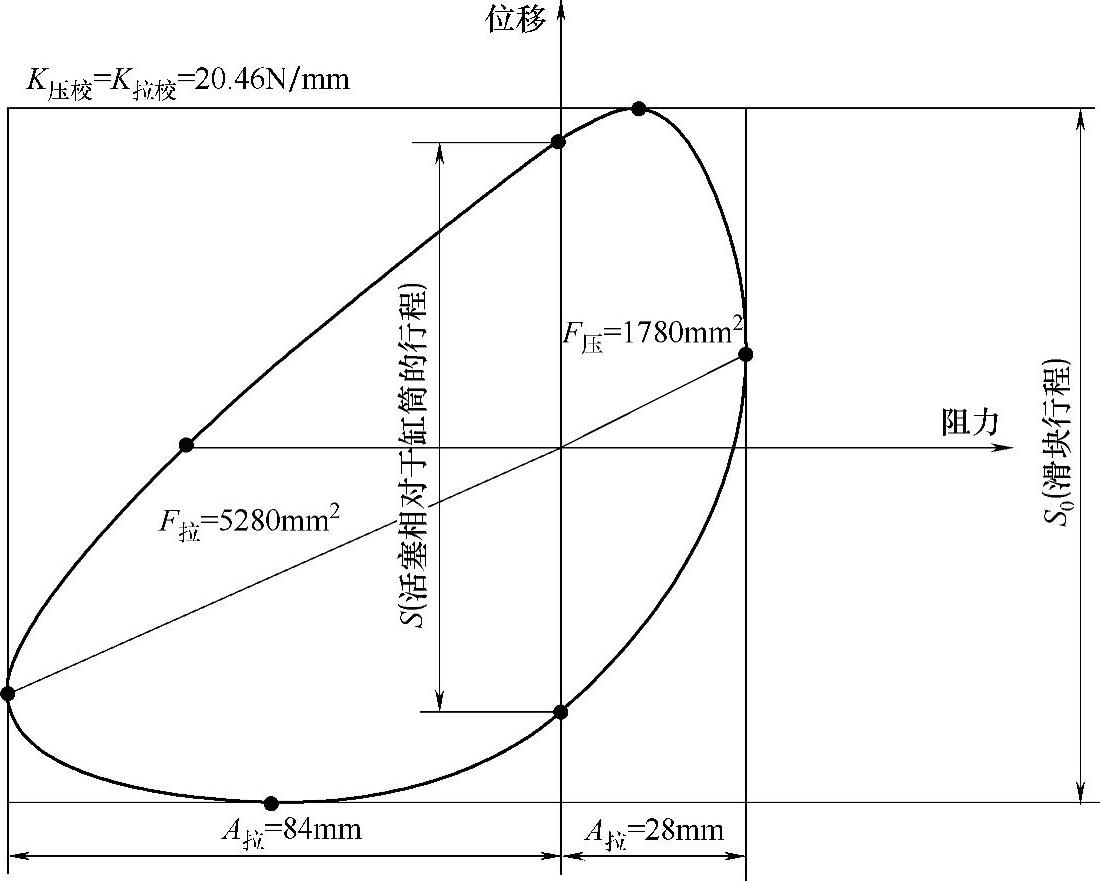
图3-145 Armstrong red max4减振器的示功图

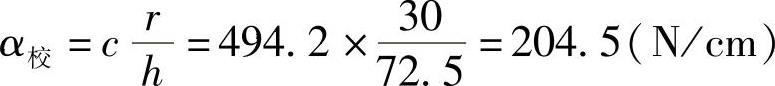
实测数据为202.9N/cm，可见误差极微小。

下面分别计算阻尼系数。

1）按特定值法。

根据式（3-392），有

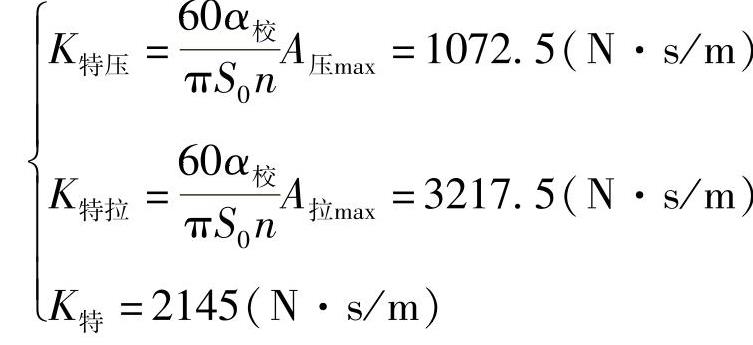
根据式（3-393），有

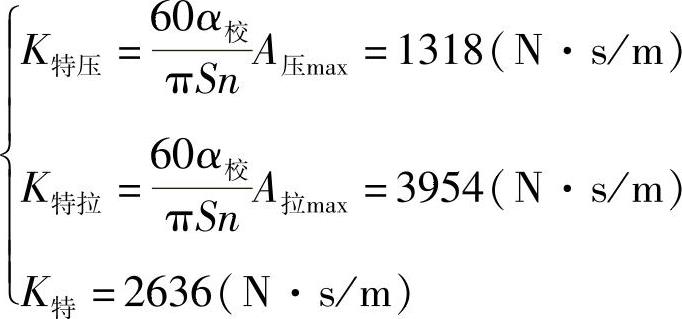
根据式（3-401），有

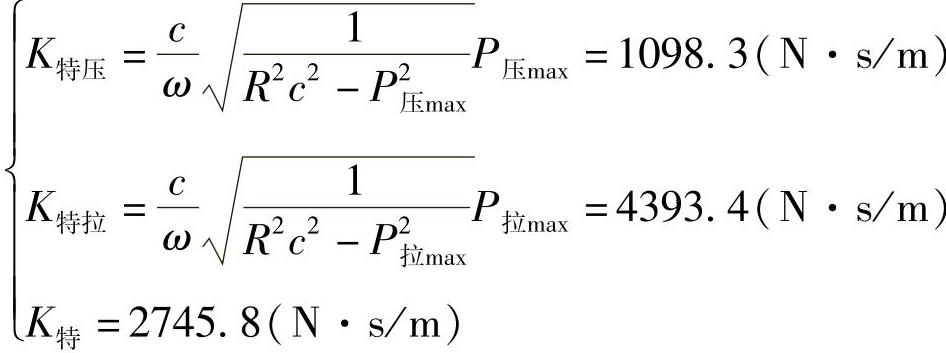
2）按平均值法。

根据式（3-405），有

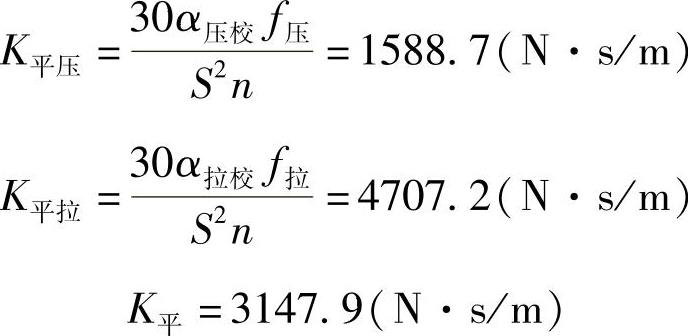
根据式（3-406），有

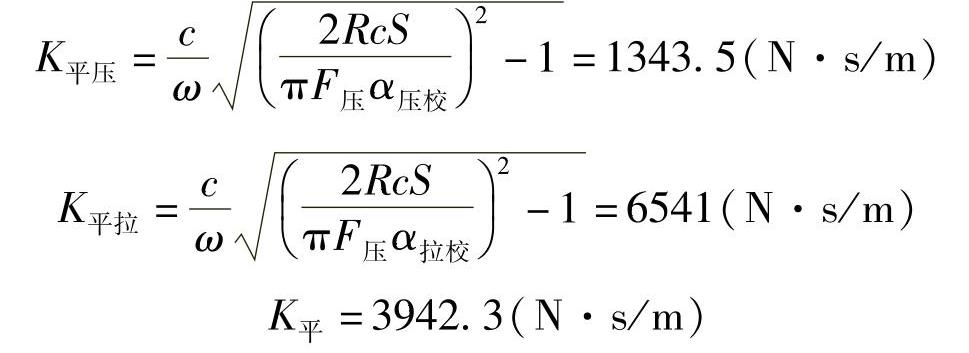
根据式（3-407），有

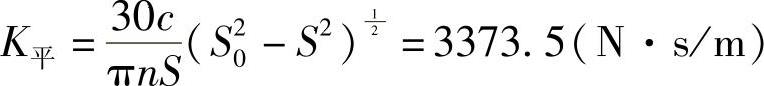
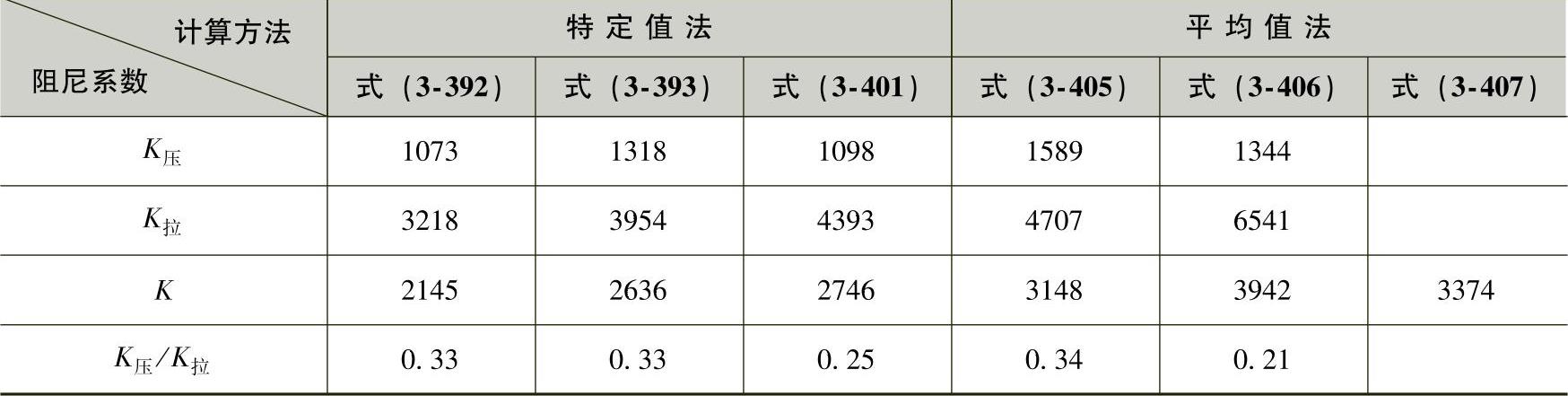
各种方法的计算结果见表3-71。

表3-71 各种方法的计算结果（N·s/m）

（3）三种方法的分析评价

以上三种方法均有一定的道理，那么，到底哪种方法更接近于实际、更适合于实用呢？通过特定值法和平均值法的计算，从表中所列数据可以明显看出：同一示功图，由于计算处理的方法不一样，阻尼系数的数值差别也很大。但若把这些数据和P-v图的趋态相对照，也不难得到如下结论，如图3-146所示。

按特定值法所确定的阻尼系数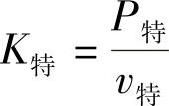，当v_特不超过卸荷速度v_卸时，是和按P-v图法所确定的阻尼系数基本一致的。作为“双百”规范的试验台和一般汽车减振器，v_特（即v_max）大于v_卸。因为

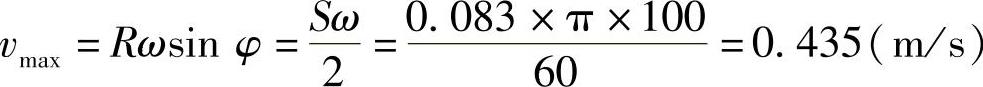
而v_卸超不过0.35m/s。所以，当v_特大于v_卸时，K_特=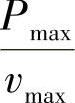，小于按P-v图法确定的卸荷之前的阻尼系数，而又大于卸荷之后的阻尼系数。

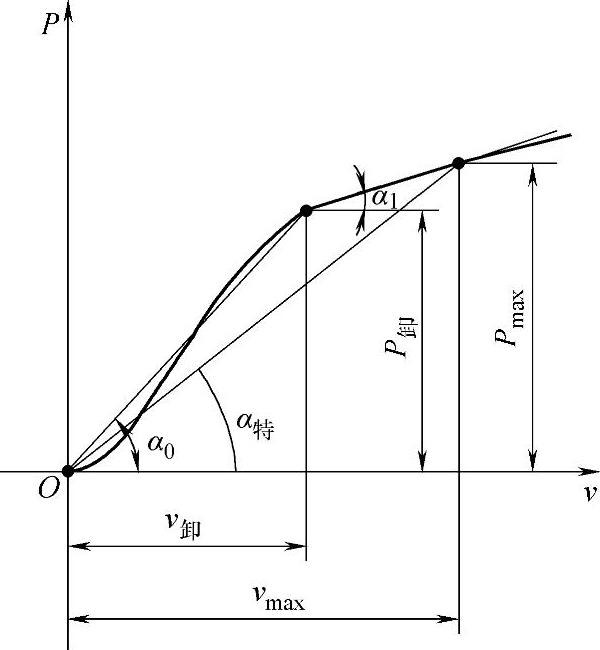
图3-146 三法对比

P-v图法较为形象地表达了阻力与速度的相互关系，表达了阻尼系数的变化趋势。从理论上讲，阻尼系数K=dP/dv是合理的。然而，曲线在每一点都有一个斜率，若近似地当作直线处理，那在实质上就和特定值法没有区别了，只不过是趋近的点多而已。况且画一组示功图较为麻烦，作为检验设计是不太方便的。

特定值法只是孤立地考虑一个点，而忽视了示功图的全面的实际情况。平均值法则不同：在第一、第二两种情况中，既联系了示功图的整个面积，又考虑了速度的平均值，故用此方法确定的阻尼系数不同于前述的两种方法所确定的值。它比P-v图法卸荷前的要小，比卸荷后的要大，再由于v_max超过v_卸，所以它也必然要大于按特定值法所确定的数值。表3-71中的数值正好说明了这一情况。

减振器是装于汽车上使用的，在不少路面上的最大线速度都将超过卸荷速度。那么，设计者选择阻尼系数时到底应该选卸荷之前的，还是之后的呢？这两种情况都不能充分结合实际，所以平均值法所确定的数值描绘了全周期的情况，比较适合于实际情况。

在平均值法的第一种情况中，阻尼系数是通过令理论平均速度和按示功图上的活塞的相对位移值S所推得的平均速度两者相等来推解出来的。它完全不同于前述各种方法。前述各种方法皆未脱离P=Kv这种线性假设，尽管各种方法都不同程度地联系了示功图的实际，但又被线性假设所影响，然而，平均值法第三种情况理论成分较大，虽然联系了活塞相对位移这个实际，缺油、阀门情况等因素却未能考虑，特别是在扭杆刚度正反向一致的情况下，压、拉行程的阻尼系数就无法区分。虽然如此，该方法用来计算周期阻尼系数的平均值还是很值得参考的。

综合来看，平均值法第一种情况是比较合适的，不仅周期阻尼系数较为接近实际，而且压、拉阻尼系数也比较可信。压、拉阻尼系数比ξ作为特定值法的两种情况，也是最大力之比，即

作为平均值法，它是总功之比，即

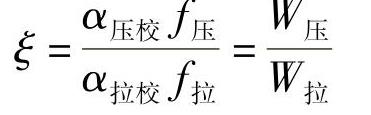
至于其他方法所得出的阻尼系数比，还需进一步研究。