稳态转向特性是汽车操纵稳定性的主要方面,而影响稳态转向特性的因素也很多,转向系统的侧倾牵动、转向系统与悬架的运动干涉、弹性车轮的侧倾偏离(包括负荷分配和角刚度比等)、悬架导向杆系的侧倾牵动及地面切向反力的影响等。
实践证明,上述因素对转向特性的影响并非是等量齐观,而是有轻有重的。例如,悬架导向杆系的牵动只有理论上的意义,在0.4g侧向加速度的作用下,带来的轴偏角不会超过0.5°。然而,有的因素却是不可忽视的,例如,转向机构在0.4g侧向加速度的作用下,不少车辆的轴偏角可能达到5°以上。特别值得指出的是,当改动侧倾中心的高度之后,不仅可以改变侧偏角的大小,而且可以改变转向特性的性质。这是改善操纵稳定性最为有效的措施,是应首先考虑的结构因素。因此,本书着重研究了三段式梯形机构在高、低侧倾中心两种情况下是如何影响汽车操纵稳定性的。
(1)机理及基本假设
1)机理。
三段式梯形机构如图3-116所示,其中点A为转向机与转向摇臂的连接点,AB为转向摇臂,DE为梯形臂,点E为与主销连接点。注意:A、B、C三点置于车身之上,D、E两点位于车轮之上。
三段式梯形机构是如何影响汽车的转向特性的呢?汽车车身(悬挂质量)因汽车转弯而受到一个侧向加速度的作用,因此便绕着侧倾轴线转过一个α角。置于车身之上的点C便绕着点C所在平面的侧倾中心O′点转过一个α角,如图3-117所示,进而通过CD杆牵动转向梯形臂DE绕着主销中心点E转过一个Δθ角,如图3-118所示。转向节臂转过Δθ角,即转向车轮产生了一个附加偏转角Δθ。左、右车轮附加偏转角的均值便是轴偏角。
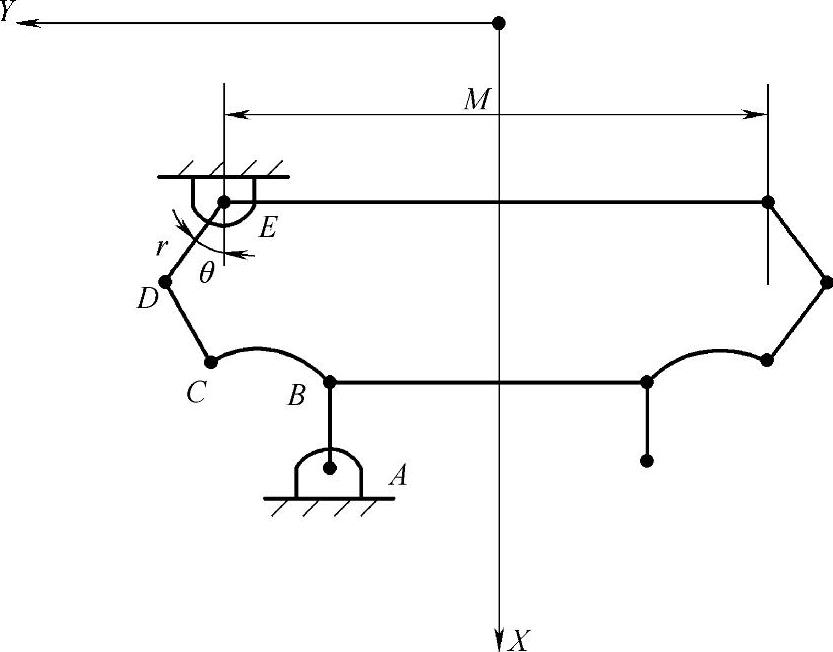
图3-116 三段式梯形机构
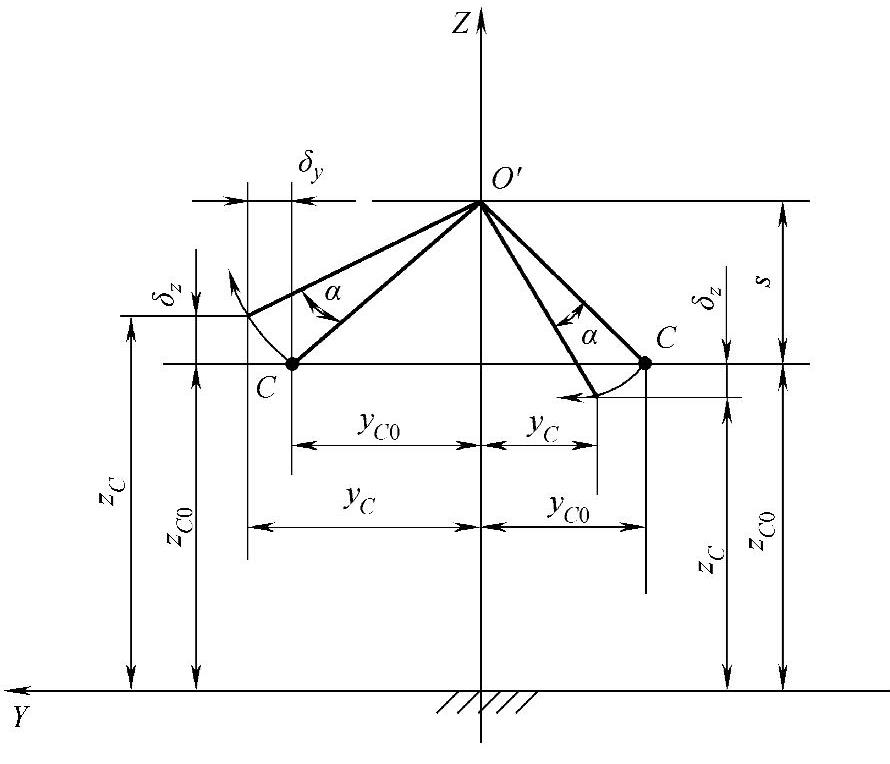
图3-117 点C绕点O′转动
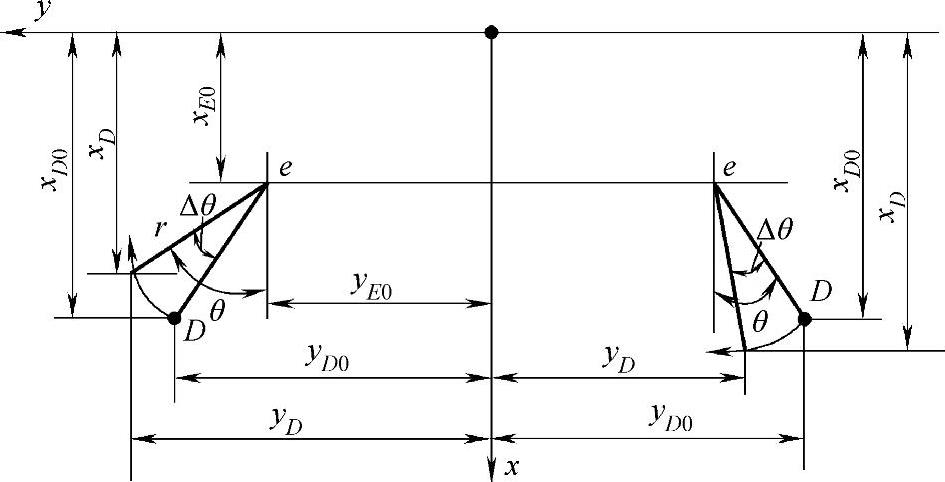
图3-118 转向节臂的转角(轮偏角)
这个轴偏角的方向,如果与汽车的转弯方向一致,便是过多转向趋势;如果与汽车的转弯方向相反,便是不足转向趋势。
2)基本假设。
①设C、D、E三点的原始坐标为
点C:xC0,yC0,zC0;
点D:xD0,yD0,zD0;
点E:xE0,yE0,zE0;
②设C、D、E三点位移后的新坐标为
点C:xC,yC,zC;
点D:xD,yD,zD;
点E:xE,yE,zE;
③设转向节臂绕点E转动时,Z轴坐标保持不变。
④设r为转向节臂在xy平面上的投影,其值为
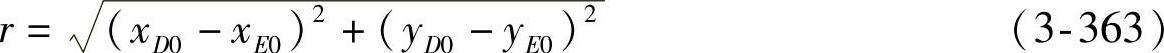
⑤设θ为转向节臂与x轴的夹角,其值为

⑥设S为侧倾中心O′的Z坐标与C点Z坐标的差,而O′为过点C的yz平面与侧倾轴线的交点,因此有

下面将对高侧倾中心(点O′高于点C)和低侧倾中心(点O′低于点C)两种情况下的左、右轮偏转角Δθ与车身侧倾角α的函数关系分别建立计算模型。
(2)计算模型的建立
1)高侧倾中心情况。
①左轮偏转角。由于梯形机构上的点C是悬置于车身之上,因此,当汽车左转弯时,车身在侧向加速度j的作用下,便向右倾斜,而处在左侧的点C便绕侧倾中心O′向左上方转移,如图3-117所示。点C与转向节臂端点D是由一长度恒定的杆与之相连的,因此,点D便以点E为圆心、r为半径顺时针转过一个Δθ角,如图3-118所示。Δθ角就是左轮偏转角。Δθ角的方向与汽车转弯方向相反,故此种情况为不足转向趋势。
下面具体推求Δθ=f(α)的关系式。
●C、D两点间的杆长l:C、D两点间的杆长保持恒定,其长度为
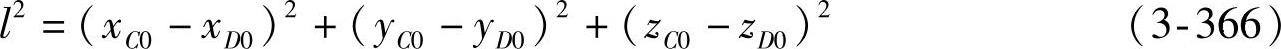
●点C位移后的新坐标:由图3-117可知点C的新坐标为

式中 α——车身侧倾角(rad)。
●点D位移后的新坐标:由图3-118可知,点D的新坐标为
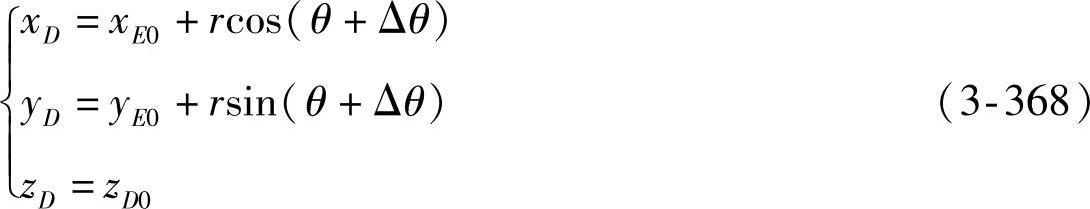
式中 Δθ——左轮偏转角;
θ——转向节臂的初相角(°)。
●Δθ=f(α)的关系式:C、D两点间的杆长恒定为l,故有
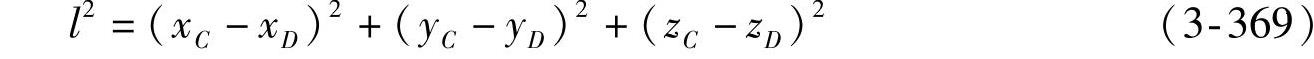
将式(3-366)、式(3-367)和式(3-368)代入式(3-369)后,可得
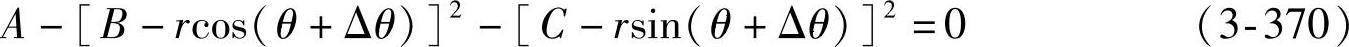
式中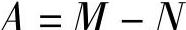
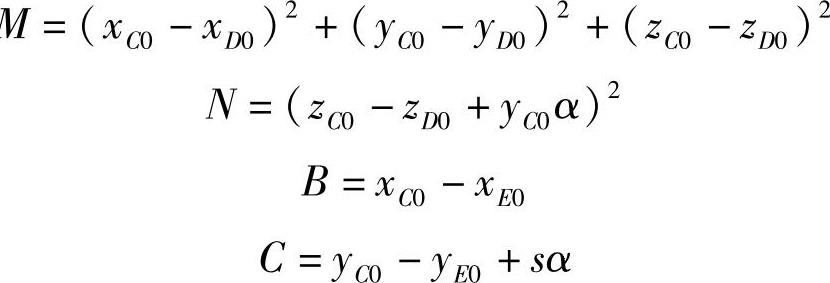
②右轮偏转角。当汽车左转弯时,右侧的点C便绕侧倾中心O′向左下方转移,从而通过CD杆牵动转向节臂顺时针转过一个Δθ角(图3-117和图3-118)。Δθ角的方向与汽车转弯方向相反,故此种情况为不足转向趋势。下面具体推导Δθ=f(α)的关系式。
●点C位移后的新坐标:由图3-117关系可知,点C的新坐标为

●点D位移后的新坐标:由图3-118关系可知,点D的新坐标为
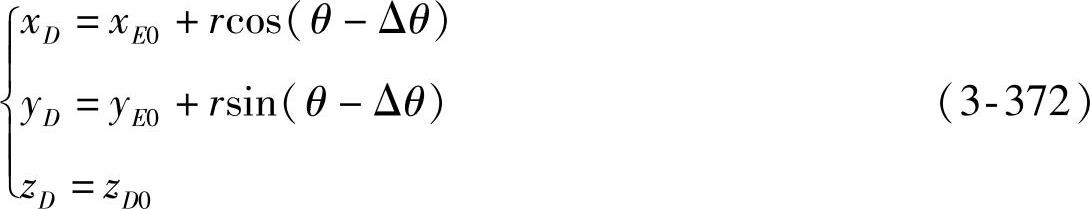
●Δθ=f(α)的关系式:杆长l恒定,故式(3-369)依然成立。将式(3-366)、式(3-371)和式(3-372)代入式(3-369)后,可得
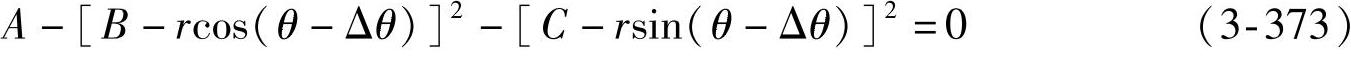
式中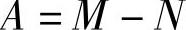
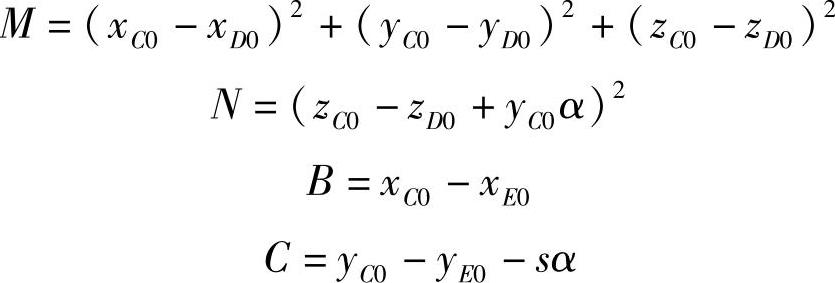
③左、右轮综合计算式。将式(3-370)和式(3-373)合并,便可得到高侧倾中心(不足转向)左、右轮侧偏角的综合计算式为
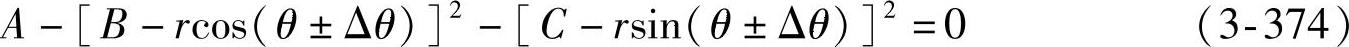
式中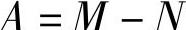
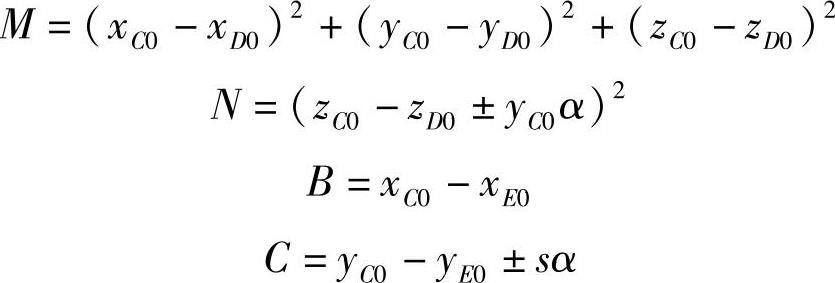
注意:式中正负号,左轮取“+”号,右轮取“-”号。z轴坐标为距地面高度,x、y轴坐标一律取正值。
对式(3-374)经进一步求解后可得高侧倾中心情况下的左右轮偏转角的显式计算式为
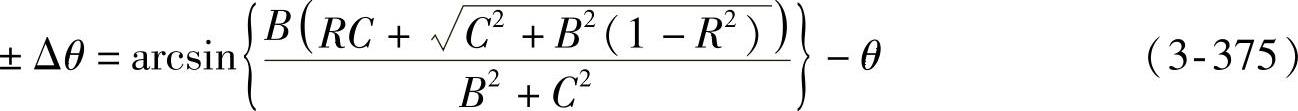
式中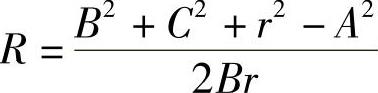

说明:
Ⅰ.z轴坐标为距地面的高度,x、y轴坐标一律取正值。
Ⅱ.式中的正负号,左轮取“+”号,右轮取“-”号。
Ⅲ.zO′为侧倾中心O′的z轴坐标,O′为过点C的yz平面与侧倾轴线的交点。α为车身侧倾角(rad)。
2)低侧倾中心情况。
①左轮偏转角。由于梯形机构上的点C悬置于车身之上,因此当汽车左转弯时,车身在侧向加速度j的作用下,便向右侧倾斜。此时处在左侧的点C便绕侧倾中心O′向右上方转移;而处在右侧的点C便绕O′向右下方转移,如图3-119所示。点C与转向节臂端点D是由一长度恒定的杆与之相连的,因此,点D便以点E为圆心、r为半径反时针转过一个Δθ角,如图3-120所示。Δθ角的方向与汽车转弯方向一致,故此种情况为过多转向趋势。
下面具体推求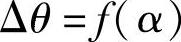 的关系式。
的关系式。
●C、D两点间的杆长l:C、D两点间的杆长保持恒定,其长度可由式(3-366)计算。
●点C位移后的新坐标:由图3-119的关系可知
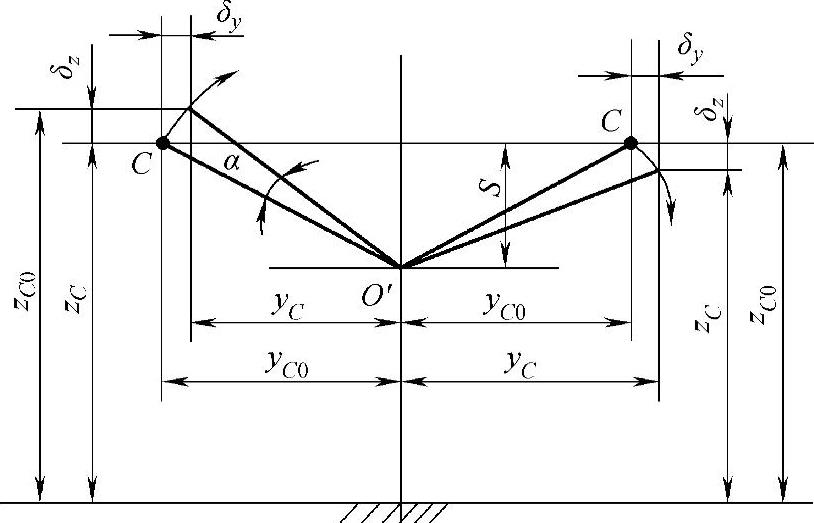
图3-119 点C绕点O′转动
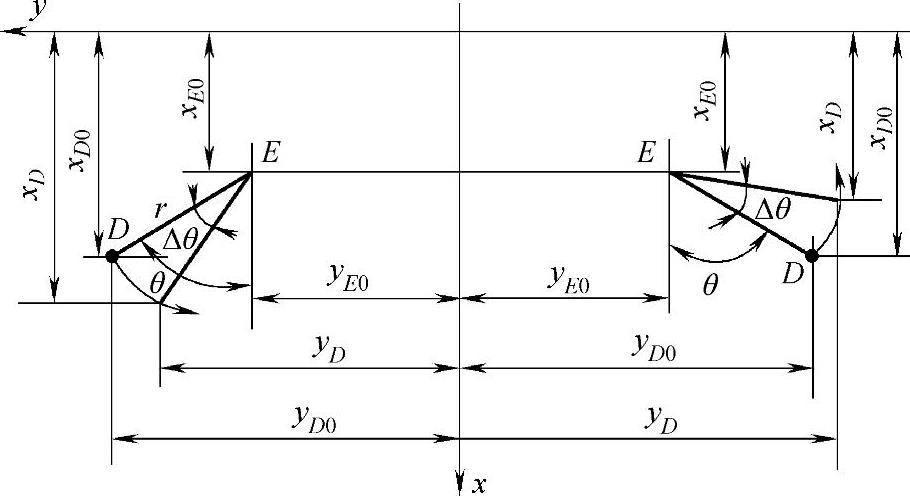
图3-120 转向节臂绕主销的转角
 (https://www.daowen.com)
(https://www.daowen.com)
式中 α——车身侧倾角(rad)。
●点D位移后的新坐标:由图3-120可知:
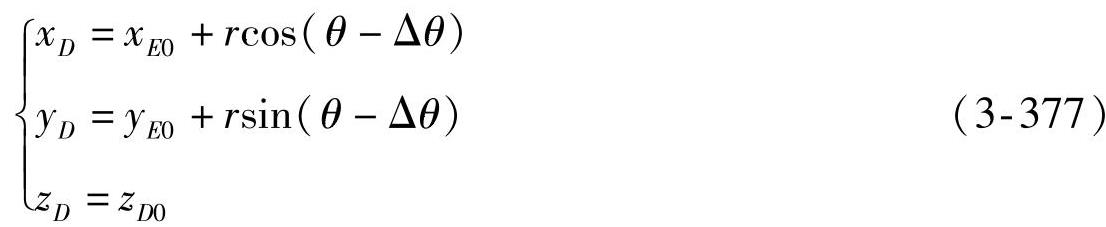
式中 Δθ——左轮偏转角(°);
θ——转向节臂的初相角(°)。
●Δθ=f(α)的关系式:由于C、D两点间的杆长恒定为l,有
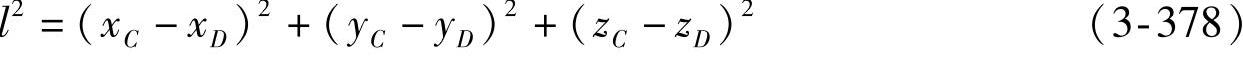
将式(3-366)、式(3-376)和式(3-377)代入式(3-378)后,可得
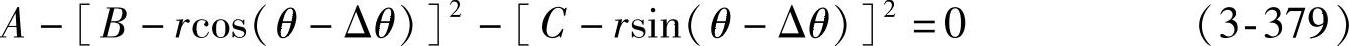
式中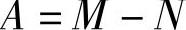
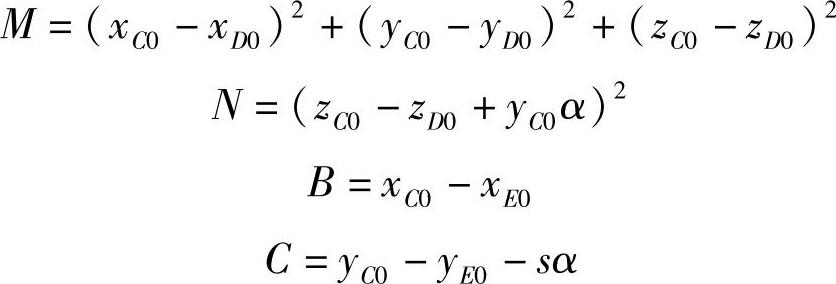
②右轮偏转角。当汽车左转弯时,右侧的点C便绕侧倾中心O′向右下方转移,参见图3-119,从而通过杆CD牵动转向节臂反时针转过一个Δθ,如图3-120所示。因为Δθ角的方向与汽车转弯方向一致,故此种情况为过多转向趋势。下面具体推导Δθ=f(α)的关系式。
●点C位移后的新坐标:由图3-119关系可知:

●点D位移后的新坐标:由图3-120关系可知:
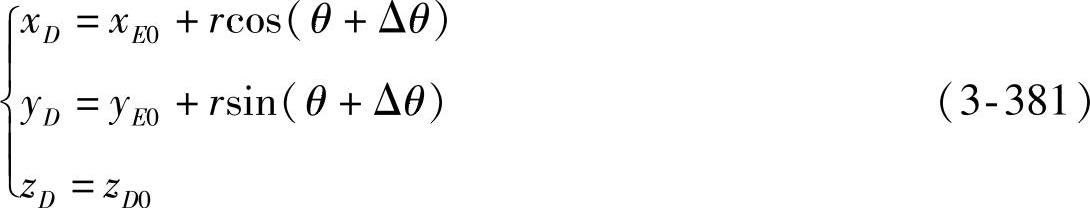
●Δθ=f(α)关系式:将式(3-366)、式(3-380)和式(3-381)代入式(3-378)后,可得
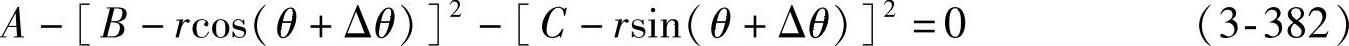
同时有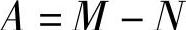
式中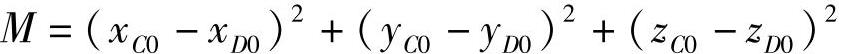
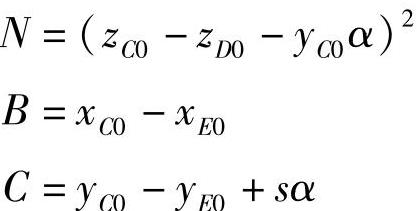
③左、右轮综合计算式。将式(3-379)和式(3-382)合并,便可得低侧倾中心(过多转向)左、右轮偏转角的综合计算式为
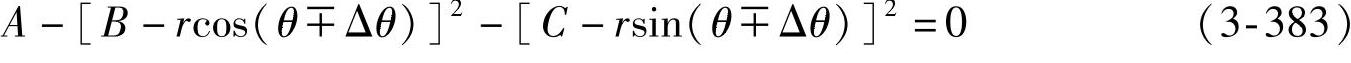
同时有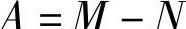
式中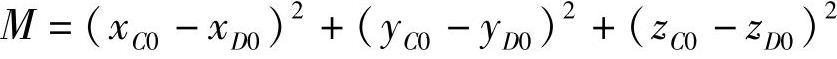
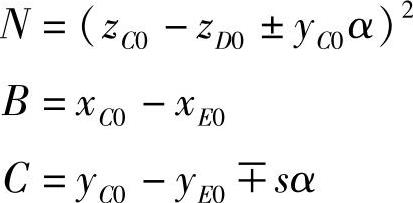
注意:式中正负号,左轮取负部,右轮取正部。利用式(3-383)还可导出左、右轮偏转角的显式计算式为
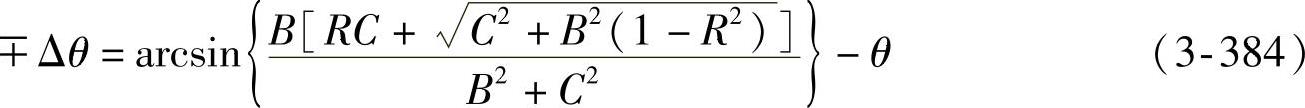
同时有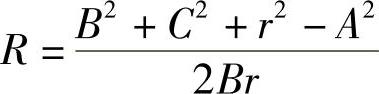
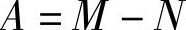
式中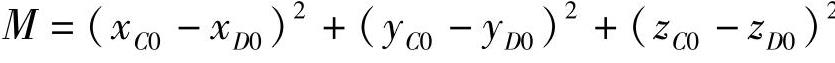
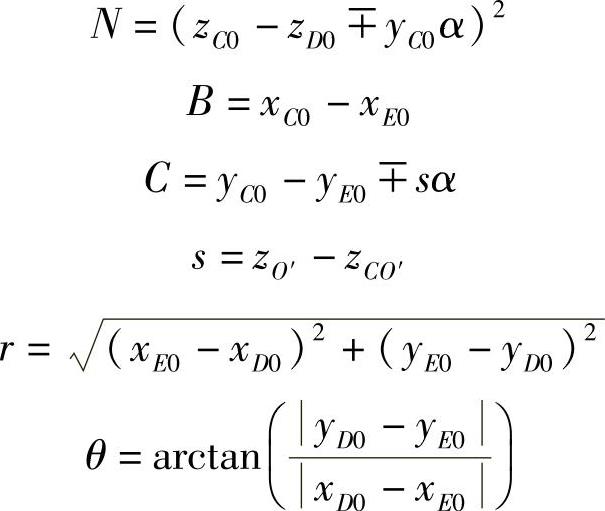
说明:
Ⅰ.z坐标为距地面的高度,x、y坐标一律取正值。
Ⅱ.式中的正负号,左轮取负号,右轮取正号。
Ⅲ.zO′为侧倾中心O′的z坐标,O′为过点C的yz平面与侧倾轴线的交点;α为车身侧倾角(rad)。
(3)计算示例
示例包括计算高、低侧倾中心两种情况以及8种车身倾角状态下的左、右轮偏转角。
1)给定参数。
①示例梯形机构各相关点的坐标见表3-67。
表3-67 示例梯形机构各相关点的坐标(单位:mm)

注:z坐标为距地面高度。
②车身侧倾角α的8种数值见表3-68。
③侧倾中心O′距地面的高度。
高侧倾中心情况:zO′=624.4mm。
表3-68 侧倾角α计算点的数值[单位:(°)]

低侧倾中心情况:zO′=349.6mm。
2)具体计算。
①用式(3-363)计算r(mm):
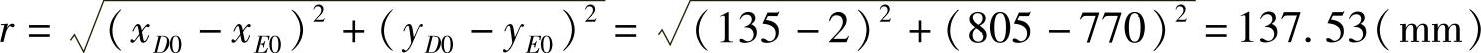
②用式(3-364)计算θ:
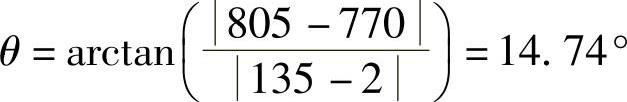
③用式(3-365)计算s(mm):
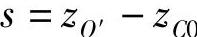
高侧倾中心情况:s=624.4-487=137.4(mm)。
低侧倾中心情况:s=487-349.6=137.4(mm)。
④用式(3-375)或式(3-384)计算A(mm)。
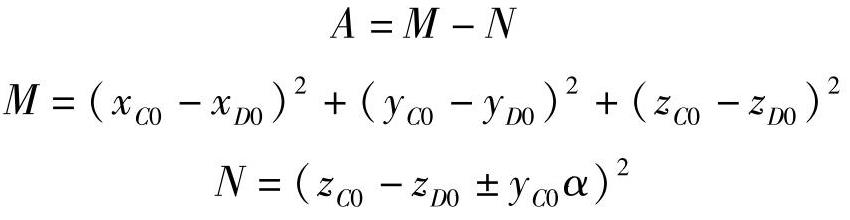
左轮:A=135989-(54+452α)2。
右轮:A=135989-(54-452α)2。
⑤用式(3-375)或式(3-384)计算B(mm)。
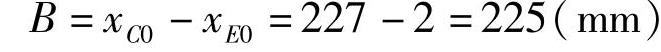
⑥用式(3-375)或式(3-384)计算C(mm)。
高左、低右:
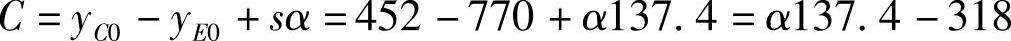
高右、低左:
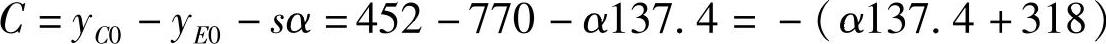
⑦用式(3-375)或式(3-384)计算R(mm)。
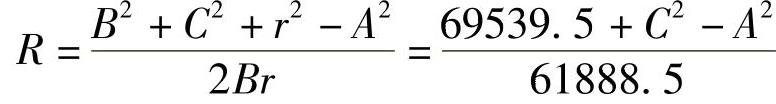
⑧用式(3-375)或式(3-384)计算Δθ。
上述计算结果,分别见表3-69和表3-70。
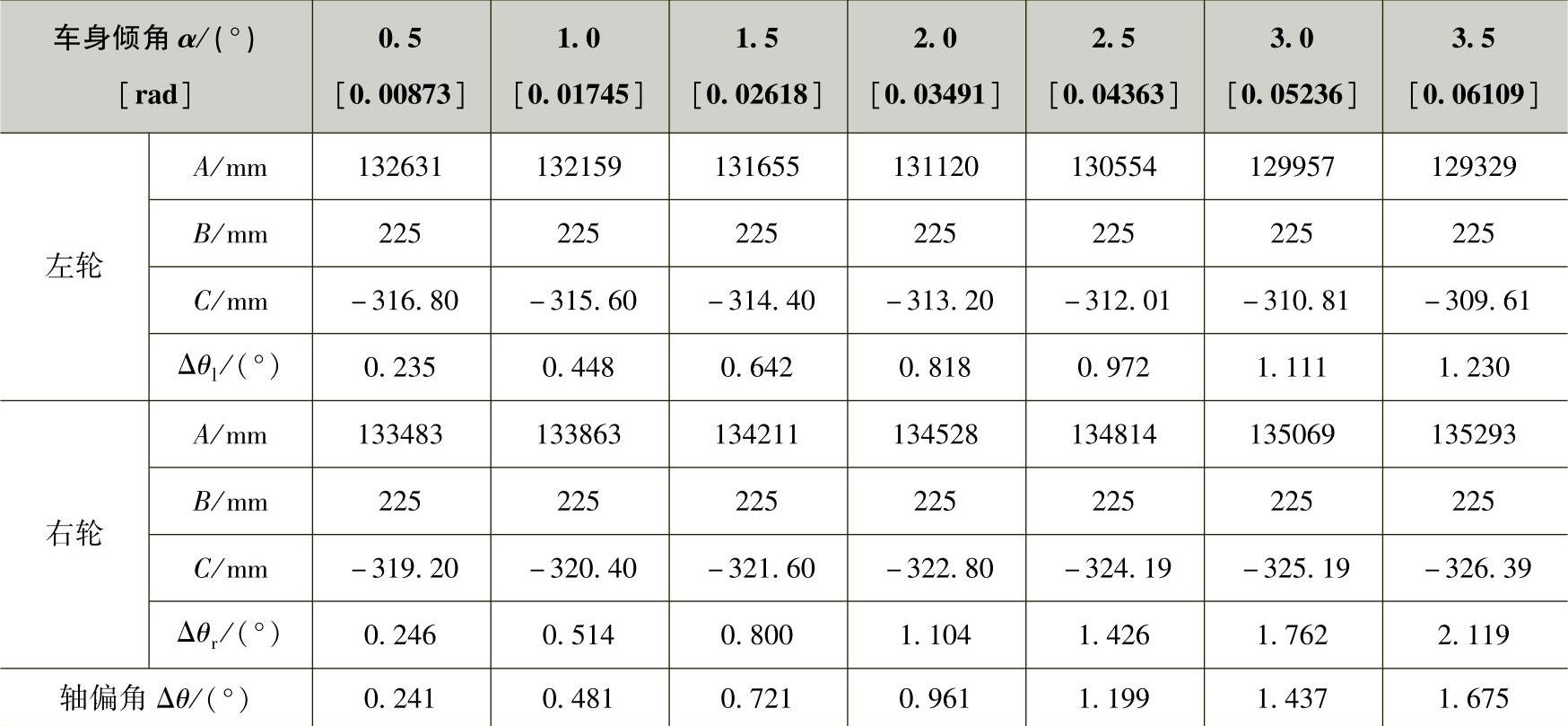
从表3-69和表3-70中的计算结果可知,轮偏角和轴偏角都是随车身侧倾角的增大而增大的。本示例梯形机构在高、低侧倾中心两种情况下的轴偏角皆为正值,说明高侧倾中心的情况为不足转向趋势,低侧倾中心的情况为过多转向趋势。此外,轴偏角的数值都是较大的,特别是低侧倾中心的情况,例如,当α=4°时,轴偏角已超过5.8°,说明其过多转向的程度十分严重。
表3-69 低侧倾中心的车轮偏转角和轴偏角
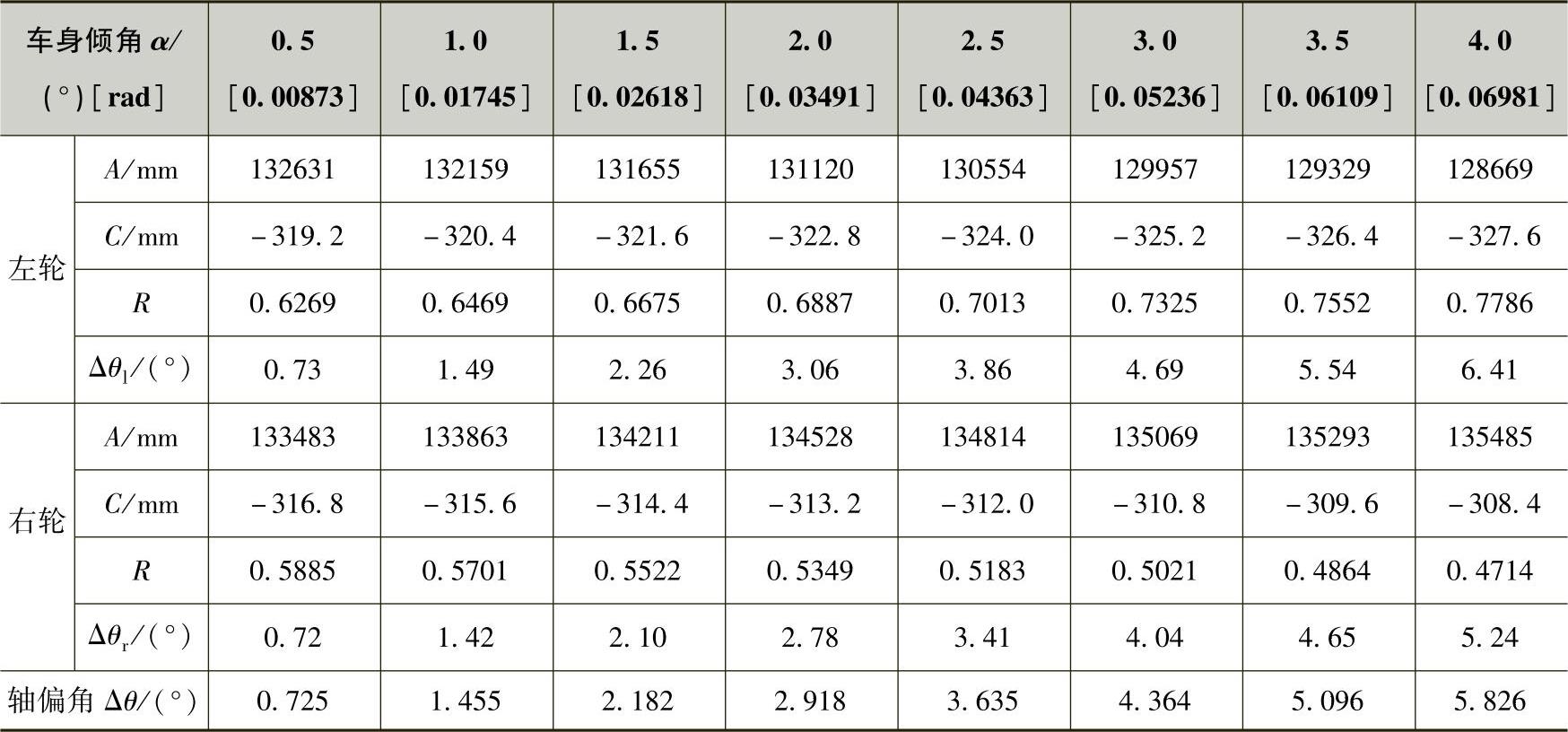
表3-70 高侧倾中心的车轮偏转角和轴偏角
(4)结论
三段式转向梯形机构是影响汽车操纵稳定性的重要系统,它与侧倾中心一起决定着转向特性的性质和程度。高侧倾中心产生不足转向趋势,低侧倾中心产生过多转向趋势。设计汽车悬架时,不仅要适当调整梯形机构的结构参数,而且特别要相对提高侧倾中心的高度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





