从普通梯形机构一节可知，根据内、外轮转角的关系，不仅可以求出整车转弯半径，而且也能掌握梯形机构的转向特性。

如何求出断开式梯形机构的内外轮转角关系呢？研究这个问题可分两步走。

第一步：假设内轮梯形臂绕主销转过一个α角，并通过保持长度不变的过渡拉杆，带动横拉杆水平位移一个距离S（或摆臂转过一个δ角），从而得到一个关系式

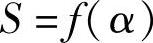
或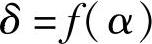

第二步：把横拉杆的水平位移S作为输入（或把δ作为输入），外轮梯形臂的转角β作为输出建立β=F（s）或β=F（δ）的关系式。这就相当于得到了β=f（α）的关系式。

具体推导过程从略，此处直接列出摆臂式和齿条式两种梯形机构的内、外轮转角关系式。

（1）摆臂三段式内、外轮转角关系（图3-114）

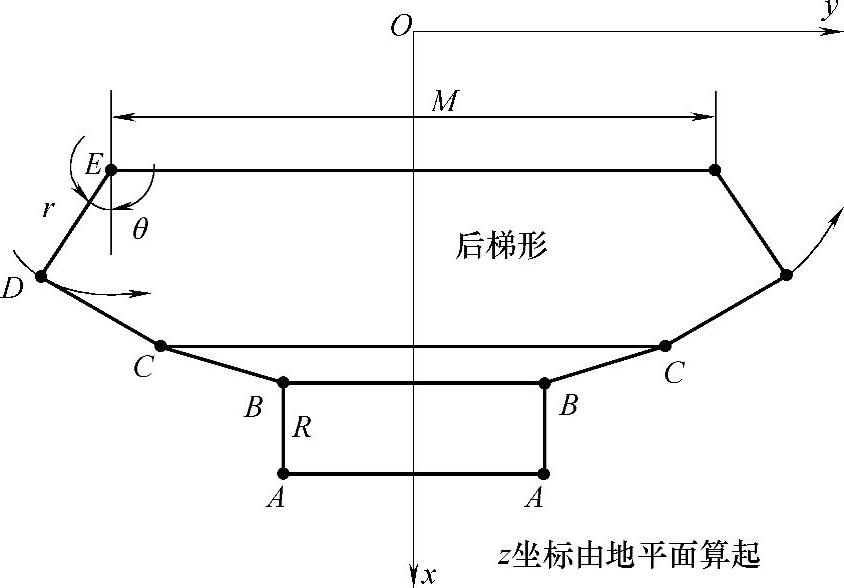
图3-114 摆臂三段式内、外轮转角关系

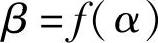
第一式：δ=f（α）

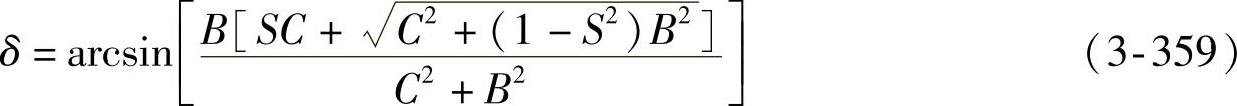
式中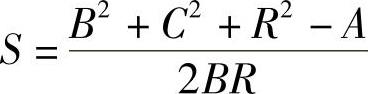

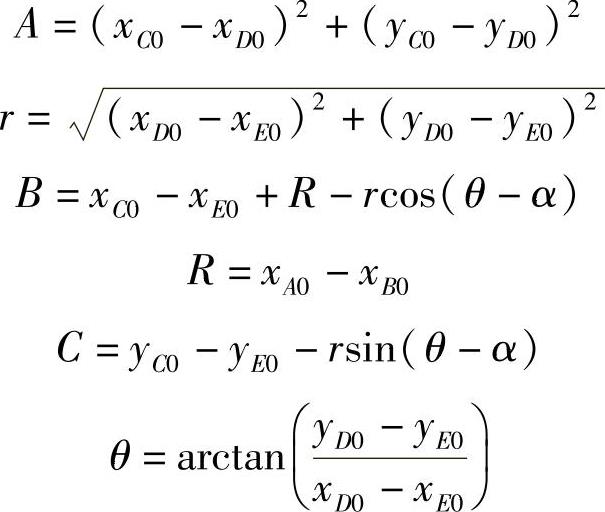
第二式：β=f（δ）

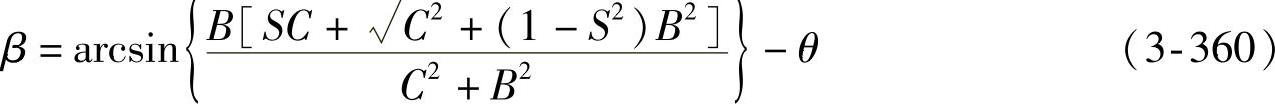
式中

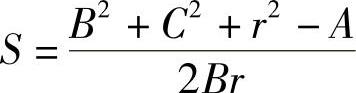(www.daowen.com)

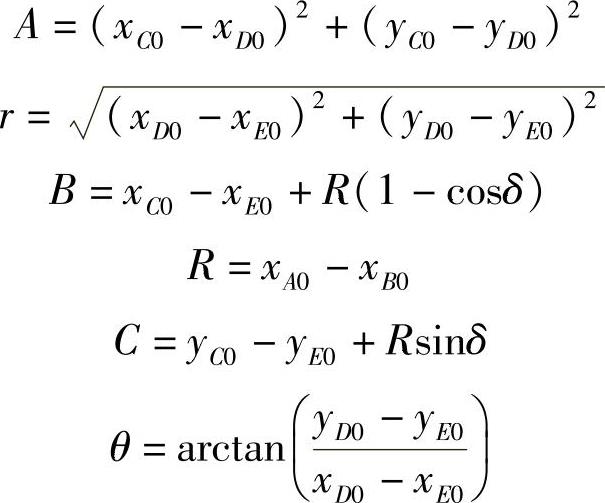
注意：

①假定梯形臂反时针转动时，D、C两点的z坐标不变。

②D、C两点间的空间杆长恒定。

③假定“C-C-B-B”刚体保持平动。

（2）齿条三段式内、外轮转角的关系（图3-115）

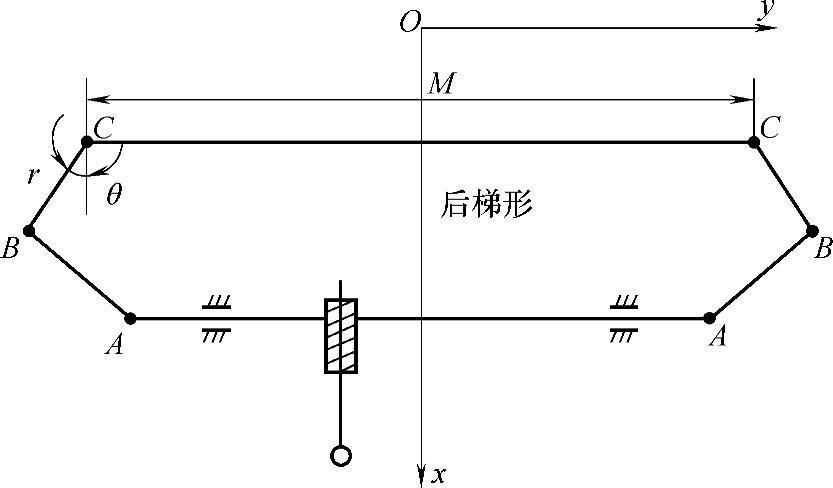
图3-115 齿条三段式内、外轮转角的关系

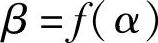
第一式：S=f（α）

式中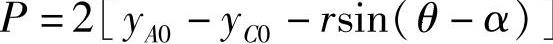

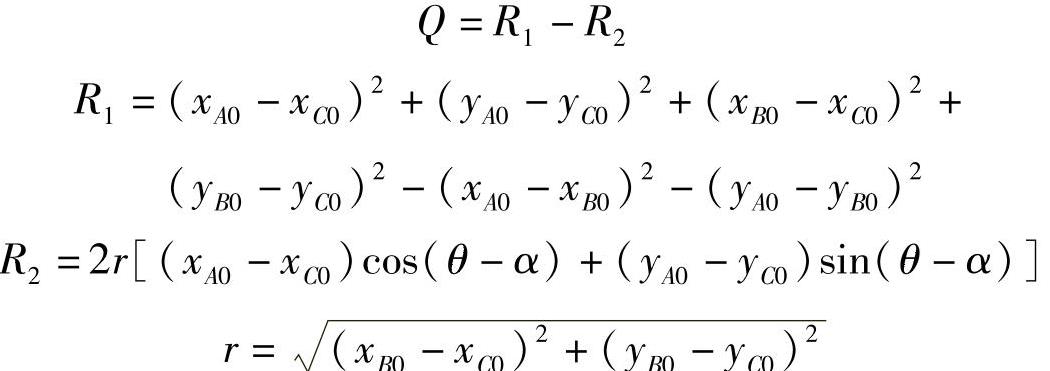
第二式：β=f（S）

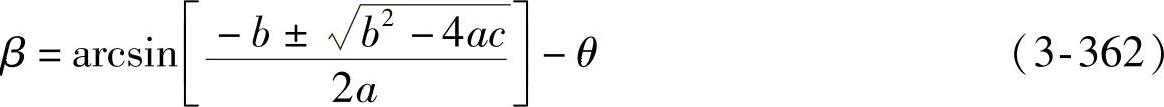
式中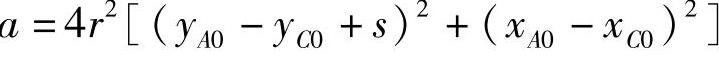

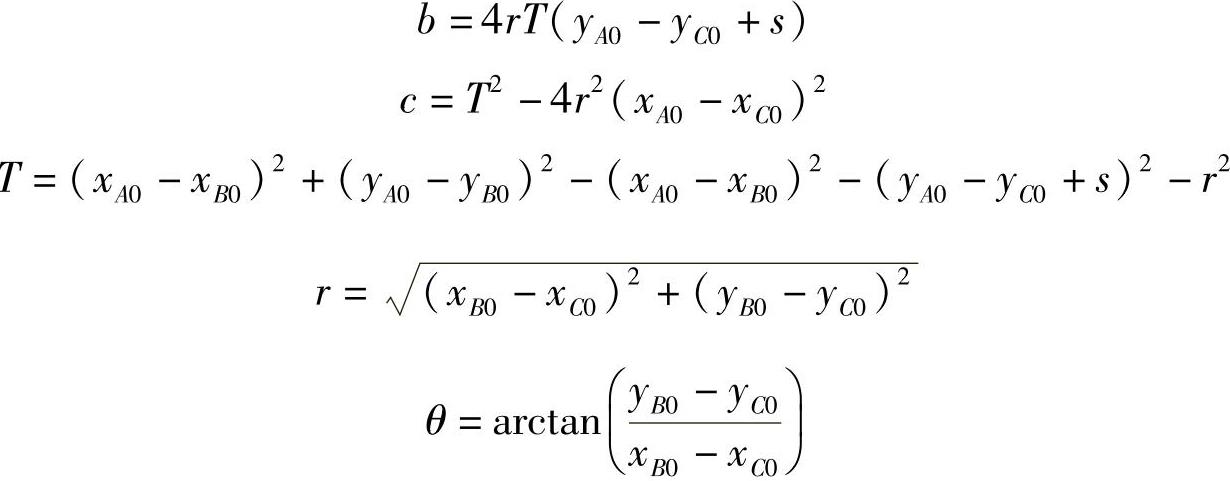
x、y、z分别为A、B、C三点满载时的原始坐标，r为梯形臂的顶视投影长度，θ为r与x轴的夹角。