转向机构附加牵动轮转向，包含两个方面的内容：一是转向系统与悬架机构运动干涉造成的车轮转向；二是垂臂球头中心绕侧倾中心转动带来的车轮转向。这些都和梯形机构相关，下面分别进行研究。

（1）转向系统与悬架运动干涉的轮转向

转向系与悬架运动的不协调性，在可逆转向系统中，当车速较低时，往往造成方向盘的摆振；而在不可逆的转向系统中，当车速较高时，必将引起转向车轮的干涉转向。

现以图3-108所示的悬架和转向系统为例来研究这个问题。

图3-108所示为摆耳在后的纵置对称板簧悬架。转向机构为方向机在车轴之后的直拉杆式。图中点O为垂臂球头中心，点M为节臂球头中心。当车身上下跳动或者侧倾时，点M既以O点为圆心，以直拉杆长度为半径划弧运动，也以点M的轨迹中心P为圆心，以点M的轨迹半径R为半径划弧运动。两者的矛盾随悬架变化量的大小而变，或者随车身侧倾角的大小而变。

假设悬架的变形量为f，且点O与点M近似地在同一纵向平面内，那么两者运动的矛盾量就是S。在同一悬架变形量的情况下，由于摆耳位置以及点O和点M的布置位置不同，矛盾量的大小也将不同，而且压缩和反弹行程也不相同。我们研究和关心的是矛盾量较大的那个行程。

如何统一这个矛盾呢？假设不考虑球头胶件的变形和克服各种间隙，矛盾量S必将转化为转向节臂和车轮的角位移，如图3-109所示。

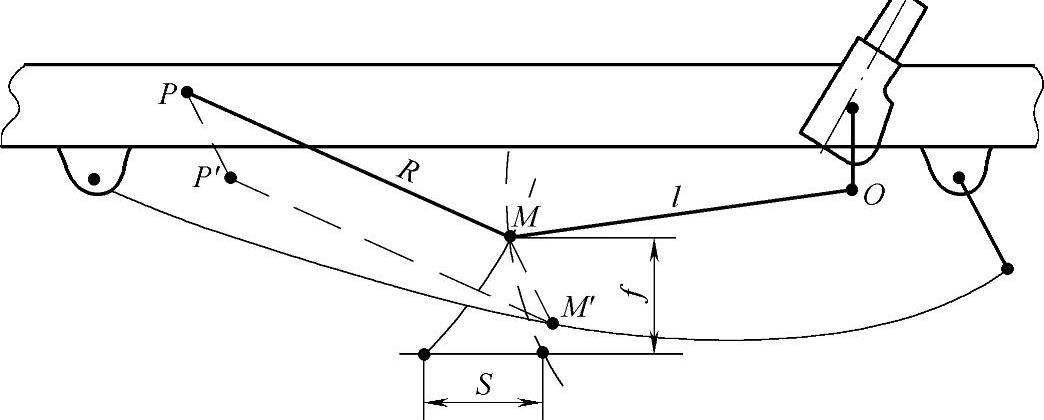
图3-108 悬架与转向系的运动干涉

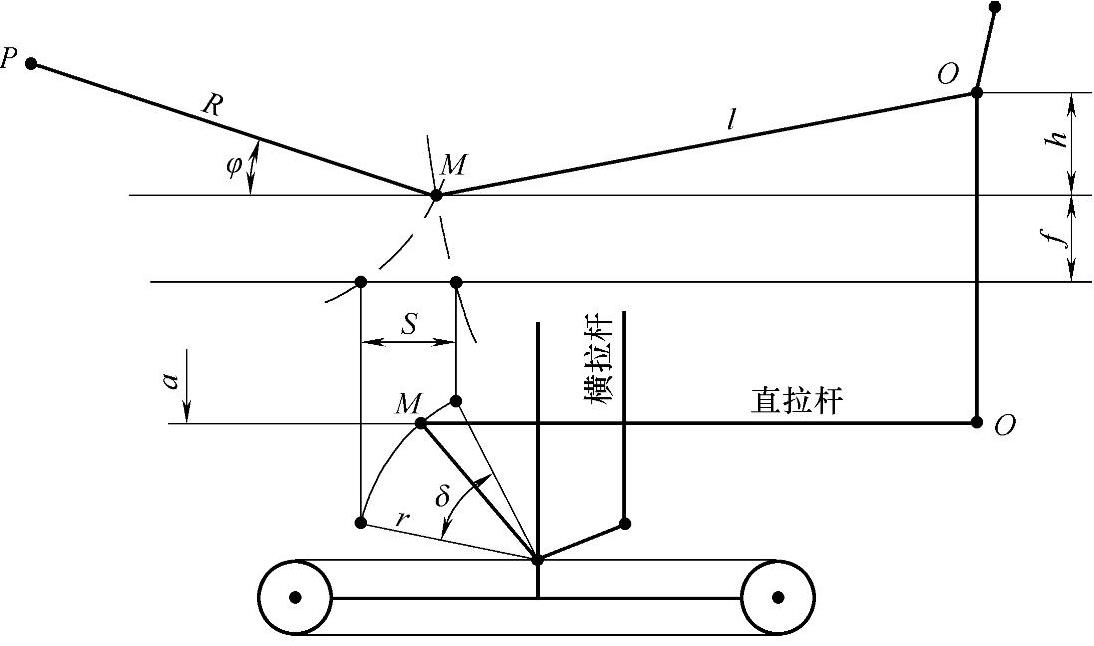
图3-109 水平位移与角位移

根据图3-109所示的几何关系，水平方向上的矛盾量S为

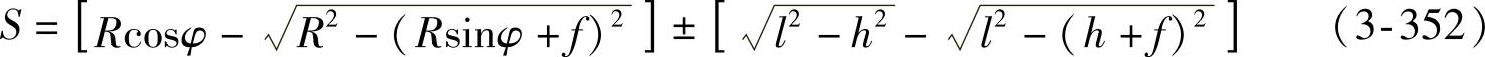
式中 R——节臂球头中心M的轨迹半径（mm）；

φ——悬架推杆角（°）；

l——直拉杆的长度（mm）；

h——l在垂直方向上的长度（mm）；

f——给定悬架的垂直位移（mm）。

f一般以车身在0.4g侧向加速度j的作用下的侧倾角θ来计算

式中 θ——车身侧倾角（rad）；

a——节臂球头中心至车身中心线的距离（mm）。

式（3-352）中的正负号，是由垂臂球头中心O的位置与节臂球头中心M的轨迹中心P的位置来决定的。如果O、P二点在车轴的异侧（图3-109），应取正号；同侧则取负号。由此可知，板簧固定吊耳与转向机同侧布置，可使运动干涉大为降低。

求出了水平方向上的矛盾量，便可算出车轮偏转角（梯形臂转角）为

式中 δ——车轮偏转角（rad）；

r——节臂长度（mm）。

轴偏角到底反映了什么转向性质呢？假设方向盘内转，车身外倾，则图3-109中的点O上提，这相当于点M下移，此时的矛盾量S需要节臂内转来统一，故此转向属于过多转向；反之，若方向盘外转，节臂依然外转，仍属过多转向。假若不转方向盘，只是车身上下跳动，此时必将造成车轮来回摆振，将导致不同转向趋势的交替出现。

（2）垂臂球头中心侧倾轮转向

汽车转向机构的形式大多数是以纵向上的直拉杆带动转向节臂转动。然而，部分汽车的转向机构却是以横向上的横拉杆带动节臂转动，进而带动梯形臂转动。BJ212越野汽车就属于这种形式，如图3-110所示。

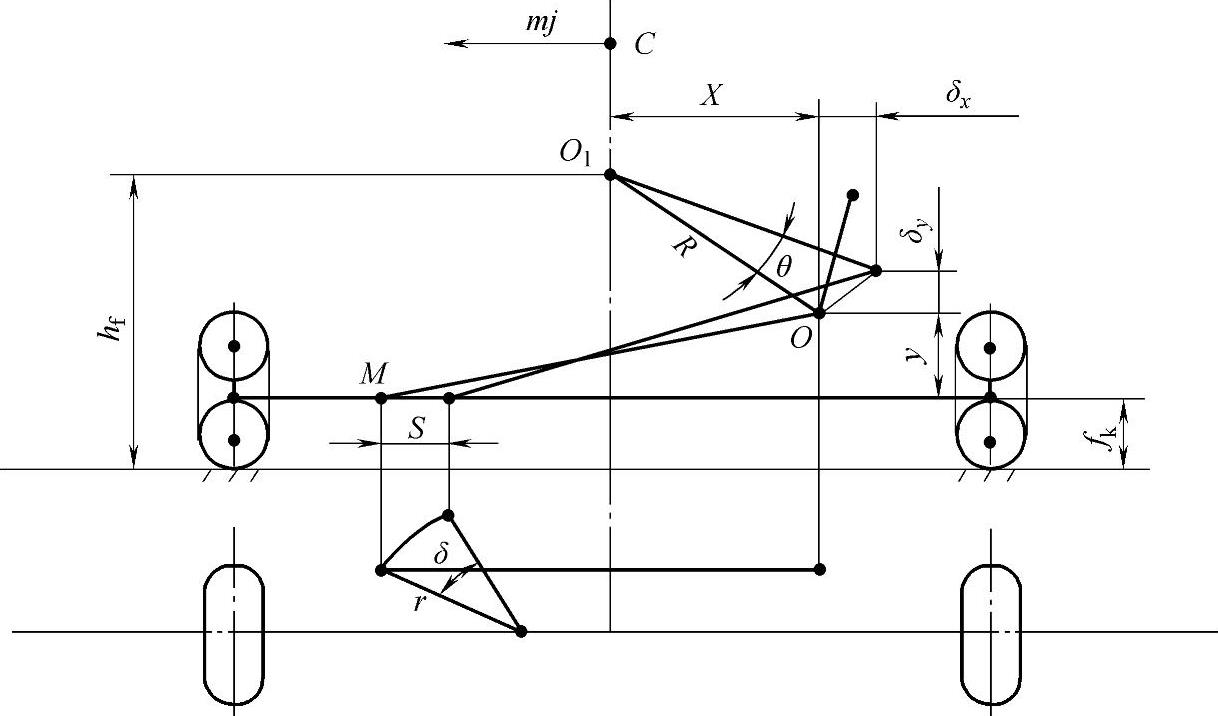
图3-110 转向机构轮转向

由式（3-354）所求出的车轮偏转角，仅是内轮偏转角，由于此偏转角较小，故可近似认为此轮偏转角就是轴偏角。(www.daowen.com)

计算示例3

示例车型为燕京YJ620型轻型客车。

该车前板簧倾角ξ=3°，固定吊耳在前，簧长L=1200mm，采用“柏林式”卷耳，满载弧高F=7mm，夹紧长度d=92mm，方向机与固定吊耳同侧。

直拉杆长度l=740mm，垂直方向投影长h=139mm，节臂球头中心至车身重心的距离a=525mm，节臂长度r=135mm。

计算推杆长度和推杆角为

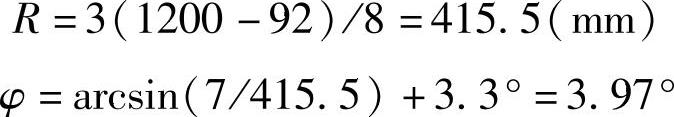
假设车身在0.4g侧向加速度的作用下的侧倾角θ=3.5°，那么由式（3-353）便可算出悬架变形量（节臂球头中心相对车身的垂直位移）为

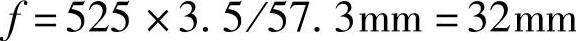
水平方向上的矛盾量S为

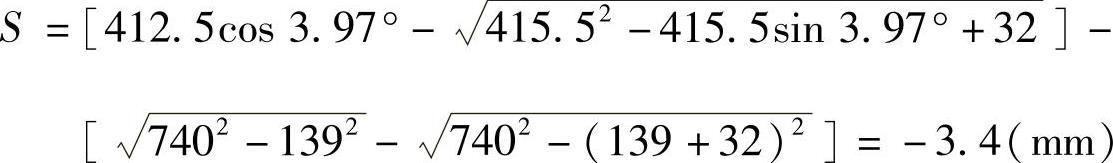
用式（3-354）计算车轮偏转角（梯形臂转角）为

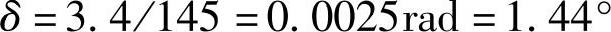
1.44°这个较小的轮偏角，说明该车型的布置方案是较合理的。反之，在同样条件下，如果P、O两点异侧布置，那么水平矛盾量将超过10mm，轮偏角可达4°。

由式（3-354）所计算的轮偏角，仅是转向机构一侧的车轮偏转角，为简化分析，此处就把它当作车轴偏离角。

车身在侧向加速度j的作用下，置于车身上的垂臂球头中心点O便绕侧倾力矩中心O₁转过一个θ角。同时通过横拉杆带动节臂球头点M横向移动了一个距离S。这个横向位移必然是通过节臂和车轮的偏转来实现的：

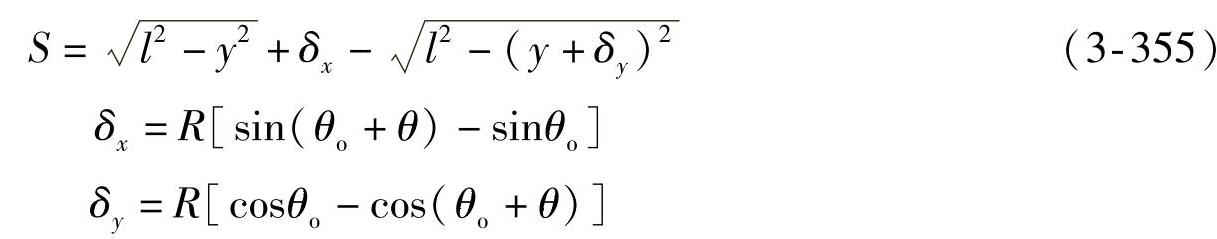
式中 l——横拉杆在横向平面上的长度（mm）；

x、y——垂臂球头中心点O的坐标（mm）；

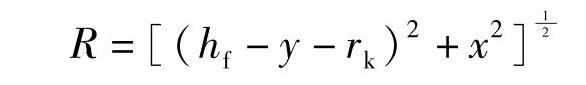
h_f——侧倾中心O₁距地面的高度（mm）；

r_k——车轮滚动半径（mm）；

θ_o——点O及点O₁的连线与纵向平面的夹角（°），θ_o=arcsin（x/R）；

θ——车身侧倾角（°）。

计算示例4

示例车型有关参数：l=900mm，x=150mm，y=40mm，h_f=550mm，r_k=365mm，节臂长r=145mm。

取侧向加速度j=0.4g时，侧倾角θ=3.5°。由式（3-355）可以计算下述参数：

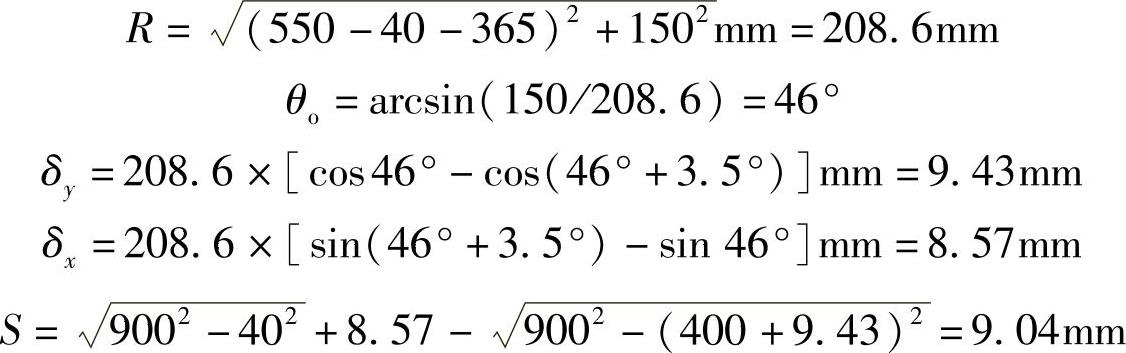
利用式（3-354）计算车轮偏转角为

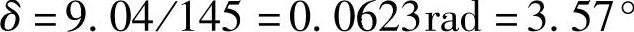
由图3-110的情况可知，所增σ角是与转弯方向一致的，故属过多转向趋势。

假如在其他条件相同的情况下，使侧倾中心O_l降低，便可减少车轮偏转角。若使点O₁低于垂臂球头中心O，那将使过多转向趋势变为不足转向趋势。