在空气弹簧的设计计算中，主要参数是有效面积A。如图3-88所示，空气弹簧上所受的载荷为

式中 R——空气簧的有效半径；

p——空气弹簧的内压力。

1.空气弹簧的垂直刚度

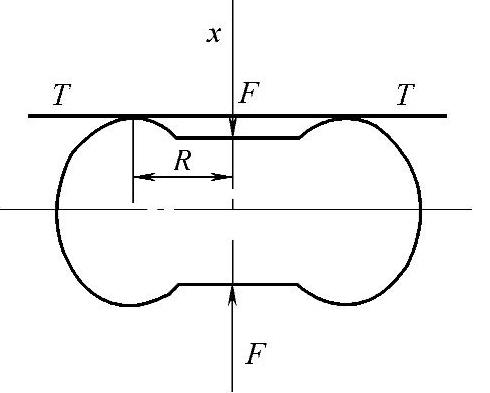
图3-88 有效面积的定义

空气弹簧在工作位置时，垂直刚度c的计算公式为

式中 p——空气弹簧的内压力；

p_a——大气压力；

V——空气弹簧的有效体积；

χ——多变指数，在等温过程（如计算静刚度时）χ=1，在动态绝热过程χ=1.4，在一般动态过程x=1.33～1.38。

从式（3-299）可以看出：

①空气弹簧的体积越大，其垂直刚度越低，所以连接附加空气室可以减小空气弹簧的垂直刚度。

②空气弹簧的垂直刚度和它在变形时有效面积的变化规律有关。如果dA/dx<0，即空气弹簧在压缩时其有效面积减小，则式（3-299）右边第二项为负值。也可用这个方法减小空气弹簧的垂直刚度。

计算空气弹簧垂直刚度的主要问题是确定与空气弹簧几何形状有关的dA/dx。

设dA/dx=aA，于是式（3-299）可改写为

式中 a——垂直特性形状系数。

表3-51列出了各种形式空气弹簧的垂直特性形状系数计算公式。

图3-89和图3-90是根据表3-51中的有关公式作出的空气弹簧垂直特性形状系数a的计算图。由这些图可以很方便地根据需要选择适当的几何参数，使形状系数a取得很小，以达到降低垂直刚度的目的。

表3-51 空气弹簧的垂直特性形状系数a

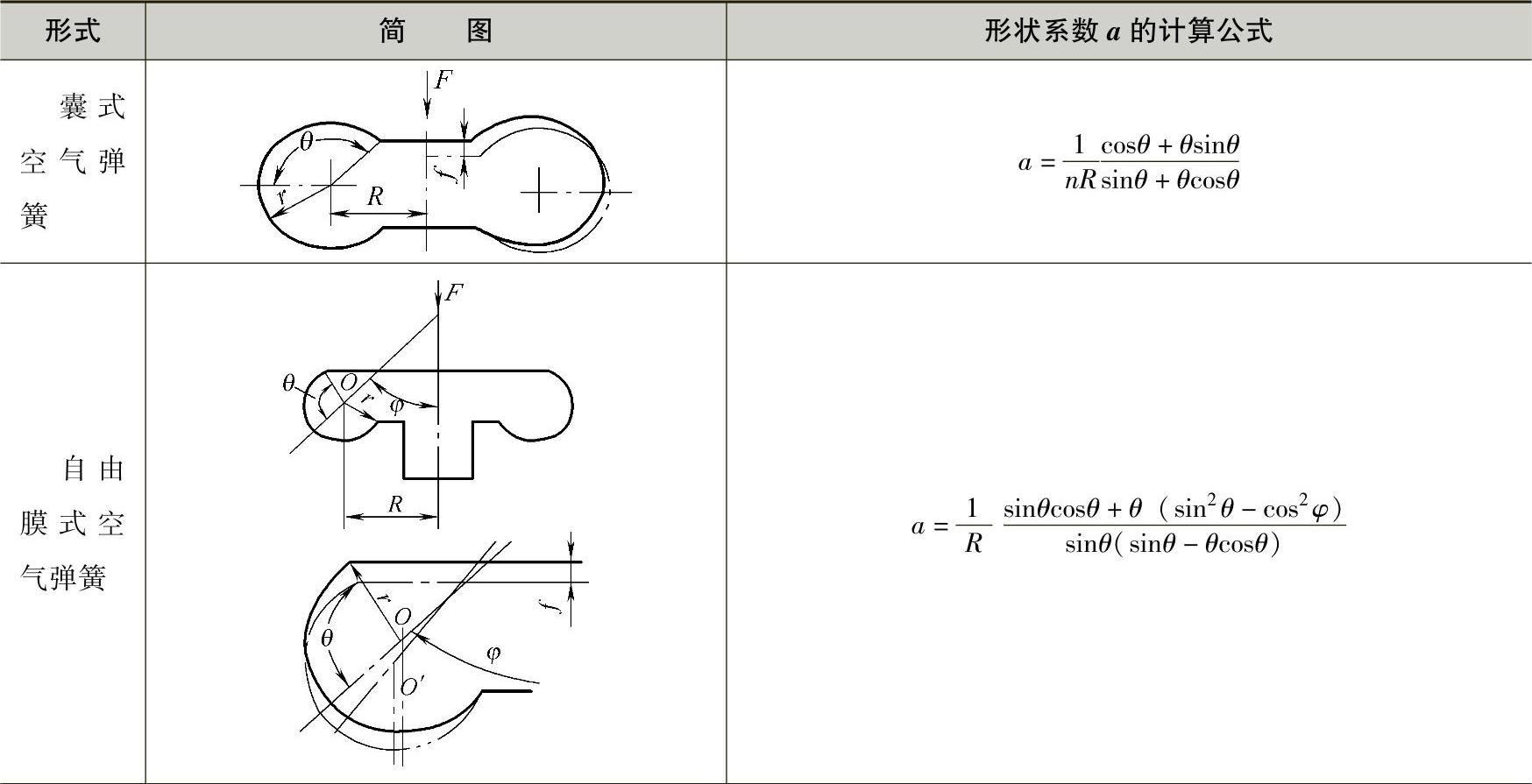
（续）

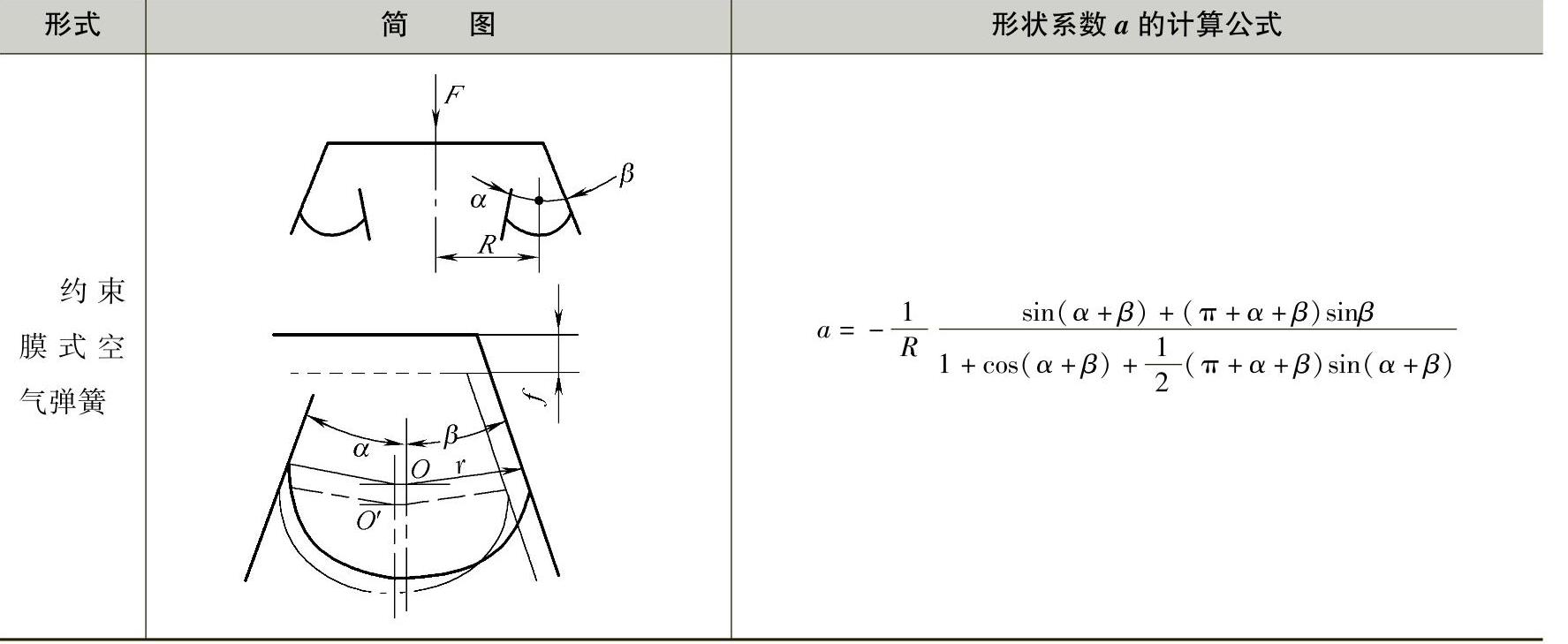
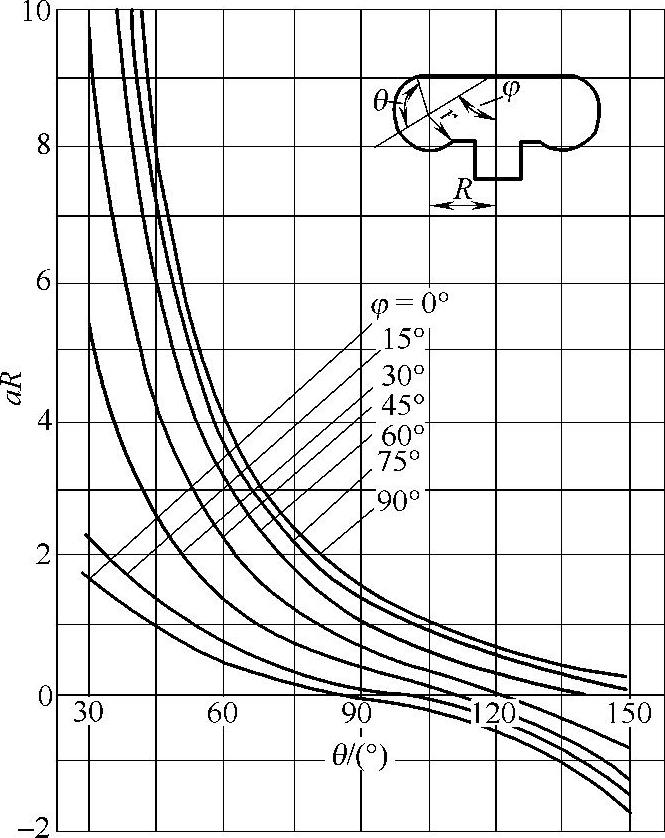
图3-89 自由膜式空气弹簧的形状系数a

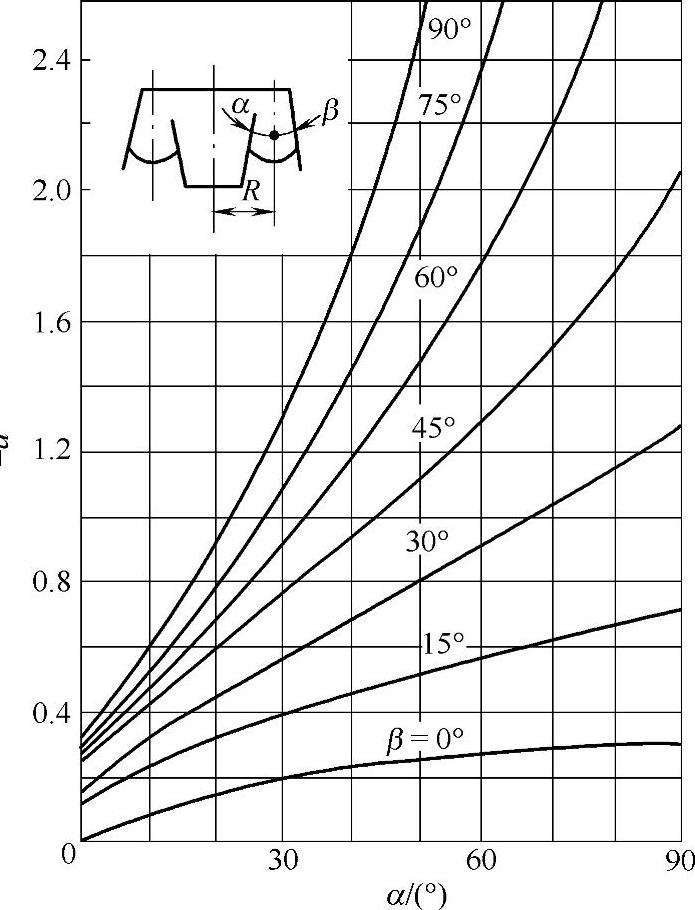
图3-90 约束膜式空气弹簧的形状系数a

2.空气弹簧的横向刚度

空气弹簧的横向刚度计算要比垂直刚度计算困难，因为它不仅与空气弹簧的几何形状有关，而且受材质的影响也较大。

（1）囊式空气弹簧

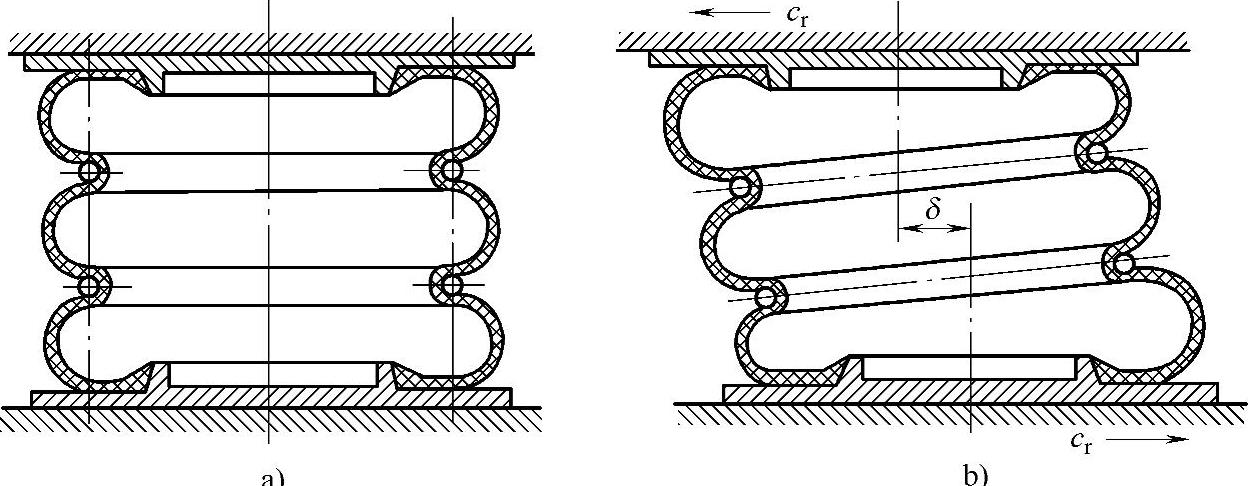
一般囊式空气弹簧在横向载荷作用下的变形，是受弯曲和剪切作用的合成变形。橡胶囊式空气弹簧在横向载荷作用下的变形如图3-91所示。

①单曲囊式空气弹簧的弯曲刚度（图3-92）计算公式为

式中 a——囊式空气弹簧的垂直特性形状系数，可由表3-51中的有关公式确定。

②单曲囊式空气弹簧的剪切刚度（图3-93）计算公式

(www.daowen.com)

图3-91 橡胶囊式空气弹簧在横向载荷作用下的变形

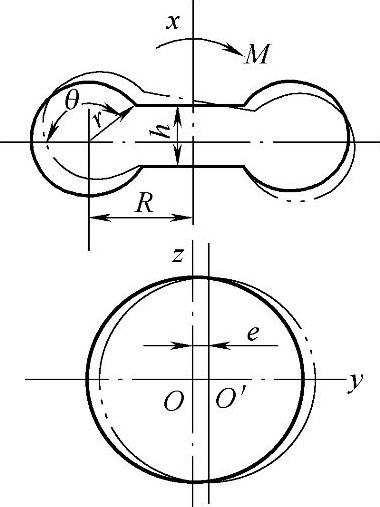
图3-92 空气弹簧的弯曲变形

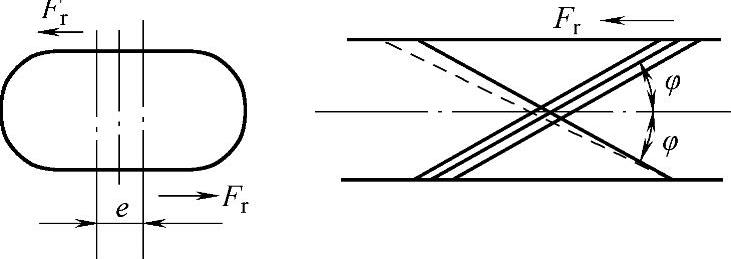
图3-93 空气弹簧的剪切变形

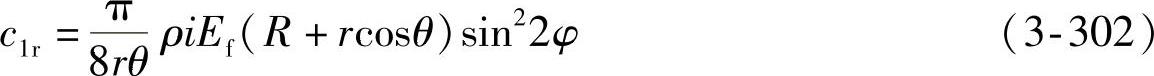
式中 ρ——帘线的密度；

i——帘线的层数；

E_f——一根帘线的截面积与其纵向弹性模量的积；

φ——帘线相对纬线的角度。

对于多曲囊式空气弹簧，横断面受弯曲和剪切载荷而发生的变形，可以利用力和力矩的平衡，将各曲的变形叠加起来而得到。若横断面总的变形很小，则多曲囊式空气弹簧的横向刚度c_r可由下式计算求得

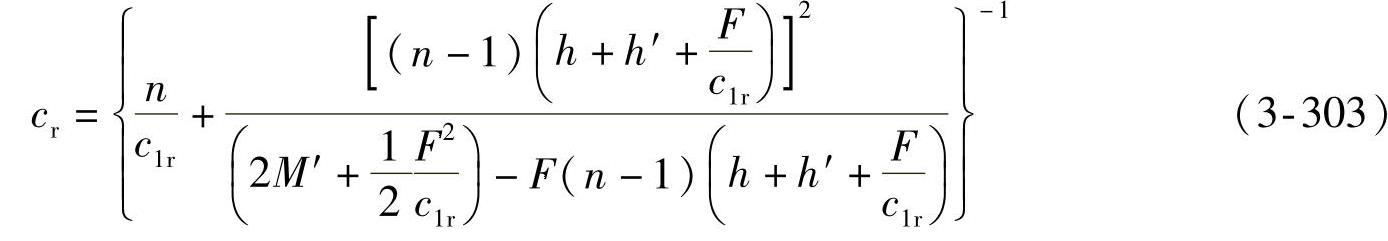
式中 h——一曲橡胶囊的高度；

h′——中间腰环的高度；

F——空气弹簧所受垂直载荷；

M′——弯曲刚度，由式（3-301）计算；

c_1r——剪切刚度，由式（3-302）计算；

n——空气弹簧的曲数。

由式（3-303）可以看出，空气弹簧的曲数越多，则其横向刚度越小。实际上四曲以上的空气弹簧，由于弹性不稳定现象，已不适于承受横向载荷的场合。此外，在利用空气弹簧横向弹性时，应使横向振幅最大不超过橡胶囊高度的20%，尽可能控制在10%以下。

（2）膜式空气弹簧

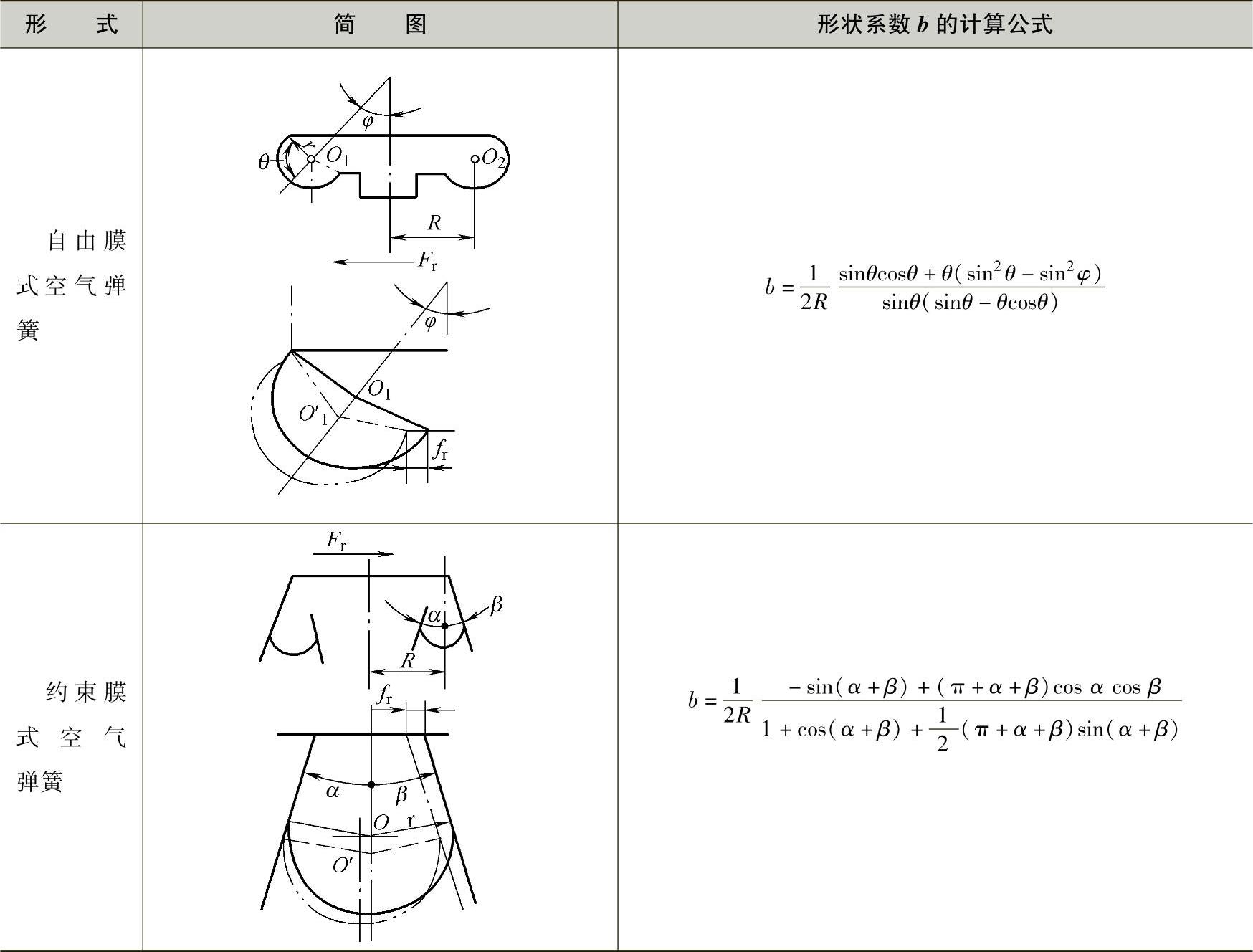
自由膜式和约束膜式空气弹簧的横向刚度c_r，可用如下公式计算

式中 p——空气弹簧的内压力；

A——空气弹簧的有效面积；

c₀——橡胶一帘线膜本身的横向刚度；

b——决定于空气弹簧几何参数的横向特性形状系数，其计算公式见表3-52。

图3-94和图3-95是根据表3-52中的有关公式作出的空气弹簧横向特性形状系数b的计算图。

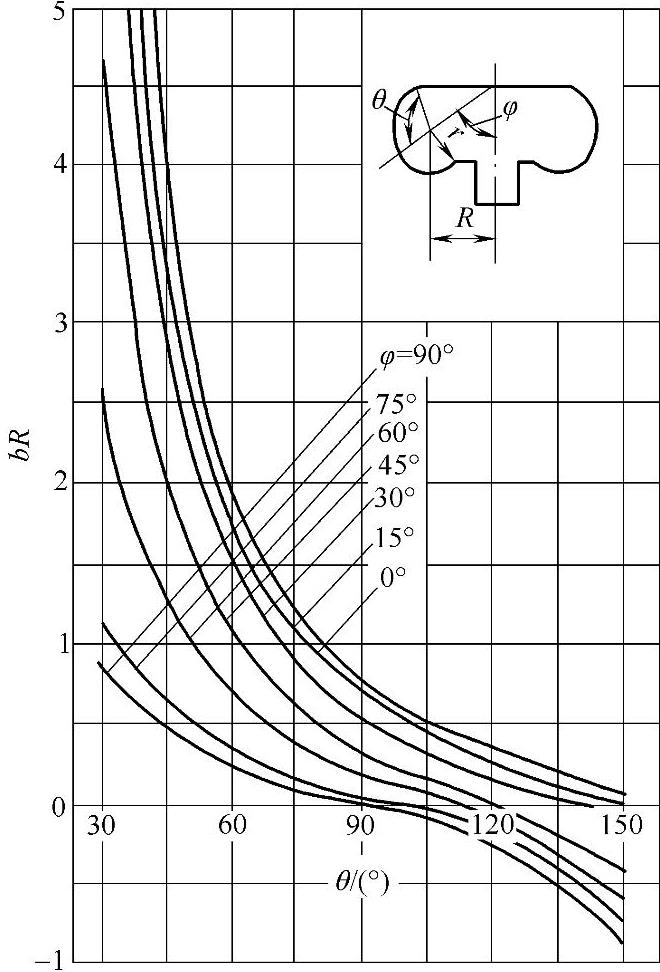
图3-94 自由膜式空气弹簧的形状系数b

（注：b为横向特性形状系数，R为气囊半径）

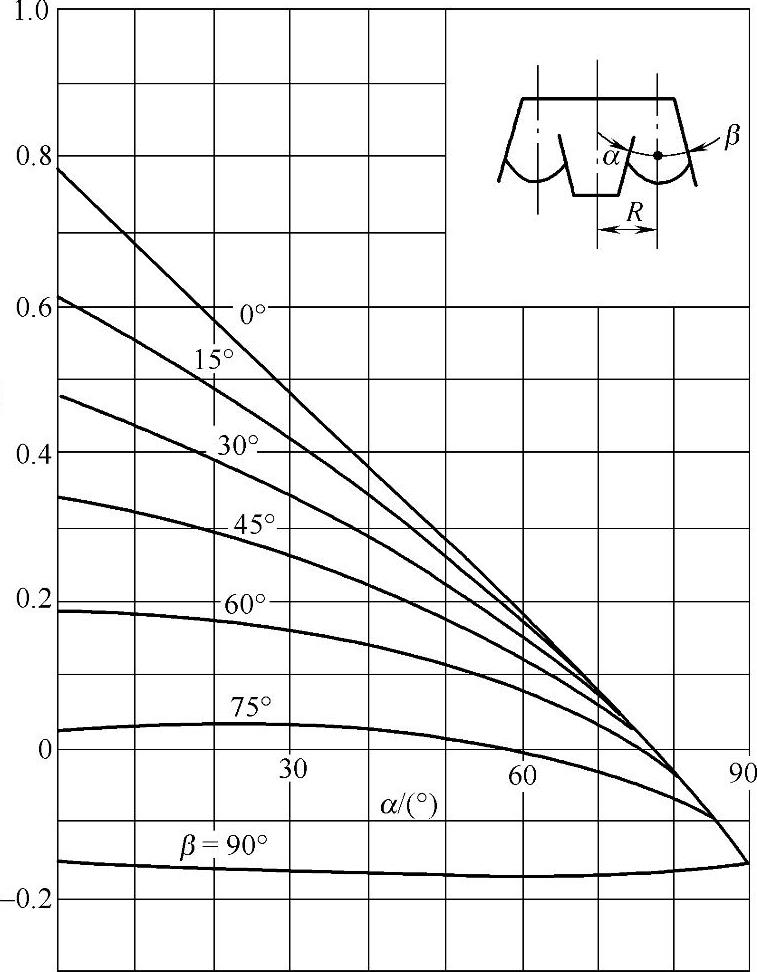
图3-95 自由膜式空气弹簧的形状系数b

（注：b为横向特性形状系数，R为气囊半径）

表3-52 空气弹簧的横向特性形状系数