等螺旋角圆锥压缩螺旋弹簧是变参数螺旋弹簧的一种，合理设计此类螺旋弹簧，不仅可以节约材料，降低重量，而且还可获得优良的工作特性，满足使用需要。

然而，由于此类螺旋弹簧较为复杂，加之诸多因素，故至今未见其可行的设计计算方法。本书拟在导出基本方程的前提下，建立负荷-变形特性等主要性能参数的计算方法。

1.基本方程

等螺旋角圆锥压缩螺旋弹簧钢丝中心线的展开线是一条直线，而它的顶视投影是一条对数螺旋线，如图3-70所示。

图3-70 等螺角圆锥压簧的几何特性

这种螺旋弹簧的簧圈半径R随极角θ变化的关系可描绘为

式中 R₀——有效簧圈首圈起始半径；

R_n——有效簧圈末圈终结半径；

n——弹簧有效圈数。

当用簧圈序号k（k=1，2，…，n）代替n后可得

当用R_k-1代替R₀后，又可得

然而，式（3-217）中的R_n和式（3-218）、式（3-219）中的R_k皆是一个未知数，故式（3-217）～式（3-219）均是一个待定方程，故须采用如下方法将其改造：

假设S_k为1～k个簧圈钢丝的投影长度，H_k为1～k个簧圈的弹簧高度，于是S_k和螺旋角α有如下关系：

而H_k和弹簧圆锥角ψ还有如下关系：

将式（3-221）代入式（3-220）后可得

S_k还可从另一角度求得。由图3-70可知

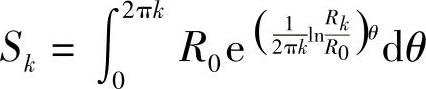
解此积分后便有

当令式（3-218）中的θ=2πk时，R=R_k，于是有

当令式（3-222）等于式（3-223），并代入式（3-224）后可得各簧圈半径与结构参数的关系式为

将式（3-225）代入式（3-218）后，便最终得到R与θ的以显式函数关系表达的基本方程为

2.负荷-变形特性

（1）轴向变形

当载荷F沿轴线方向作用于弹簧时，弹簧钢丝的截面受到力矩T_t、弯矩M_b、法向力F_t和径向力F_b的同时作用。然而，M_b、F_t和F_b对轴向变形都影响不大，故在推求轴向变形公式时，只考虑力矩T_t的作用。在忽略螺旋角影响的前提下，力矩T_t=FR，如图3-71所示。

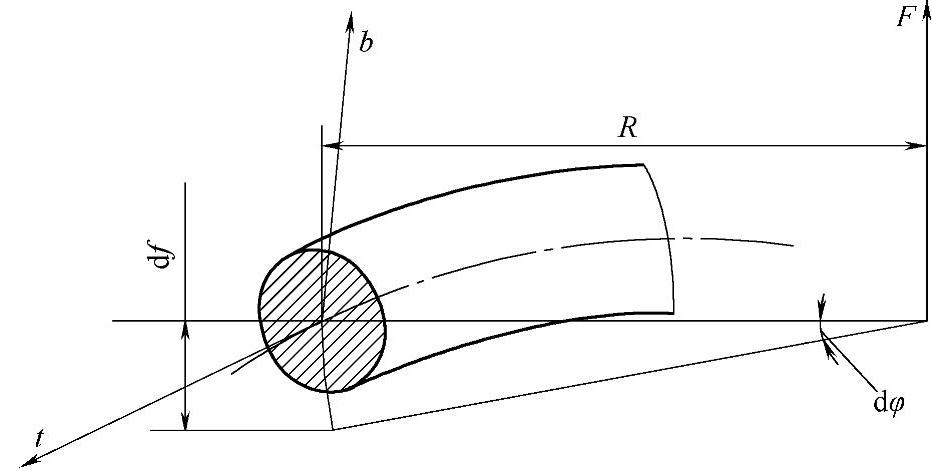
图3-71 钢丝在力矩T_t作用下的变形

从基本的扭转变形出发，利用式（3-226），便可求得弹簧第k个单圈的轴向变形，即

式中 dφ——钢丝在力矩T_t作用下的微元角位移，其计算公式为

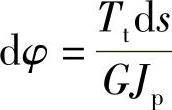
式中 J_p——钢丝的极惯性矩，圆形截面的极惯性矩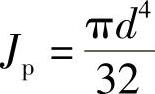：（d为钢丝直径）。

G——材料的抗扭模量；

ds——钢丝的微元长度，其计算公式为

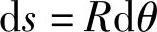
式中 dθ——极角的微元位移；

代入各参数后，积分变为

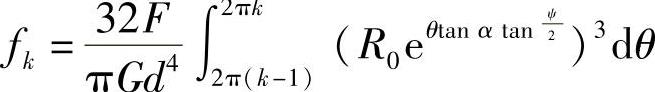
解此积分，可得第k个单圈的压并变形量为

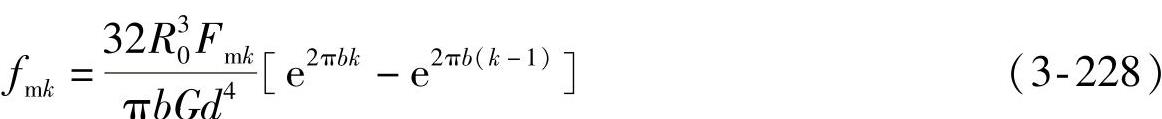
式中 b=3tanαtan（ψ/2）；

F_mk——第k个单圈的压并载荷（N）。

式（3-228）还可变为另一种形式为

式中

（2）第k单圈的压并载荷

变形是随载荷的增大而增大的，多大的载荷才能使第k个单圈压并呢？这是把握弹簧负荷-变形-特性必须要知道的。要知道第k个单圈的压并载荷F_mk，得先求出第k单圈的节距t_k和最大变形量f_mk。

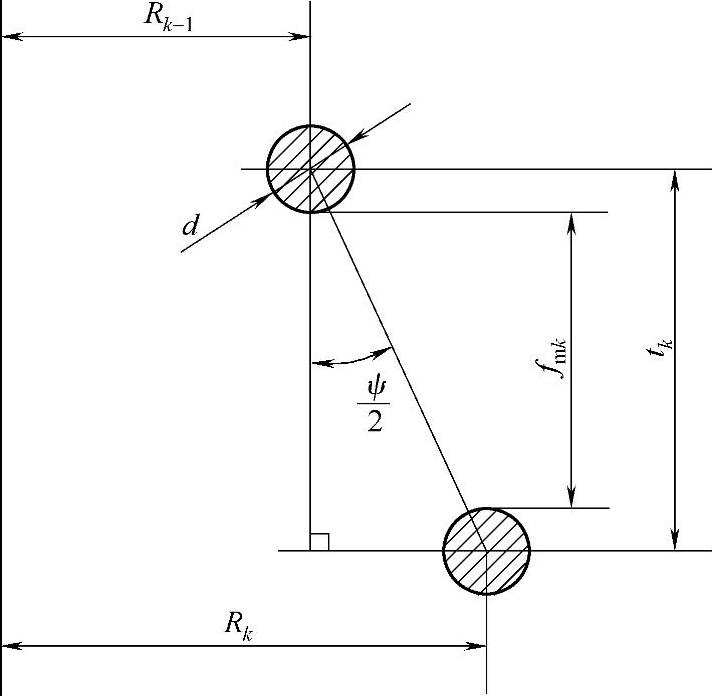
图3-72 第k圈的最大变形量

由图3-72可知，第k圈的节距为

第k圈压并时的变形量，也就是该圈的最大变形量，在ψ不是很大的情况下，可表示为

将式（3-231）中的f_mk代替式（3-229）中的f_k后，可解得

（3）全簧变形及刚度

当第k圈压并时，全簧的变形为(www.daowen.com)

当第k圈压并时，全簧的刚度为

3.相关参数

（1）有效钢丝投影总长度

令式（3-222）中的R_k=R_n，可得到弹簧有效圈数钢丝的投影总长度S_n为

（2）有效钢丝总长度

弹簧有效圈数钢丝的总长度L_n可表示为

（3）弹簧高度

弹簧有效圈数的总高度为

（4）弹簧质量

弹簧有效圈数的总质量为

式中 ρ——材料密度（g/cm³）。

（5）弹簧应力

当弹簧节距不是很大时，钢丝断面的受力状况如图3-73所示。

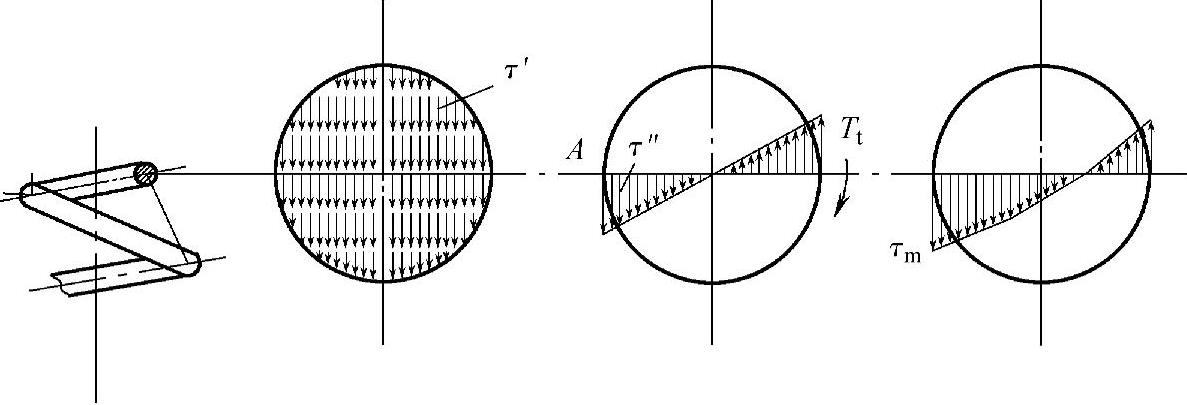
图3-73 钢丝断面承受的剪应力

力F_mk对钢丝截面的剪切作用引起第k圈的剪应力τ_k′，其方向与力F_mk相反，大小均布，数值为

力矩T_t使钢丝扭转，在与R所对应的截面上引起第k圈的剪应力τ″_k，其最大值发生在该截面的周边，其数值为

两项应力之和，即为该截面之最大总应力，它发生在断面内侧点A（危险点）。由于钢丝卷绕的曲率变化还将影响应力，需修正。修正后的最大剪应力为

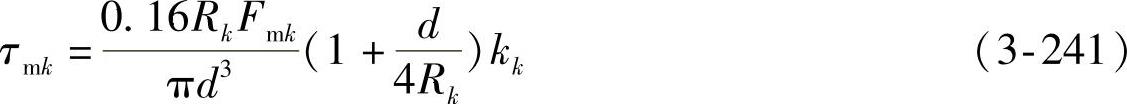
式中 k_k——修正系数（曲度系数），；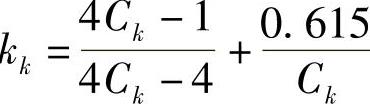

C_k——旋绕比，C_k=2R_k/d。

注意：弯曲应力σ约为剪应力τ的1.25倍。

4.螺旋角与圆锥角的影响

众所周知，螺旋弹簧的刚度与钢丝直径d的4次方成正比，与有效圈数n的1次方和簧圈半径R₀的3次方成反比，然而，当d、n和R₀均确定之后，作为圆锥簧的螺旋角α和圆锥角ψ又是如何影响弹簧性能的呢？

（1）α和ψ的影响

参数相同的两副圆锥螺旋弹簧，α和ψ大者，将产生如下效果：

①半径R_k增大，弹簧横向尺寸增加。

②节距t_k增加，弹簧高度增加。

③由于纵、横向尺寸增加，弹簧质量M增大。

④弹簧的刚度降低，变形量增大，频率降低。

⑤对于压并载荷，α增大，F_mk亦增大；而ψ虽增大，F_mk却降低。

⑥对于剪应力，α增大，τ_mk值和首、末圈应力比τ_m1/τ_mn均增大；ψ增大，τ_m1/τ_mn也增大，但τ_mk值却降低。

（2）无簧圈叠压圆锥簧的ψ值

圆锥角ψ增大，不仅产生上述效果，且圈间挤压力和径向力均增大，甚至有可能自锁而不回弹。当ψ值增大到（R_n-R₀）≥nd时，所有簧圈均落在支座上。此时的圆锥簧便成了无簧圈叠压的圆锥簧，其压并高度H=d。这种螺旋弹簧的优点是在空间高度受限制时，在不影响总变形量的情况下，可降低弹簧的高度。然而，它的底圈尺寸过大，没有足够的横向尺寸是不能采用的。

在设计无簧圈叠压的等螺旋角圆锥簧时，在R₀、n、α和d已定的情况下，圆锥角ψ可按下述方法求得。

由图3-74可知，等丝径圆锥簧有如下关系：

式中 δ——给定的压并后各圈钢丝的平均间隙。

又由式（3-225）可知，等螺角圆锥簧有如下关系：

令式（3-242）等于式（3-243），可解得

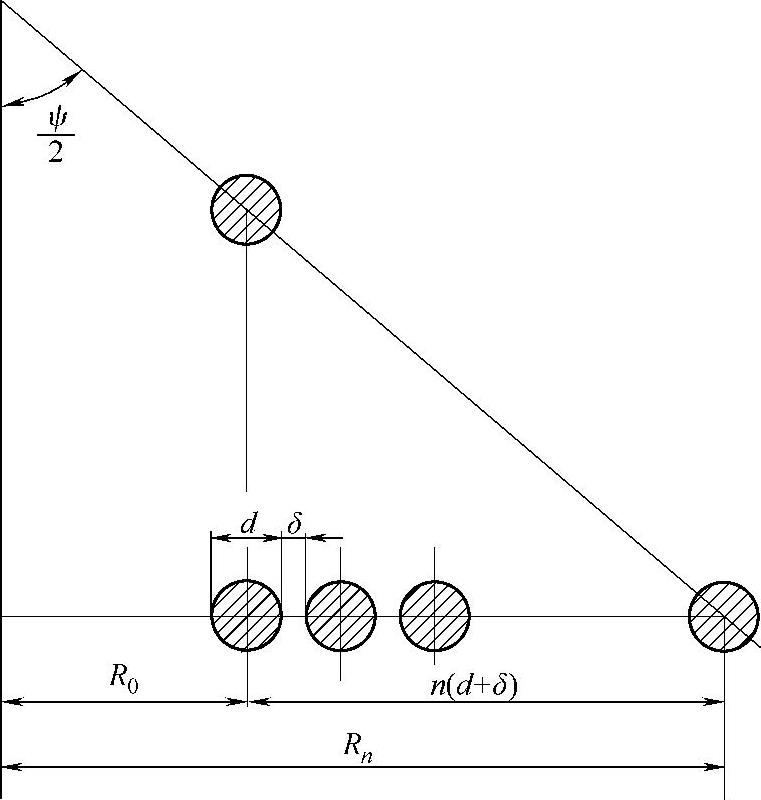
图3-74 无簧圈叠压圆锥簧的ψ值

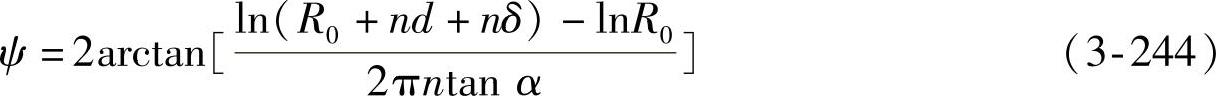
5.计算示例及计算步骤

参数：直径d=3cm，初始圈径R₀=8cm，圆锥角ψ=10°，螺旋角α=6°，有效圈数n=7。

用式（3-225）、式（3-229）、式（3-230）、式（3-232）、式（3-233）、式（3-234）、式（3-236）、式（3-237）、式（3-238）、式（3-242）分别求得R_k、η_k、t_k、F_mk、f_gk、c_gk、τ_mk、L_n、H、M，其计算结果见表3-48，特性曲线如图3-75所示。

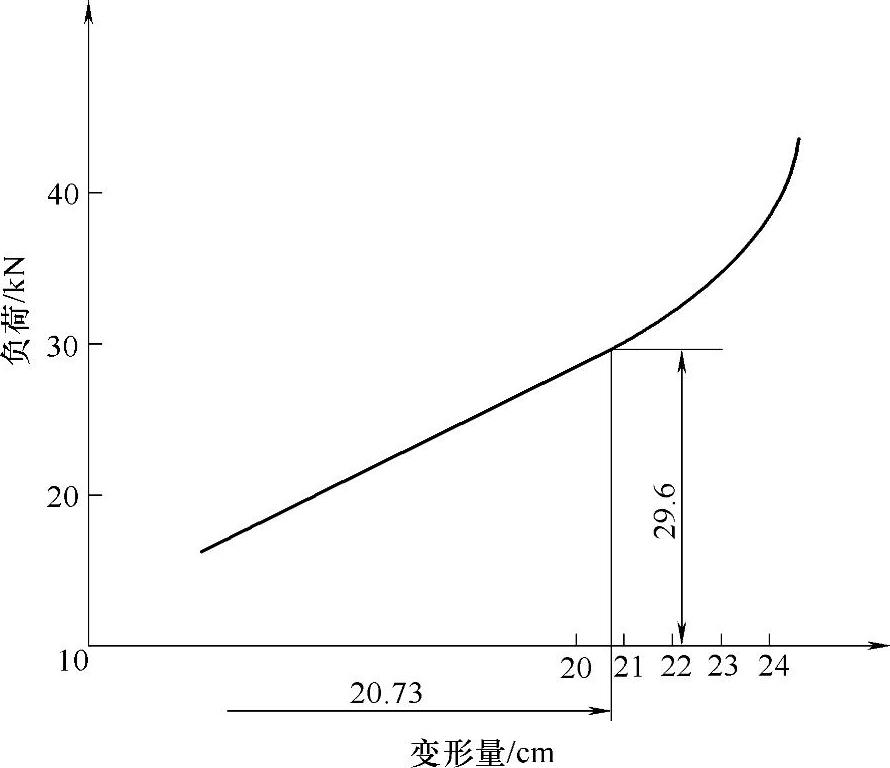
图3-75 负荷-变形特性

表3-48 主要参数的计算结果

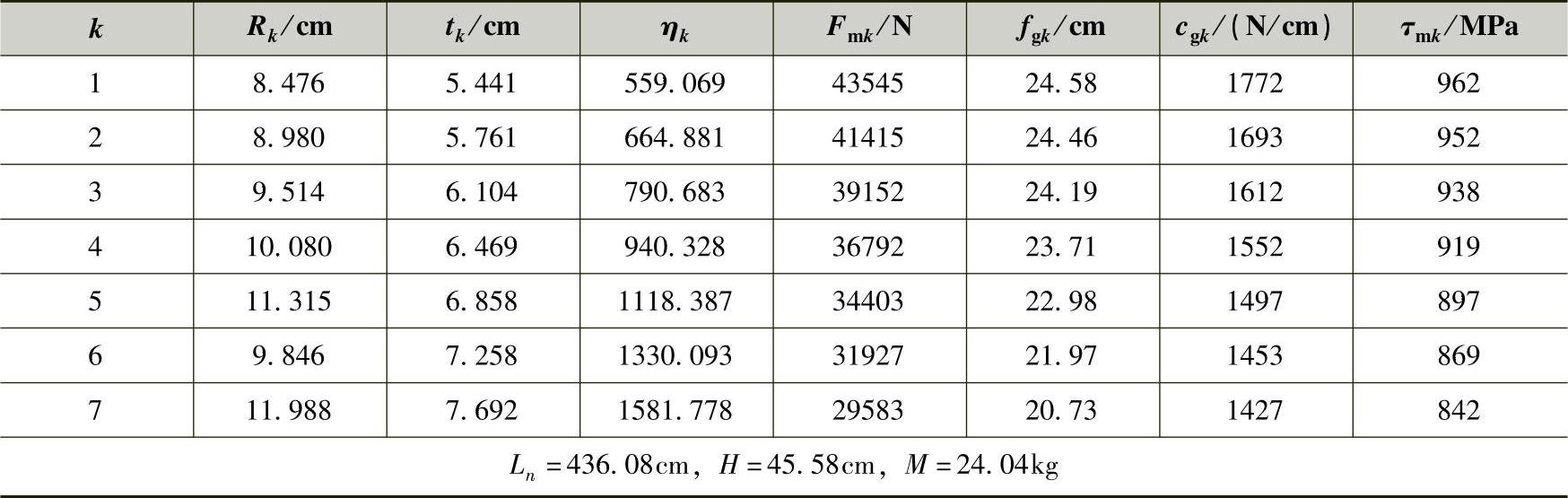
从表3-48数据可知，当载荷从29.6kN增至43.6kN时，刚度c_gk从1427N/cm达到了1772N/cm，增幅约为24.18%，这说明示例弹簧的载荷特性还是较好的。

6.结论

①导出的R与θ关系的基本方程式（3-226），为等螺旋角圆锥压簧计算方法的建立奠定了基础。

②建立的计算方法，为等螺角圆锥压簧的设计提供了可行的依据。

③为提高整簧的刚度变化幅度和压并载荷，充分发挥材料的潜能，此类弹簧应与变丝径簧结合设计。

④为节约材料和避免底圈尺寸过大，此类螺旋弹簧宜设计成中大两端小的双锥型“”或中间直两端小的桶型“”。