变圈径等节距压缩螺旋弹簧也就是圆锥压缩螺旋弹簧，它也是一种变刚度簧，参见图3-68。这种螺旋弹簧受载后，起初保持线性特性；当载荷逐步增大时，弹簧从最大圈开始逐渐并紧，直至所有圈全部并紧。大圈一开始并紧，弹簧便进入非线性特性。

Ψ是圆锥簧的锥角，其数值越大，弹簧刚度的变化就越大，就越能适应汽车负荷的变化，消除或缓和共振。然而，圈间压并后，挤压力和径向力均增大，且有可能发生自锁而不回弹。当Ψ值大到弹簧小端半径R₀与大端半径R_m构成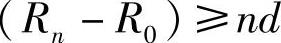时，所有圈均落在支座上，其压并高度H_b=d。

圆锥螺旋弹簧分等节距和等螺旋角两种，下面先研究等节距螺旋弹簧的变形公式。

1.螺旋弹簧的变形

等节距等丝径变圈径螺旋弹簧，其钢丝中心线的展开线是一条上凸曲线，钢丝中心线在xy平面上的投影为阿基米德螺线，如图3-69所示。

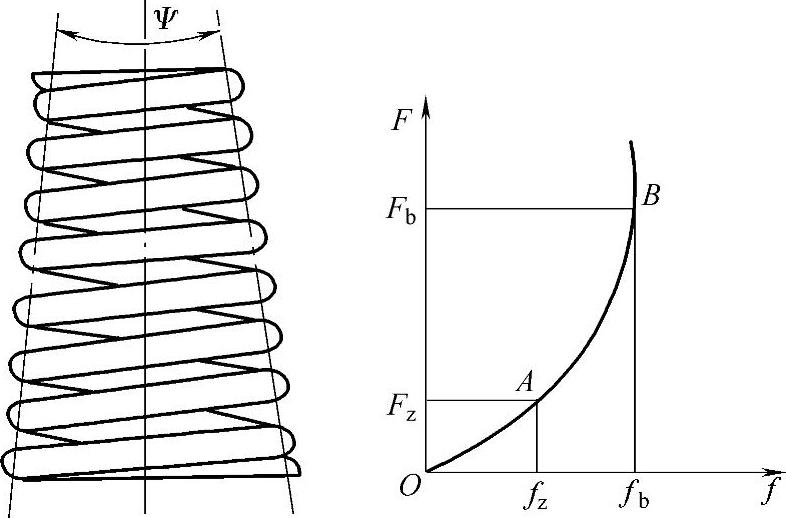
图3-68 变圈径螺旋弹簧

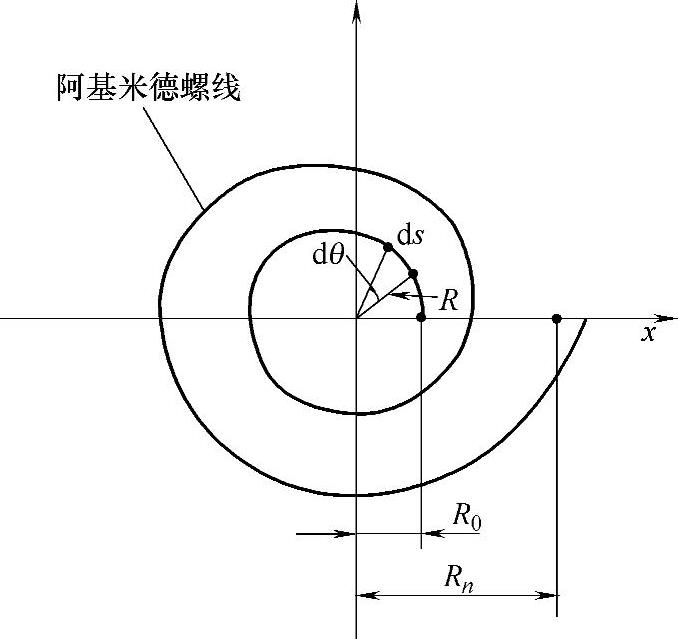
图3-69 钢丝中心线的投影

阿基米德螺线随着极角θ的变化，曲率半径R也随之变化。因此，作用于螺旋弹簧的力F所构成的扭矩是随极角变化的。所以要求弹簧的变形，就必须求出半径R随θ的变化关系。

由图3-69可知，当θ增加2π时，半径增加量为

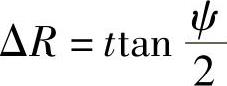
式中 t——节距；

ψ——螺旋弹簧圆锥角。

即随θ变化的半径为

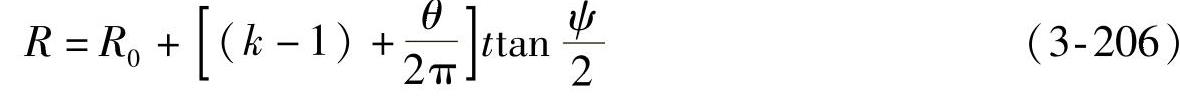
第k圈钢丝在水平面上的投影长度S_k为

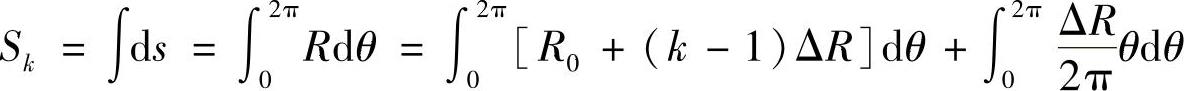
于是有

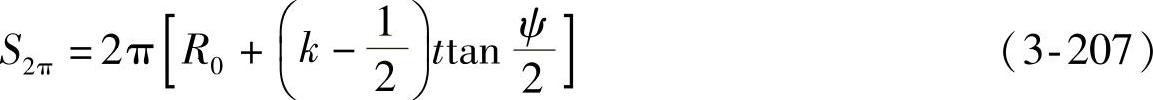
投影长度随极角变化的关系式为

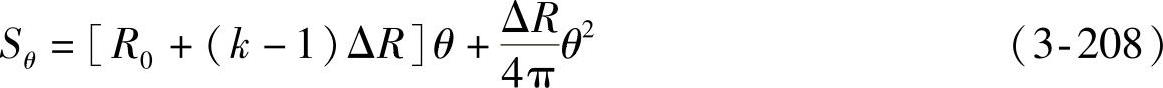
半径随θ变化的关系式为

式中

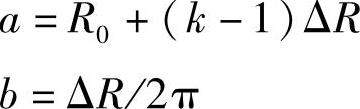
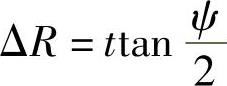
下面推求第k圈的变形量f_k

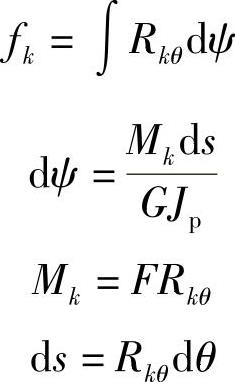(www.daowen.com)

代入上式可得

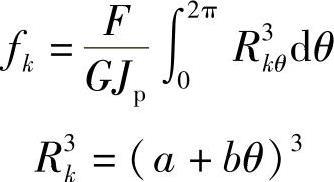
于是有

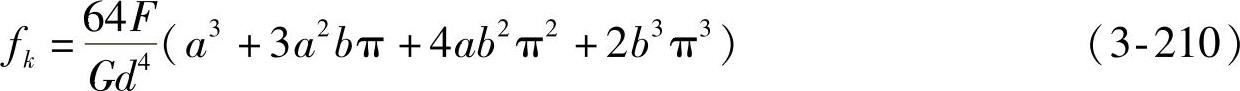
式中，k=1，2，3，…，n。

整根螺旋弹簧的变形量为

2.变形公式的另一种推法

极角每增加2π时，半径增加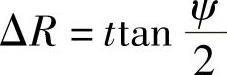，因而任意点的半径为

当θ=2πn时，R=R_n（末圈半径）。

由此可得

将式（3-213）代入式（3-212），可得任意极角的半径为

下面对变形公式的推导进行说明。

根据莫尔定理有

式中 T_t——绕钢丝截面中心线切线的扭矩，T=FR；

T₀——单位扭矩，T₀=1×R=R；

ds——钢丝微元长度，。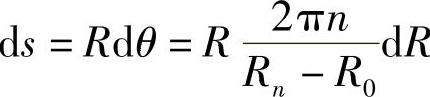

将各式代入式（3-215），并将积分限改为R₀到R_n，则可得整簧的变形量为

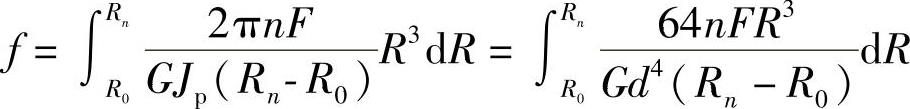
即

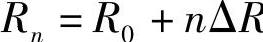
式中

式（3-210）和式（3-216）计算结果完全一致。计算示例参见附表3。