变参数压缩螺旋弹簧（以下简称螺旋弹簧），由于其独特的非线性性能，故在各种机械设备和仪表器具等方面有着广泛的应用。特别是在那些高性能汽车的悬架上，更是受到青睐。如德军曼（MAN）280的10t重型越野车、美军高机动多用途轮式车（HM-MWV）系列车型等均采用了变参数螺旋弹簧。

什么是变参数螺旋弹簧呢？众所周知，钢丝直径d、簧圈中径D（以下简称圈径）、节距t、螺旋角α，这是螺簧的四大结构参数。这四大结构参数全部保持不变者，则是普通圆柱螺旋弹簧；这四大参数之一、之二、之三或全部随钢丝长度L变化者，则称为变参数螺旋弹簧。

变参数螺旋弹簧不仅计算方法有待建立和完善，而且其主要性能也需探索了解。为更好地指导变参数螺旋弹簧的设计，本书在对其进行科学分类之后，研究了参数变化对其主要性能的影响，阐明了固有的优缺点，并提出了性能评价指标。特别是对各种典型的变参数螺旋弹簧建立了实用的计算方法，并对其主要性能作了对比计算（计算方法的建立过程以及对比计算过程从略），计算条件和计算结果均以表格的形式列出。在上述工作的基础上，对其进行了全面的归纳分析，并做出了可用于指导设计的结论性评价。

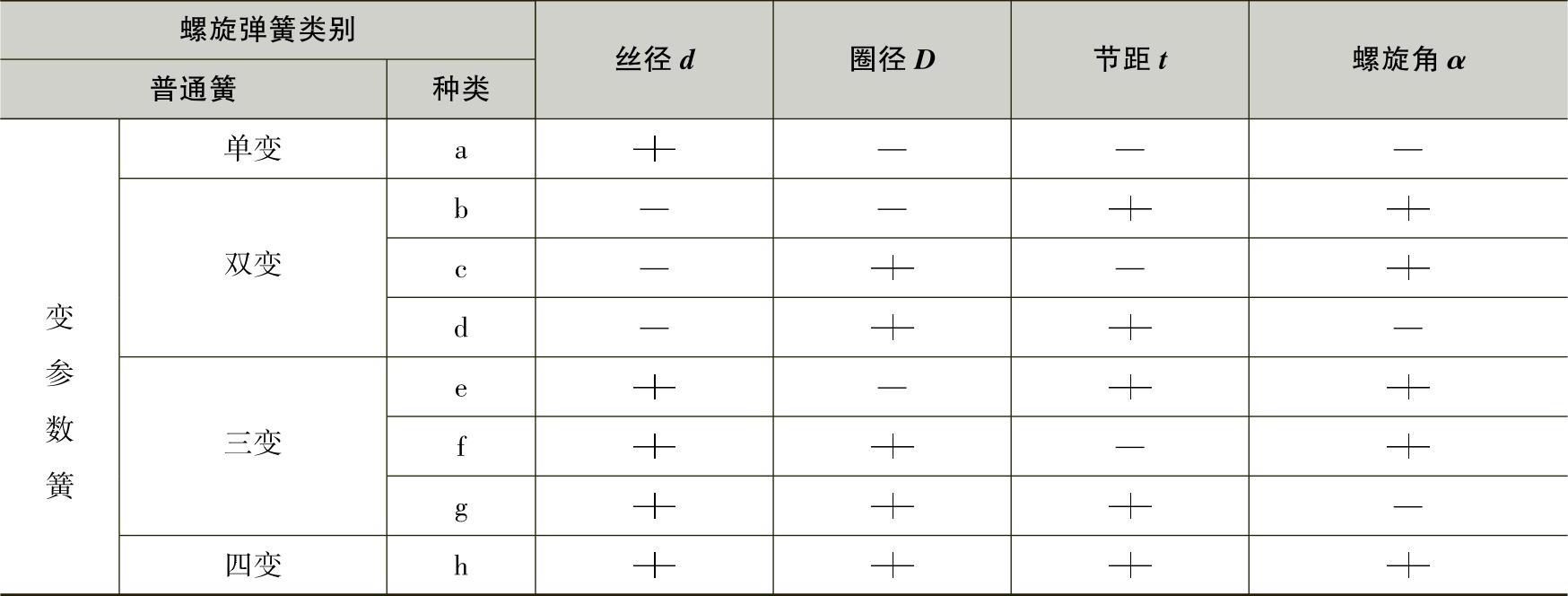
1.分类

普通螺旋弹簧，是一种最为简单的圆柱螺旋弹簧。而变参数螺旋弹簧，则可根据结构特点分为元件（零件）和组件（部件）两个种别。所谓元件，就是单纯的圆柱簧或圆锥簧。所谓组件，则是由圆柱螺旋弹簧和圆锥螺旋弹簧组合而成的复合螺旋弹簧。由于参数变化的不同和组合方式的不同，它们还各自分为若干类型。

（1）元件的分类

元件分类主要是如下三种变化的组合结果：

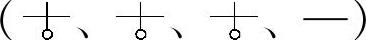一是四大基本参数（d、D、t、α）的变与不变。变则采用“”表示，不变则采用“—”表示，例如：类别代号，便是变丝径、变圈径、变节距、等螺角的圆锥螺旋弹簧。

二是当给定每一基本参数的初始值后，按簧圈序号从上往下数按k=1，2，…，n的顺序，若参数是从小变到大，则采用符号“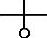”表示；若参数是从大变到小，则采用符号“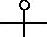”表示。例如，类别代号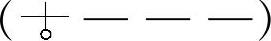便是丝径从小变到大，圈径、节距、螺角皆不变的圆柱簧。

三是每一参数变化速率的大小，如对变丝径簧，钢丝锥角β值的取大取小，再如圆锥簧锥角ψ值的取大取小等。

此外，尚有一些特殊类型的螺旋弹簧，如变丝径、等内径螺旋弹簧等，其圈径随簧高的变化呈一条指数曲线，这是一类很有实用价值的螺旋弹簧。

上述种种变化的组合，可以得到数十种元件簧，故不可能将其一一列出，现仅将因四大参数的变与不变所组合得到的8种元件螺旋弹簧列于表3-44中。

表3-44 变参数螺旋弹簧（元件）四参数变化分类

（2）组件的分类

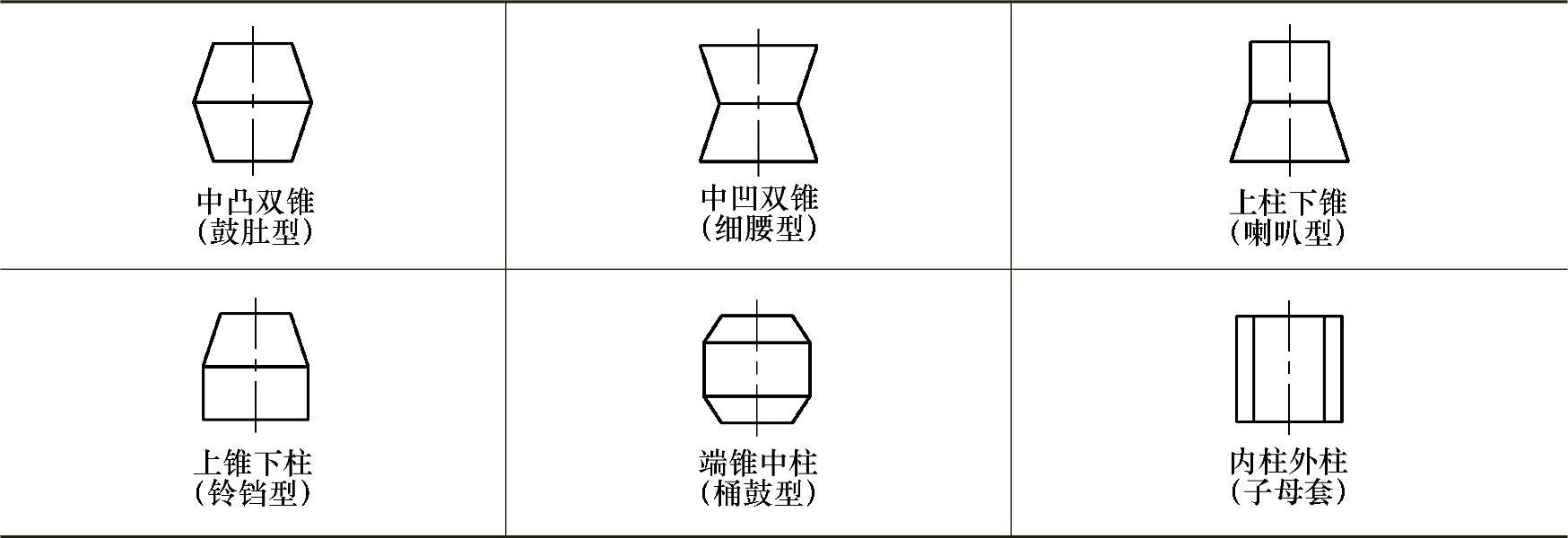
变参数组件螺旋弹簧是由变参数元件螺旋弹簧按不同方式组配而成，因此其品种类型较元件更为繁多。表3-45所列6类典型组件，仅是锥簧与柱簧的简单搭配，至于丝径、圈径、节距、螺旋角是否变化以及变化速率如何，此处一律不涉及。

表3-45 6类典型的变参数组件螺旋弹簧

2.主要性能

变参数螺旋弹簧的核心在于一个“变”字。通过结构参数等的不同变化，以获得优良的载荷-变形特性和满意的应力分布特性。那么结构参数等的变化又是如何影响载荷特性和应力特性的呢？

（1）载荷-变形特性

若设螺旋弹簧中心O为坐标原点，θ为极角，S为钢丝展开线的投影长度，并假定在螺旋角α不大于9°的情况下，忽略弯曲和纯剪引起的微小变形，那么圆形断面钢丝螺旋弹簧的刚度c与簧圈半径r和钢丝直径d的关系可表示为

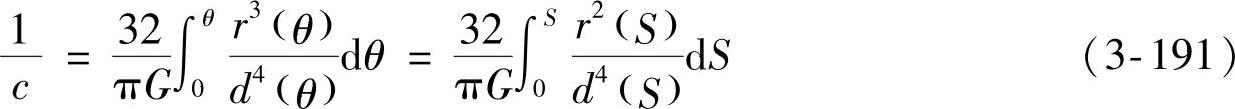
由式（3-191）可知螺旋弹簧在设计上大有文章可作：因为r和d可随θ或S变化，所以，只要调整圆锥角ψ的数值，便可获得r随θ或S变化的不同函数；只要改变钢丝锥角β的值，便可获得d随θ或S变化的不同函数，从而获得所期望的c随θ或S变化的函数。

然而，一个螺旋弹簧的圈径函数r（S）和丝径函数d（S）一经确定，那么这个螺旋弹簧的刚度c就被基本确定。此时，要改变刚度的唯一可能，就是改变弹簧钢丝的有效长度或有效体积。改变螺旋弹簧钢丝的有效长度或有效体积的措施就是减少有效圈数。而减少有效圈数又是通过改变载荷函数来实现的。

由于圈径函数r（S）和丝径函数d（S）的变化，各个簧圈的刚度是不同的，不同刚度簧圈的压并载荷F_k也是不一样的。因为各个簧圈的节距t的不同，所以压并不同节距簧圈的载荷也不相同；不同的螺旋角α将造成不同节距t的簧圈，故各簧圈压并载荷也不相同。所以，变节距簧或变螺旋角簧也是改变钢丝有效长度和有效体积的措施之一。

螺旋弹簧在工作时，随着载荷F的逐渐增加，变形f也逐渐增加。当载荷F增加到一定程度的F_fm时，刚度最低或节距最小的簧圈将首先被压并。在首个簧圈的压并过程中，由于圈间钢丝并非逐点连续接触，弹簧仅按着一定的斜率保持着线性关系变化。随着载荷的继续增加，余下的簧圈将按由弱到强的顺序依次逐一被压并，直至整簧被压并。此时的压并载荷F_em既是末圈的压并载荷，也是全簧的压并载荷，此时的压并变形就是全簧的最大变形f_em。

螺旋弹簧每压并一圈，刚度便提高一步，刚度曲线的斜率便增大一步。所以，一般来说，实用的变参数螺旋弹簧的负荷-变形特性是一条阶跃式的折线，如图3-63所示。

（2）应力特性为方便分析，先列出较为典型的分类结构代号为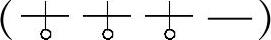的变参数螺旋弹簧第k圈的最大剪应力表达式：

式中 k_k——第k圈的修正系数；

F_km——第k圈的压并载荷（N）；d_k——第k圈终结点的丝径（cm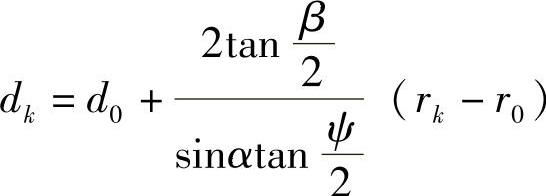），，其中d₀为钢丝的初始直径（cm），r₀为簧圈的初始直径（cm）；r_k——第k圈终结点的簧圈半径（cm），

由式（3-192）可知，变参数螺旋弹簧第k单圈的最大剪应力τ_km，除与该圈的压并载荷F_km有关外，还与该圈终结点的簧圈半径r_k的一次方成正比，与该圈终结点的丝径d_k的三次方成反比。深入一层看，r_k和d_k除和d₀、r₀、α、β和ψ五大结构参数有关外，它们还是序号k和钢丝长度L的函数。设计时，改变结构参数，便能改变各圈的压并应力。当把τ_km随F_km变化的数值进行归纳后，便可得到图3-64所示的斜率逐步降低的一条上凸曲线。

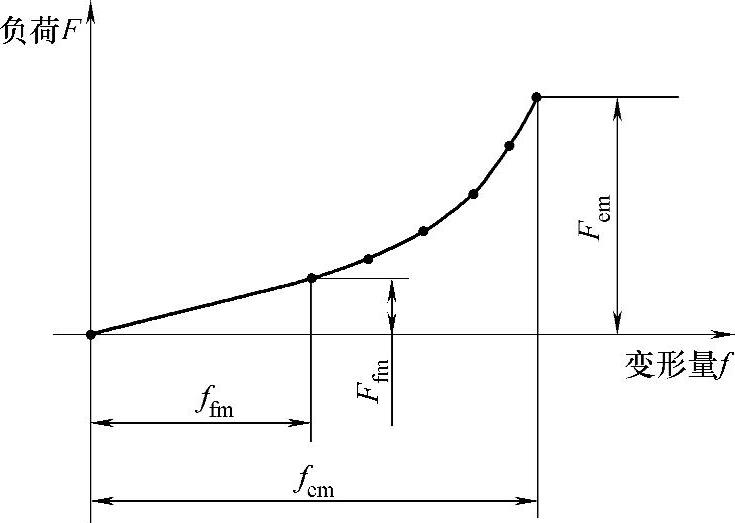
图3-63 变参数螺旋弹簧的负荷-变形特性

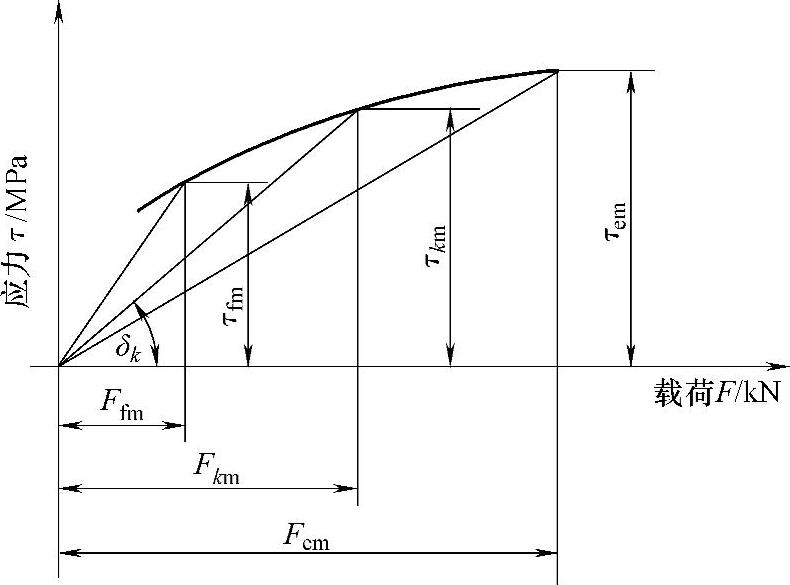
图3-64 典型变参数螺旋弹簧的载荷应力特性

普通螺旋弹簧是由结构参数完全相同的n个单圈组合而成的，故各圈的压并载荷F_km和压并应力τ_km均相等，其应力分布也是完全均匀的。

变参数螺旋弹簧是由结构参数不同的n个单圈组合而成的，故图3-64中的F_km和τ_km均不相等，应力分布也不均匀。

应力似乎越低越好，其分布似乎越均匀越好，对于变参数螺旋弹簧，这既做不到，也无必要。首先，应力不是越低越好，而是在许用应力容许的范围内越高越好，因为这样才能充分发挥材料的潜能。须知，零应力就是不让材料参与工作，充分负载正是变参数簧的优势！其次，应力分布的均匀性是结构参数一致性的反应，片面地追求均匀性，无异于放弃变参数螺旋弹簧的变化性和合理性。

设计者的任务在于利用结构参数的可变性，在满足优良的载荷变形特性的前提下，实现应力的合理分布。

在图3-64中，各圈压并应力τ_km和各圈的压并载荷F_km的比值，代表着应力随载荷变化的变化率。此处还将其命名为各圈的比应力R_kτ（MPa/kN），即

R_kτ的力学概念是单位载荷下的应力。因此，希望R_kτ值越低越好。

普通螺旋弹簧的比应力是一个常数，即R_kτ=C。然而，变参数螺旋弹簧的R_kτ值，一般来说则是随簧圈序号k变化的，也就是当钢丝长度L变化时，应力随载荷发生或大或小的变化。到底是逐步变大还是逐步变小，或是先变大再变小，这是由各圈结构参数决定的。

变参数螺旋弹簧R_kτ值的变化，粗略地遵循如下规律：各圈比应力R_kτ值之积的均方根值趋于一个常数，即

这个常数C，就是全簧有效总质量M、圈数n和全簧总变形f_g等参数与之大致相等的普通螺旋弹簧的R_kτ值。

在式（3-194）的前提下，压并末圈的比应力R_kτ值越小越好。因此此时的压并载荷是全簧的最大压并载荷F_em，R_kτ值小，τ_em值就相对减小，这正是变参数螺旋弹簧应力分布合理性的体现，也是合理用材的体现。

图3-64所示为典型变参数螺旋弹簧的应力分布规律：应力随载荷增大而增大，比应力随载荷的增大而减小。然而，还有不少变参数螺旋弹簧，应力分布更为特殊：在低载荷区段，应力随载荷的增大而增大，而在高载荷区段应力则随载荷的增大而减小；高载荷区段的比应力变得更小。例如，分类结构代号为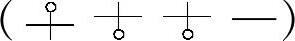和的变参数螺旋弹簧，如图3-65所示。

3.优越性

变参数螺旋弹簧相对普通螺旋弹簧有其独特的优越性，主要有如下四点：

（1）降低质量

可将顶死在簧座上的端部簧圈做成小圈，且使该部分的丝径变细，因此，无效的“死”材料就相对减少，从而降低螺旋弹簧的总质量。如表3-45所示的中凸双锥、上锥下柱、端锥中柱类组件。

（2）发挥材料潜能

因为可在较小的簧圈上采用较粗的丝径，并可将其节距加大，所以压并这种簧圈的载荷就将变得很大。这就是说，只要不超过许用应力，有限的材料可以造就承受高载荷的螺旋弹簧，从而充分发挥材料的潜能。

（3）应力分布合理

应力随载荷变化的关系，普通螺旋弹簧的增长速率和比应力都是相等的；而变参数螺旋弹簧，其应力增长速率和比应力皆是逐渐变小的，部分变参数螺旋弹簧甚至能使高载荷区段的应力随载荷的变大而减小，这就使材料得以更为合理的利用，如图3-64和图3-65所示。

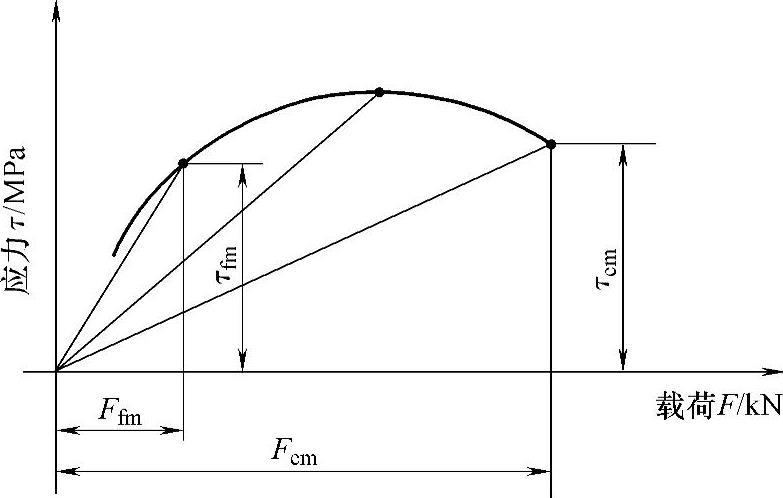
图3-65 特殊变参数螺旋弹簧的应力载荷特性

（4）载荷特性优良

当把具有图3-63特性的变参数螺旋弹簧用于汽车悬架时，便可获得如下优点：

1）可减少变形随载荷变化的幅度，降低乘坐频率的波动范围。

2）在满载载荷、满载簧高以及冲击载荷相同的情况下，变参数螺旋弹簧的变形较小，车身高度降低较小，前照灯跳动轻微。(www.daowen.com)

3）在侧向加速度的作用下，如果载荷转移量相等，那么变参数螺旋弹簧的车身侧倾角较小，反之则可减小横向稳定杆的杆径。

4）在满载载荷和满载簧高相等的情况下，若冲击载荷使其产生等量变形，变参数螺旋弹簧所承受的载荷和所吸收的能量均较大。这就能以较小的悬架变形获得较大的悬架容量。它一方面可减少布置高度，另一方面可减少缓冲块的尺寸。

5）车辆在运行中，在同等回弹量的情况下，变参数螺旋弹簧的压地负荷降低较小，地面附着降低不大，故可相对提高行驶安全性能。

6）评价指标。在有效总质量M、有效圈数n、有效簧高H以及总压缩量f_g等参数大致相同情况下，可以下列指标作为变参数螺旋弹簧技术设计和性能评价的依据。

①比负荷F_M。比负荷F_M是材料潜能是否得以充分发挥的标志。它是末圈压并载荷（全簧压并载荷）F_em与有效总质量M之比（N/kg），即

F_M是单位质量所能承担的最大载荷，故要求越大越好。由式（3-195）可知，在M已确定的情况下，要增大F_M，就得提高压并载荷F_em。普通螺旋弹簧的F_M值较低，而变参数簧在应力容许的条件下，可以向5000N/kg的目标看齐。

②载荷幅度F_r。载荷幅度F_r是螺旋弹簧对载荷变化适应能力的标志。它是末圈压并载荷F_em与首圈压并载荷F_fm的差值与F_fm的比值，即

F_r的值越大越好。F_r值越大，螺旋弹簧对载荷变化的适应能力就越强。普通螺旋弹簧的F_r值为零，而变参数簧的F_r值则可能大于10倍。

③刚度幅度c_r。刚度幅度c_r是载荷变形特性优劣的标志。它是末圈压并点的刚度c_e与首圈压并点的刚度c_f的差与c_f的比值，即

c_r的值越大越好。c_r值越大，意味着载荷变形特性曲线从首圈压并到末圈压并区段的平均斜率越高，频率波动范围越小。普通螺旋弹簧的c_r值为零，而变参数簧的c_r值则可以达到300%以上。

④应力幅度τ_r。应力幅度τ_r能说明各圈压并剪应力τ_km分布的均匀程度，它是最大剪应力τ_ma减去最小压并剪应力τ_mi的差与τ_mi的比值。因此，有

变参数螺旋弹簧的τ_r值可以在0～200%之间变化。τ_r值越小，说明应力分布越均匀，但同时又可能使载荷幅度F_r和刚度幅度c_r变小，故需要综合权衡。

⑤末圈比应力R_eτ。比应力R_τ是各圈压并剪应力τ_km与各圈压并载荷F_km的比值，而末圈比应力R_eτ（MPa/kN）是末圈压并剪应力τ_em与末圈压并载荷F_em的比值，即

R_eτ这个指标是应力分布合理性的标志，是用材水平的体现。设计要求最高应力应在不超过许用应力的前提下尽量提高，设计更希望既能承受高负荷，又能获得低应力。R_eτ值可能小于16MPa/kN。

⑥质量系数M_c。质量系数M_c是说明材料利用率的指标。它是螺旋弹簧无效部分的质量M_d与有效部分的质量M的比值，即

质量系数M_c的数值越小越好。M_c小，说明簧座的死材料少。在座圈数相同的情况下，丝径d和圈径D均发生变化的二变簧就能使M_c的数值降至最小。

4.分析评述

为考查不同种类变参数螺旋弹簧的性能，选择10个典型的元件类型和4个组件类型的变参数螺旋弹簧，对其主要性能指标和评价指标进行对比计算（计算过程从略）。选取元件类型变参数螺旋弹簧的前提条件是：它们的有效质量M、有效圈数n、有效高度H、螺旋角均值α以及总压缩量f_g等参数大致相同。

对比计算螺旋弹簧的种类及结构参数列于表3-46之中。变参数簧的计算过程按顺序列于附表1～附表13之中。

表3-46 对比计算变参数螺旋弹簧的结构参数

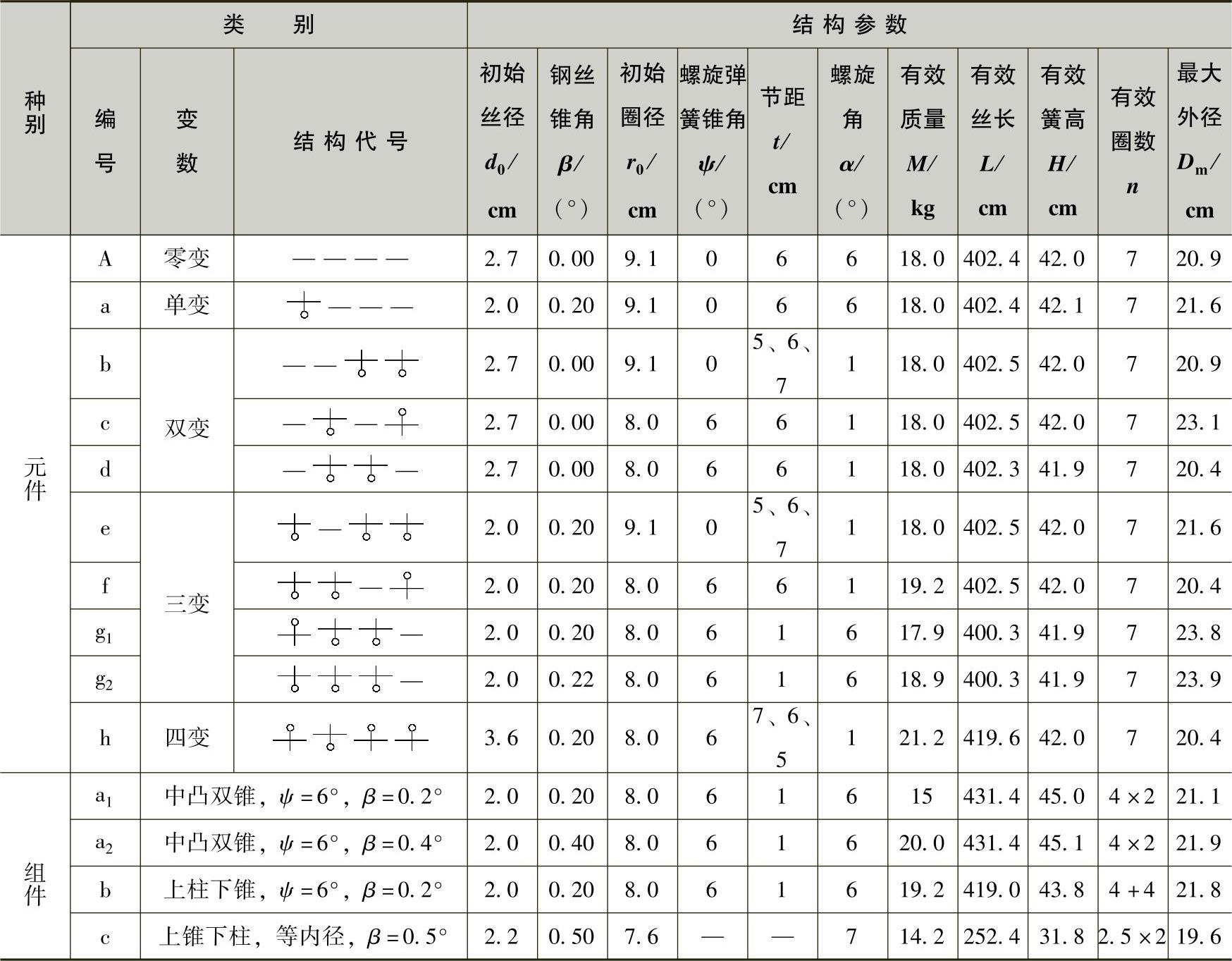
（1）计算结果

对表3-46所列各种类型的变参数螺旋弹簧的主要性能参数和评价指标分别进行了计算，且将计算结果按末圈压并载荷的大小，顺序列于表3-47之中。

（2）性能评述

1）标志性参数。末圈压并载荷，也就是全簧压并载荷F_em，是一个非常重要的标志性的参数。由表3-47的计算结果可知，凡F_em大者，一般说来，比负荷F_M、载荷幅度F_r、刚度幅度c_r、应力幅度τ_r等都大；反之，末圈比应力R_eτ却减小。这就是说，在钢丝质量M等参数相同的情况下，只要能使F_em值增大，就一定能够获得优良的性能参数和评价指标。下面具体谈谈增大F_em值的优点。

表3-47 对比计算变参数螺旋弹簧的性能参数及评价指标

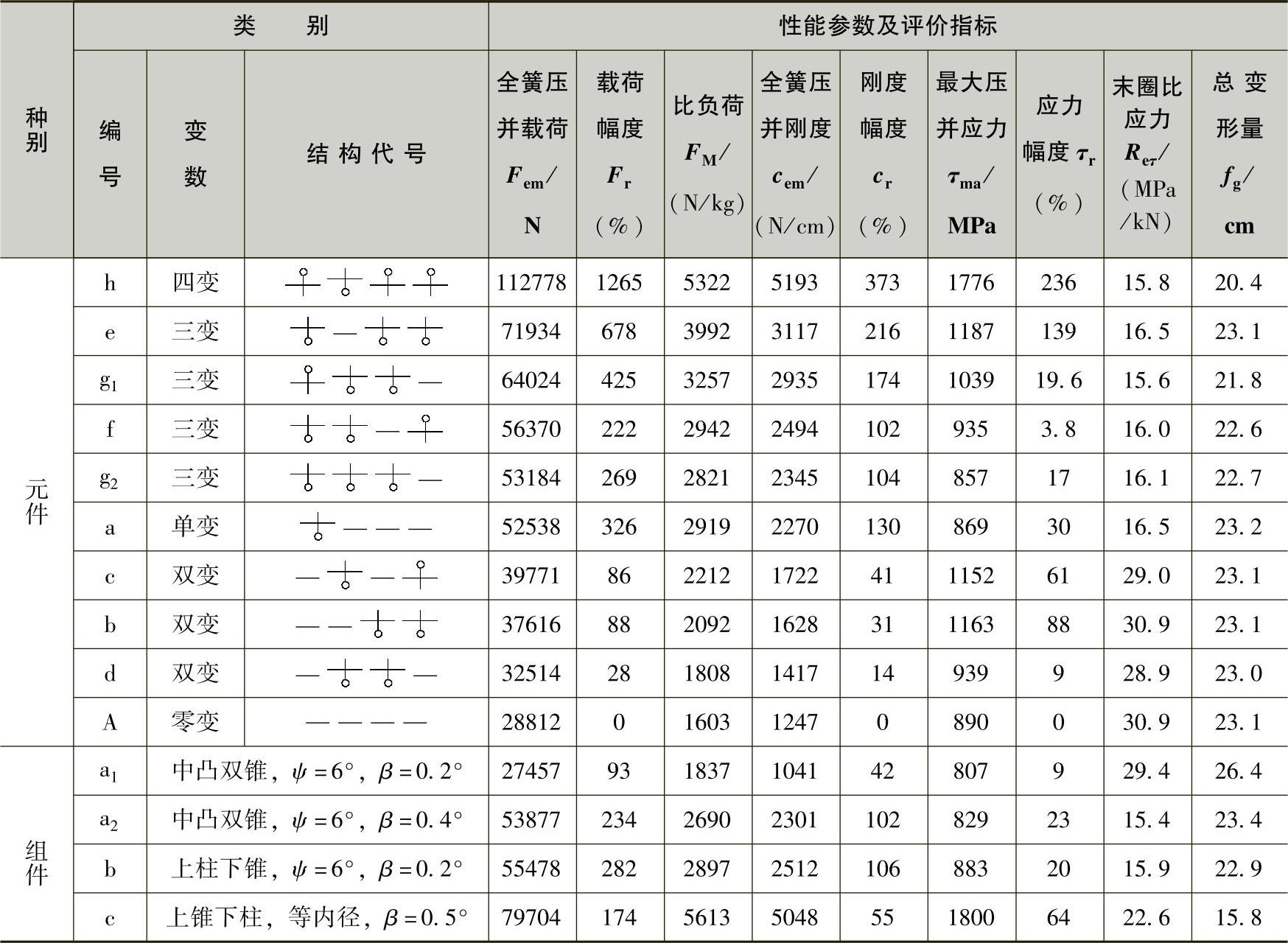
①在有效质量M相同和不超过许用应力的情况下，F_em值增大，说明该螺旋弹簧能够承受较大的负荷，这就充分发挥了材料的潜能。如表3-47中的h、e、g₁、f、g₂和a等类螺旋弹簧的F_em值为52～112kN，比负荷F_M为2.9～5.3kN/kg；然而质量大致相同的c、b、d和A类螺旋弹簧的F_em值仅有29～40kN，F_M值仅为1.6～2.2kN/kg。

②在整簧质量M和总压缩量f_g相同的情况下，F_em值增大，意味着刚度变化的幅度大，因此能获得良好的变刚度特性。如e类簧和d类簧，它们的M值和f_g值均相近，而由于F_em值e类簧为71.9kN，d类簧为32.5kN，故刚度幅度e类簧高达216%，d类簧却仅为14%。

③F_em值增大，能使末圈比应力R_eτ减小，提高合理用材水平。表3-47中的h、e、g₁、f、g₂和a类螺旋弹簧的F_em值均较大，而它们的末圈比应力R_eτ值均在16.5MPa/kN以下。这正是既能承受高负荷，又能相对获得低应力，使材料潜能得以充分发挥的鲜明标志。

F_em值亦不应过分增大，过分增大有可能使最大压并应力τ_ma超过许用应力。表3-47中的h类螺旋弹簧，F_em值达到了112.8kN，比负荷超过了5kN/kg，其最大压并剪应力τ_ma=1776MPa。这个数值超过了相应合金钢的抗拉强度。

此外，提高F_em值主要是靠变丝径的办法来实现的，而变丝径的加工工艺却需要较大的投资。

2）提高F_em值的措施。

提高全簧压并载荷F_em值，实质就是提高螺旋弹簧的性能，提高F_em值的措施，也就是在一定前提下，所应遵循的设计原则和所应选取的设计方案。在设计中，只要懂得结构参数如何影响螺旋弹簧性能，便可掌握获得优良性能的措施。下面具体研究结构参数是如何影响F_em值和螺旋弹簧性能的。

①结构参数对F_em值的独立影响。

当螺旋弹簧有效质量M、有效圈数n和总变形量f_g等参数确定后，要改变F_em值，就得改变丝径d、圈径D、节距t和螺旋角α这四大参数。下面分述这四大结构参数对F_em值的独立影响。

（a）丝径d。丝径d对F_em值有着决定性的影响。由式（3-191）可知，刚度c与丝径d的四次方成正比。在全簧变形量f_g已确定的情况下，也就是F_em与d的4次方成正比。再由表3-47可知，凡是F_em值高的，几乎都是变丝径簧。例如，a类簧与普通螺旋弹簧相比，在圈径D、节距t和螺旋角α都相同的情况下，仅给定钢丝锥角β=0.2°，其比负荷F_M值就比普通螺旋弹簧高了82%。

（b）圈径D。由式（3-191）可知，刚度c与圈径D的三次方成反比。在f_g已定的情况下，也就是F_em与D的三次方成反比。请注意，在变更D的同时，若保持螺旋角α不变，就必然带来节距t的改变，如表3-47中的d类簧；若保持t不变，则又必然引起α的改变，如表3-47中的c类簧。c类簧与同质量的普通簧相比，在D、t不变的情况下，当给定ψ=6°时，其F_M值比普通簧高了38%。改变圈径D对提高F_M值的效果虽不如改变丝径d那么有效，但变更D的圆锥簧能配合变丝径簧的设计，它既可调节应力幅度，还能使端部半径变小，降低无效簧圈的质量。特别是能制成无簧圈叠压的圆锥簧，在不影响总变形量f_g的情况下，降低弹簧高度。

（c）节距t。节距t的改变，也能使F_M值提高。如表3-47中的b类簧，它是在普通螺旋弹簧的基础上，仅将各圈的节距t=6cm，改为5、6、7（5×2+6×3+7×2）cm三种节距，其F_M值就提高了31%。需注意的是，在d和D不变的情况下，t不可能单独变动；变更t，必然伴随着α的变动，参见表3-47中的b类簧。

（d）螺旋角α。螺旋角α的改变，同样能使F_M值提高。α和t同样是相关联的，无论是柱簧还是锥簧，只要改变α，就必然改变t，因而也必将改变F_M值。值得注意的是，b类簧是给定t，让α随其改变；反之，也可给定α让t随其改变。

②结构参数对F_M值的组合影响。

丝径d、圈径D、节距t和螺旋角α这四大结构参数的变与不变、从小变到大/从大变到小和变化速率——这三者不同组配，将可获得不同的设计。如何进行合理组合，获得满意的螺旋弹簧特性，这是大有文章可作的！

由上述研究可知，四大结构参数对F_M值的影响是：使其近似与t和α的一次方成正比，与D的二次方成反比，与d的四次方成正比。据此便可得出如下原则：要增大压并载荷F_em，提高刚度c随钢丝长度L的变化幅度，首先应使丝径d随L变化；其次是当d的变化方向确定之后，圈径D应与其反向变化，节距t和螺旋角α应与其同向变化；最后是提高d和D的变化速率，即加大β值和ψ值。反之，若想降低F_em值，减少c的变化幅度，则应反其道而行。

仔细观察一下表3-47中的几类螺旋弹簧，便可深入理解上述原则。

A类簧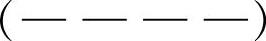是零变元件簧，其F_em值最小，性能最差。

在A类簧的基础上，若将丝径d按β=0.2°从小变到大，那它就变成了a类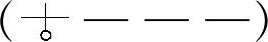单变元件簧，其F_em值提高了82%，各种性能大为提高。

在a类簧的基础上，让圈径D按ψ=6°由小变到大，并让节距t相应由小变到大，那它就变成了g₂类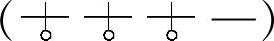三变元件簧，此时，F_em值虽然提高1%，而比负荷却降低了4%，刚度幅度降低了25%。这是因为丝径d的从小变到大和圈径D的从小变到大，二者起了相互抵消的作用。

在g₂类簧的基础上，若让丝径d从大变到小，那它将变成g₁类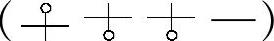三变元件簧，其F_em值增加20%，比负荷增加16%，刚度幅度增加67%。这是因为丝径d的从小变到大和圈径D的从小变到大，二者起了相互增补加强的作用。

在g₁类簧的基础上，若让节距t从大变到小（螺旋角也随之从大变到小），那它将变成了h类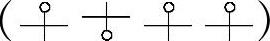四变元件簧，其F_em值增加76%，比负荷增加63%，刚度幅度增加114%，各种性能达其最高水平，这是因为四大结构参数均起相互增补作用的结果。然而，此类簧须选好钢丝锥角β和弹簧锥角ψ的数值，防止应力超标。特别是因端部簧圈丝径最大，增加了座圈部分的“死”材料，故在一般情况下，此类设计是不可取的。

作为组件类螺旋弹簧，表3-45中的e类簧和a类簧应作为组合优选对象。如果在这两类簧的基础上，再把它设计为等内径簧，那将具有工艺简单，便于在中部安装物件以及降低座圈“死”材料等优点。

5.试验验证

本书着眼于变参数螺旋弹簧的性能评述，故对数10类螺旋弹簧计算模型的考核则难以一一例证。下面仅将较为典型的美军高机动多用途轮式车（HMMWV）系列中的1.5t级越野车后悬架螺旋弹簧进行验证。

该悬架螺旋弹簧是变丝径、等内径、上锥下直组合式，其主要结构参数见表3-46。试验和计算的载荷变形特性曲线均绘于图3-66之中。

计算数据与试验数据比较，在变刚度区段各点相对偏差的均值约为8%。

6.结论

变参数螺旋弹簧除能获得令人满意的刚度特性和优良的应力特性外，还能获得足够大的压并载荷，充分发挥材料潜能；采用变丝径螺旋弹簧是提高压并载荷、获取优良性能的关键，而各种结构参数的合理匹配则又可以获得不同的性能，以满足不同的需要；等内径、变丝径螺旋弹簧具有独特的实用价值，应予以优先采用。