本书所研究的螺旋弹簧是为汽车悬架服务的,所以只包括普通的圆柱压缩螺旋弹簧,不包括拉伸弹簧,更不包括扭转弹簧。准确来说,普通圆柱压缩螺旋弹簧,是指四大参数(丝径d、圈径D2、节距t以及螺旋角α)均不随钢丝展开长度L变化的螺旋弹簧。
下面推导普通压缩螺旋弹簧的变形、刚度及应力公式。
1.变形及刚度
(1)单圈簧的变形
当载荷F沿轴线方向作用于螺旋弹簧时(图3-62),螺旋弹簧钢丝截面主要受到扭矩Tt的作用,即
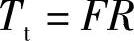
弹簧的轴向变形量为
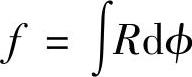
式中 dϕ——钢丝在扭矩Tt作用下的微元角位移,它跟扭矩Tt和钢丝长度ds成正比,
跟材料属性G和材料几何特性JP成反比,即

式中 ds——钢丝的微元长度,ds=Rdθ;
R——螺旋弹簧中径之半;
dθ——微元极角;
G——材料扭转模量(N/cm),G=7.94×106N/cm;
JP——钢丝的极惯性矩,JP=πd4/32;
d——钢丝直径。
将有关参数代入上式后积分,便可得到一个单圈的变形:
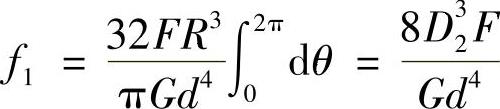
式中 D2——螺旋弹簧中径。
(2)整簧变形量
整根螺旋弹簧的变形量为

式中 n——有效圈数。
(3)整簧刚度

(4)压缩行程
单圈可压缩行程为

整簧可压缩行程为

(5)压并载荷(https://www.daowen.com)
整簧压并时的载荷为

2.剪切应力
普通密圈螺旋弹簧在力F对截面的作用下,因剪切引起剪应力τ′(图3-62),其方向与力F相反,并在截面上均布,故有

扭矩FR使簧杆扭转,在其R所对应的截面上所产生的最大剪应力τ″m发生在该截面的周边,为

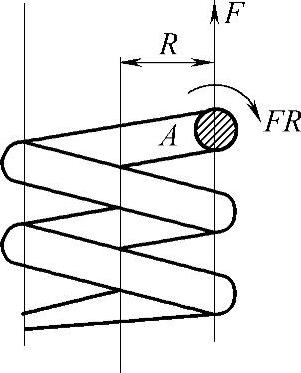
图3-62 剪应力
两项应力相加,即得该截面上的总应力。危险点是τ′与τ″m相重合的点,即断面内侧点A,其最大剪应力为
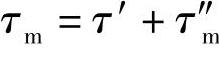

τm尚需进行修正,即

式中 K——曲度系数,或称为应力修正系数,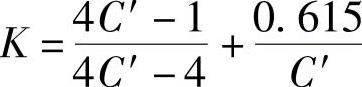 ;
;
C′——旋绕比,C′=D2/d。计算静载荷螺旋弹簧时,可取K=1。
3.计算示例
示例参数:簧载负荷F=3500N,钢丝直径1.5cm,有效圈数n=6,节距t=4.4cm,中径D2=16cm,螺旋角α=5°。
弹簧刚度为
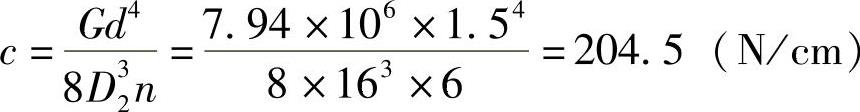
弹簧变形为
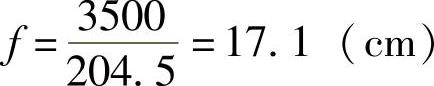
压并载荷为
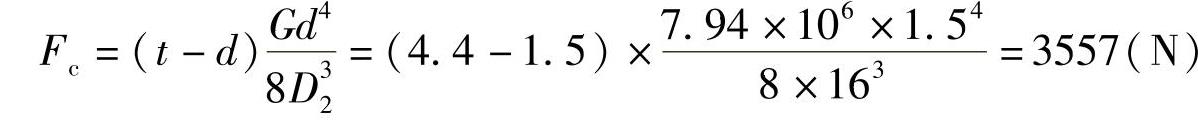
旋绕比为

曲度系数为
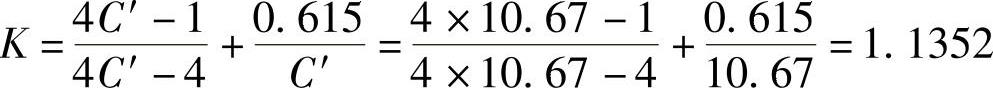
最大剪应力为
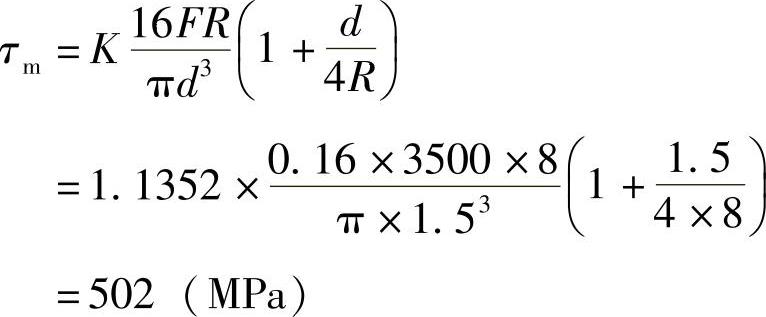
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






