非对称钢板弹簧在一定的汽车轴距下，可以调整前后悬架的长度和轴荷分配，可以改变接近角和离去角的大小，可以协调车桥和发动机的位置矛盾等，而且还具有许多独特的性能。掌握这些性能，对于搞好汽车总布置设计和悬架设计是十分必要的。

1.非对称度

所谓非对称度，就是弹簧主片长度L分配于长边的长度l_L1和短边的长度l_S1之比（图3-56），即

非对称度Y不仅影响弹簧两边的刚度，以及整个弹簧的刚度和角刚度，而且影响悬架相关点的运动轨迹等。Y值过小意义不大，过大也不可取，一般可在1.3～1.5的范围内取值。

2.桥心线处的变形f与两端变形f_S、f_L的关系

在已知短边变形f_S和长边变形f_L的情况下，按照图3-57的几何关系，可以求得桥心线处的变形f的表达式为

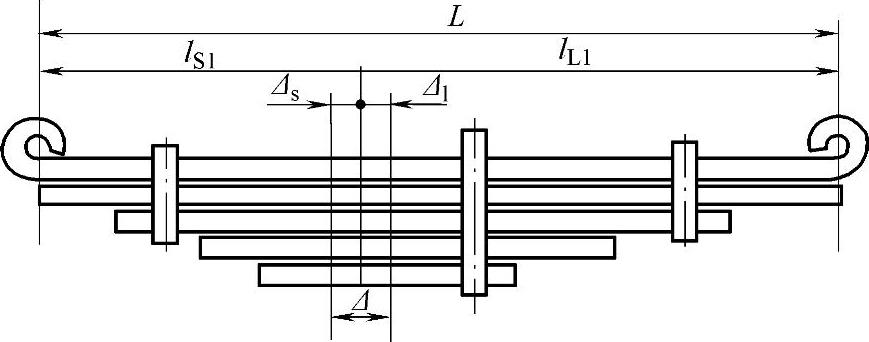
图3-56 非对称钢板弹簧

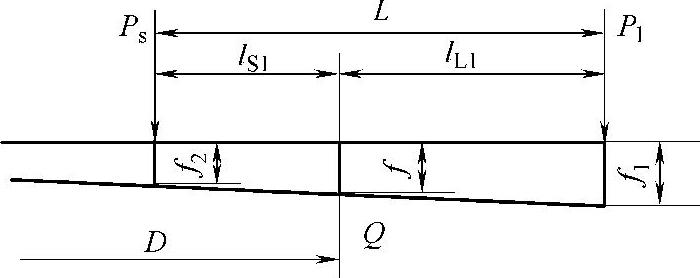
图3-57 两端与桥心线处的变形关系

3.两端变形f_S、f_L与桥心线处变形f的关系

根据设计要求，在已经提出了悬架静变形f的情况下，如何求出分配于两端的变形f_S和f_L呢？这是非对称簧设计必须要解决的问题。

仅知f，利用式（3-156）是不可能求出两个未知数f_S和f_L的。可先求出两端变形的结构表达式，然后再求二者的关系式。由此关系式加上式（3-156），问题就可解决了。

假设弹簧各片长度均按非对称度的关系取值，那么两边弹簧的片数、片宽和片厚均相等，故作为传统式弹簧的形状系数δ两边亦相同。所以，两端变形可分别表示为

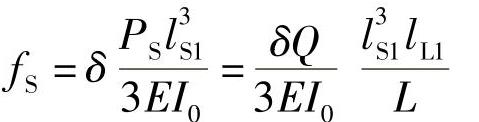
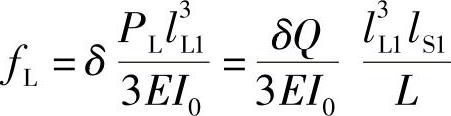
式中 P_S、P_L——作用于短端和长端的力；

Q——簧载负荷；

L——主片长度；

l_S1、l_L1——主片分配于短边和长边的长度。

两端变形比为

由式（3-156）和式（3-157），可以推得两端变形与桥心线处变形的关系式为

短端变形：

长端变形：

4.两边刚度c_S、c_L与桥心线处刚度c_F的关系

两边刚度为

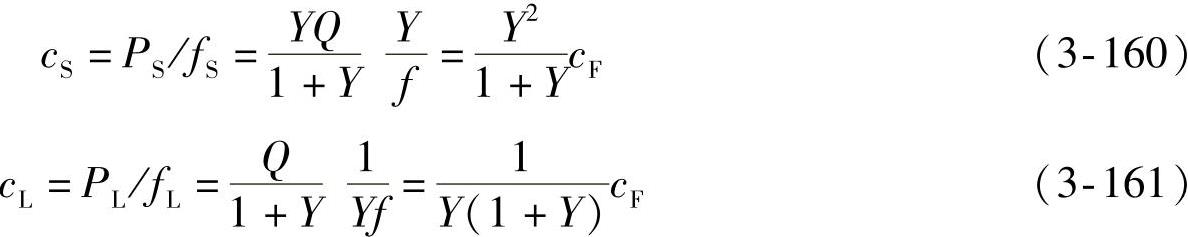
反之，可求得桥心线处的刚度为

两边刚度比为

5.对称簧的变形f_D、刚度c_D与非对称簧的变形f_F、刚度c_F的比较

在弹簧主片相同，片数、片宽、片厚以及形状系数均相同的前提下，对称簧与非对称簧在桥心线处的变形及刚度谁大谁小呢？作为变形，由于

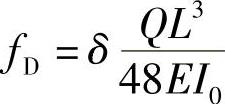
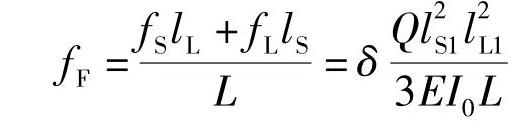
所以，对称簧与非对称簧的变形比为

由于Y>1，故由式（3-164）可知

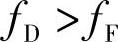
对称簧与非对称簧的刚度比为

由于Y＞1，所以有

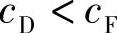
6.对称簧与非对称簧角刚度的比较

此处所指的角刚度，包括两个内容：一为抵抗车桥角位移的弹簧自身的角刚度c_θ；一为抵抗车身横向角位移的悬架横向角刚度c_α。

（1）弹簧自身角刚度c_θ

对于对称簧，有

对于非对称簧，有

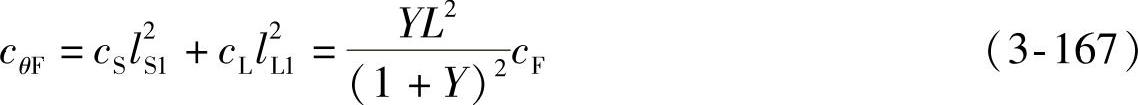(www.daowen.com)

对称簧与非对称簧自身角刚度比为

由于Y＞1，故由式（3-168）可知

观察式（3-165）和式（3-168），还可顺便得到

（2）悬架横向角刚度

对于对称簧，有

式中 k——弹簧自身的抗侧倾能力；

B——左、右板簧中心距。

对于非对称簧，由于车身横向倾斜时，固定于车轴上的左右弹簧座不可能倾斜（车轴承受一个附加力矩），故非对称簧的短、长部分只许独立地参加工作，所以其横向角刚度应为

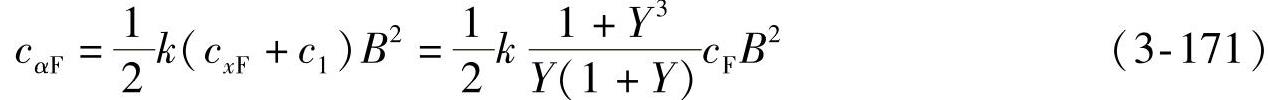
对称簧与非对称簧的横向角刚度比为

由于Y＞1，故由式（3-172）可知

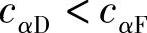
当Y=1.5时，其比值约为0.79。由此可见，在弹簧线刚度低、左右弹簧簧心距又小的情况下，采用非对称簧以加大横向角刚度是较为有效的。

7.运动关系

汽车行驶、车桥跳动时，对称簧各相关点只能作平行移动，而非对称簧则可绕着一个所谓的偏摆中心摆转。

偏摆中心至桥心线的距离D可由图3-57所示的几何关系求得。

由于

将式（3-157）代入上式，便可得到

大家知道，非对称簧相关点（刚化于车桥上的所有的点）的运动瞬心和轨迹半径是利用“三连杆机构”作图求出的。Y值大时，可按中心扩展法作图；Y值小时，则按两点变形法作图。详见第三章第一节。

本书着重指出的是非对称簧与对称簧的不同之处。

作为对称簧，车桥跳动时，各相关点的运动轨迹半径，均和弹簧主片中点的运动轨迹半径R相等。若设实际夹紧长度为S，则有

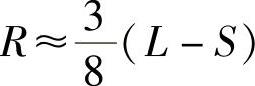
非对称簧则不然，不同的相关点有着各自的轨迹半径，如图3-58所示。

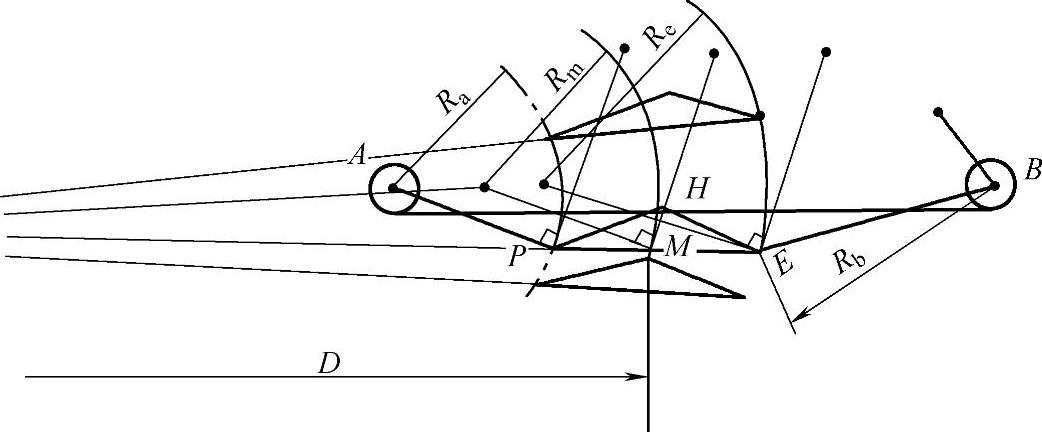
图3-58 非对称簧相关点的运动轨迹

在图3-58中，相关点E的轨迹半径R_e就比相关点M的轨迹半径R_m要大，而R_m又大于R_a等。非对称簧的这一特点，对于某些总成部件的安装来说，提供了较大的选择余地。如减振器的下支点，随着布置位置的不同，阻尼力矩就不一样，因为阻尼力矩等于阻尼力F乘以阻尼力臂R。而力臂R是和下支点的轨迹半径紧密相关的。在一定的减振器布置角度下，轨迹半径越大，阻尼力臂也就越大。

8.各片长短及其在两边的分配

当主片长度L、非对称度Y以及夹紧长度Δ确定以后，还需确定各片长度以及各片长度和夹紧长度在两边的分配。

对于各片长度L_k，建议按照图3-59所示的几何关系，由式（3-174）确定。

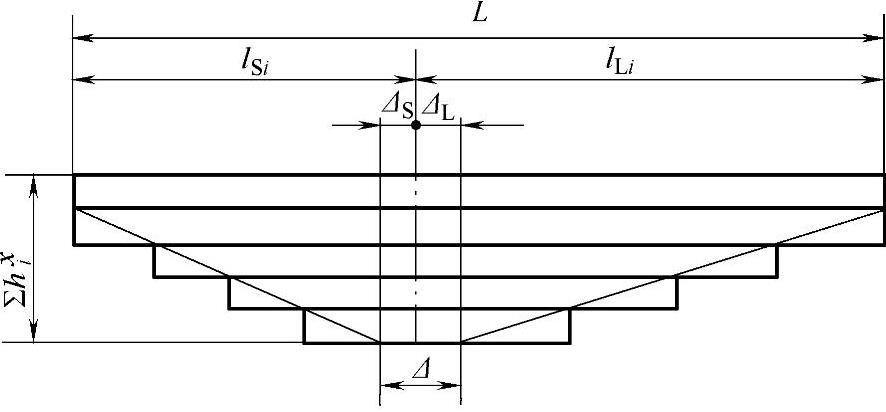
图3-59 非对称簧的几何关系

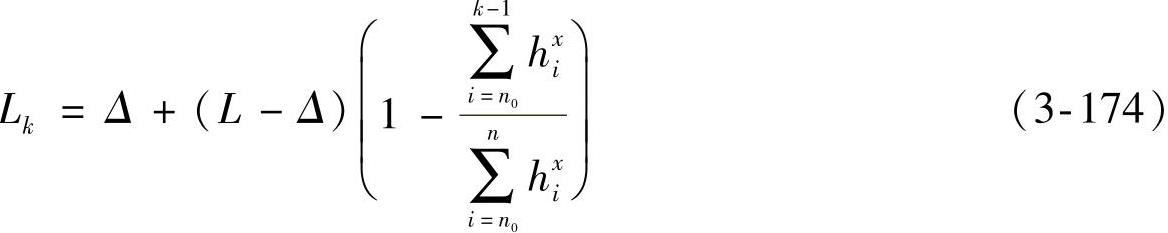
式中 n——总片数；

n₀——主片重片数；

h_i——各片厚度（cm）；

Δ——夹紧长度（cm）；

x——厚度指数。

指数x的取值应视情况而定。当x=3时，符合等强度规律，但此时末片较长，根部应力较大。特别在非对称簧的情况下，短边片间长度差太小，故建议x可在1.5～2.5取值。

各片长度L_k可按式（3-175）和式（3-176）分配于两边。

短边长度为

长边长度为

夹紧长度Δ亦可利用式（3-175）和式（3-176）两式进行分配。