变断面钢板弹簧由于具有合理利用材料等优点,故在汽车悬架中,特别在那些批量生产的产品上早已得到了普遍的采用。本书拟在一般的情况下,研究建立图3-42所示的直线型和抛物线型两种变断面钢板弹簧的设计计算方法。
讨论研究的具体内容:单片变形、片端力、总成变形及刚度、总成应力、单片弯矩和应力、曲率半径及簧体质量。

图3-41 各片弯矩
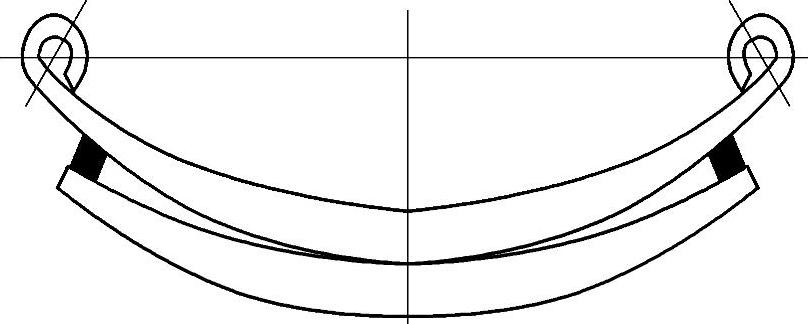
图3-42 变断面钢板弹簧结构示意
1.单片变形
利用作用于单片弹簧端部的力Pk,不仅可以确定各片的弯矩Mxk和应力σxk,而且还可确定整副弹簧的变形f。然而研究单片弹簧在外力作用下的变形,则是确定各单片端部受力的必不可少的工作。
研究的第k单片弹簧的变形时,无论是直线型或抛物线型,均有如下几种情况:
①求在力Pk作用于lk处时,lk+1处的变形fak。
②求在力Pk+1作用于lk+1处时,lk+1处的变形fbk。
③求在力Pk作用于lk处时,lk处的变形fck。
④求在力Pk+1作用于lk+1处时,lk处的变形fdk。
下面仅以直线型变断面簧中的A种情况(图3-43)为例来推导其单片变形表达式,至于其他7种情况,为节约篇幅,此处不予推导。
8种情况变形表达式的推导结果见表3-24和表3-25。
图3-43表达了直线型变断面簧第k单片的结构情况。Δk所示的直线段起夹紧作用。为了制作卷耳或装设片间支垫,片端制成一个平直部分。为简化力学分析,该平直部分中的下部左边(三角形)部分予以忽略。
在图3-43全片簧的长度上,其变厚度部分x断面处的厚度为

图3-43 直线型A种情况的变形

式中
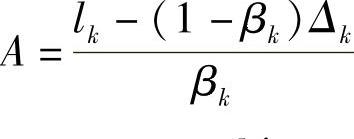
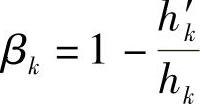
x断面处的惯性矩为

式中 Ik——根部惯性矩,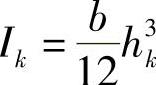 ;
;
b——弹簧片的宽度。
若将力Pk平移至lk+1处,那么作用于x断面处的弯矩为
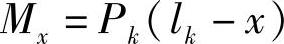
单位弯矩
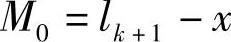
根据莫尔定理,lk+1处的变形为
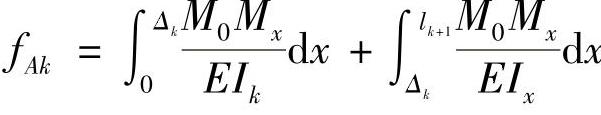
经积分整理后得到表3-24中的fAk式。
2.片端力
所谓片端力就是主片端部在力P1的作用下,各片端部所受的力。推求片端力,不仅是为了计算各片的弯矩和应力,而且还可借助片端力推求整副弹簧的变形和刚度。
按照集中载荷的假设(在有片间支垫的情况下,这种假设是完全符合客观实际的),利用表3-24和表3-25中的A、B、C和D四种单片变形公式,便可参照图3-44来建立n片弹簧片端力的计算公式了。
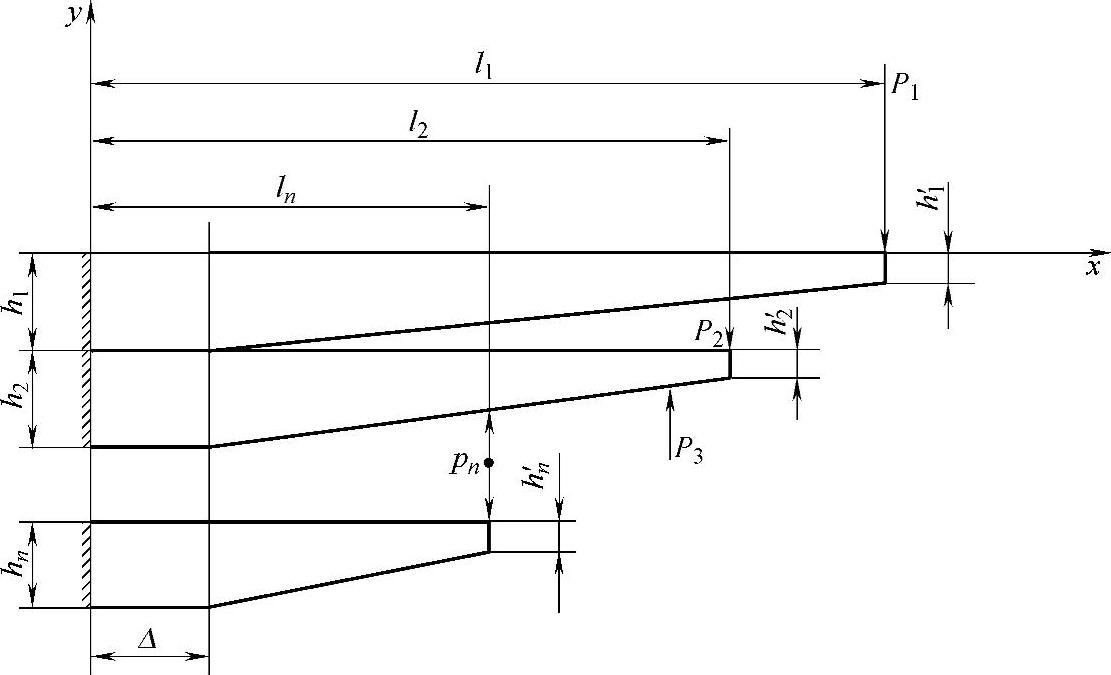
图3-44 变断面簧的片端力
由图3-44可知,对于第k和第k+1片的接触点可建立如下等式:

即
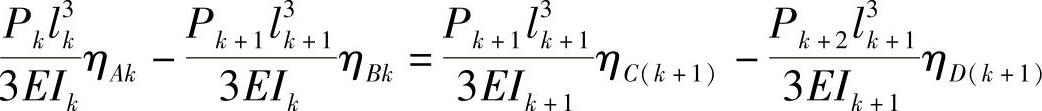
整理后得到
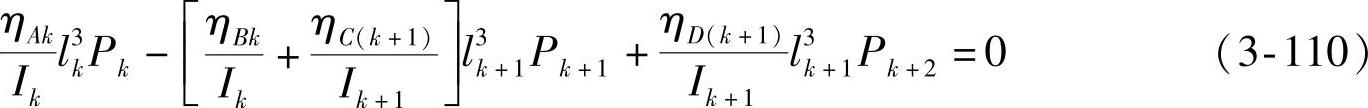
或
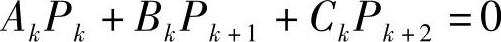
这是一个(n-1)个方程构成的方程组,解此方程组可以得到各片片端力Pk(N)的表达式为
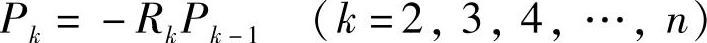
式中

注意:对式(3-110)中的系数ηAk、ηBk、ηCk和ηDk,直线型变断面簧按表3-24公式计算,抛物线型变断面簧按表3-25计算。
表3-24 直线型变断面簧单片变形公式
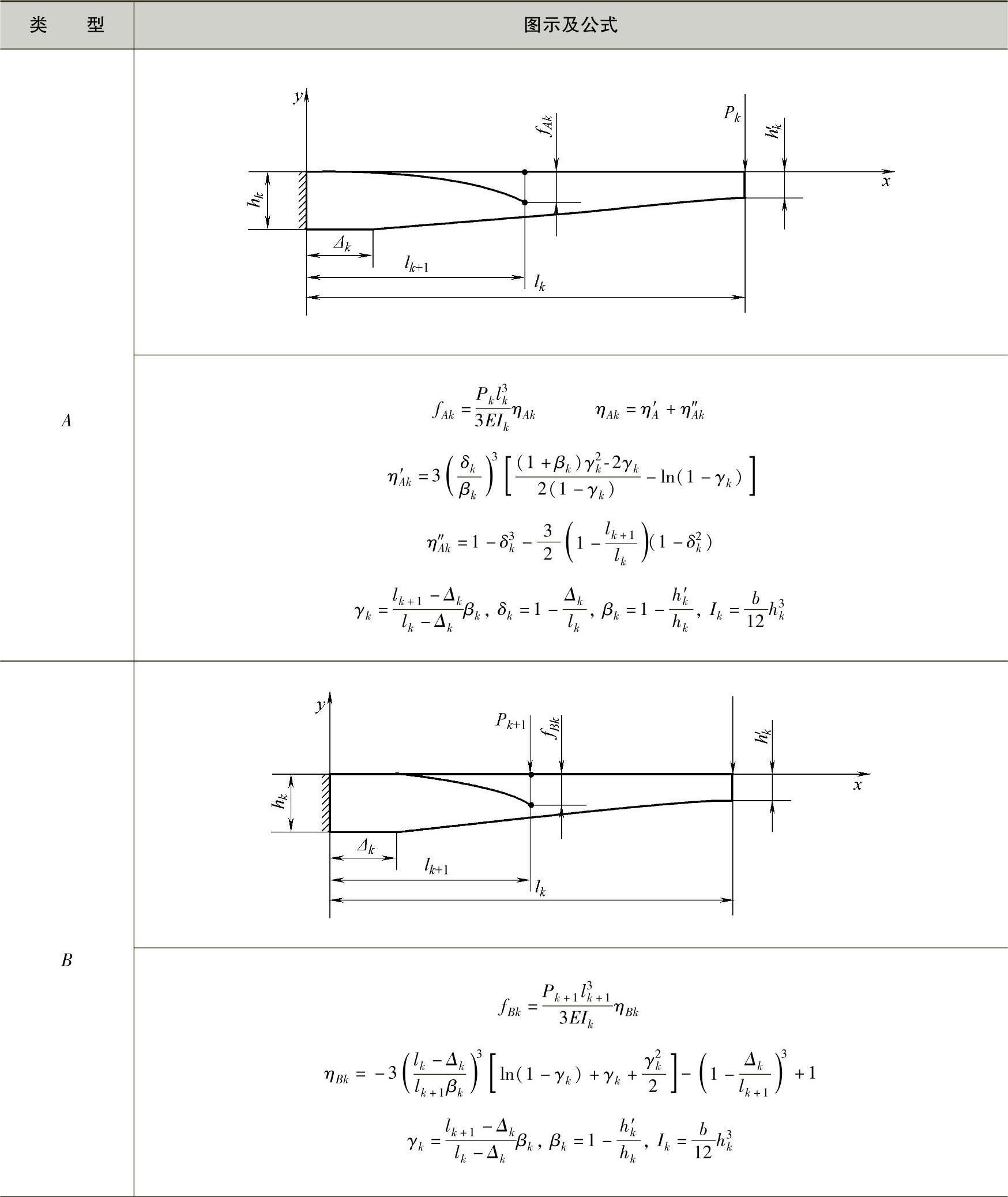
(续)
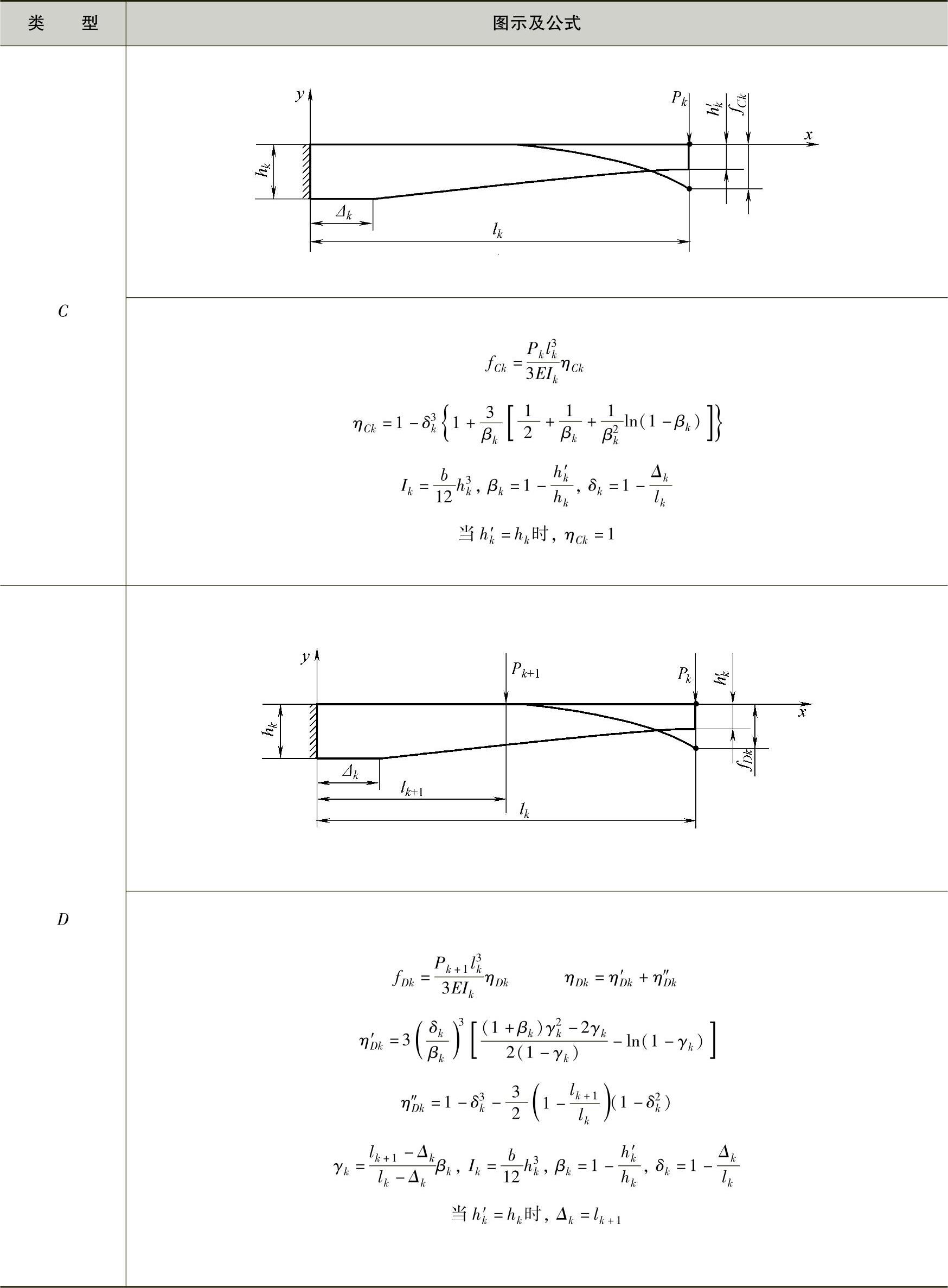
表3-25 抛物线型变断面簧单片变形公式

(续)

3.变形及刚度
因为变断面簧的断面厚度是随x坐标变化的,所以要按一般方法准确求出各片并非等长的整副弹簧的变形则是相当困难的。然而,“主片变形法”却是一个既简单又准确的方法。所谓“主片变形法”,就是利用已知的作用于主片的片端力(计算单片应力必须计算片端力{来计算主片端部的变形。主片端部的变形就是弹簧总成一端的变形。
由图3-45可知,主片除在端部l1处受有一个向下的力P1外,还在第二片端部l2处受有一个向上的力P2。主片的变形应是这两力合成作用的结果。利用表3-24和表3-25中的单片变形公式C和D可以得到
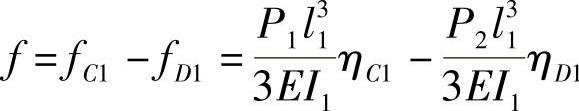
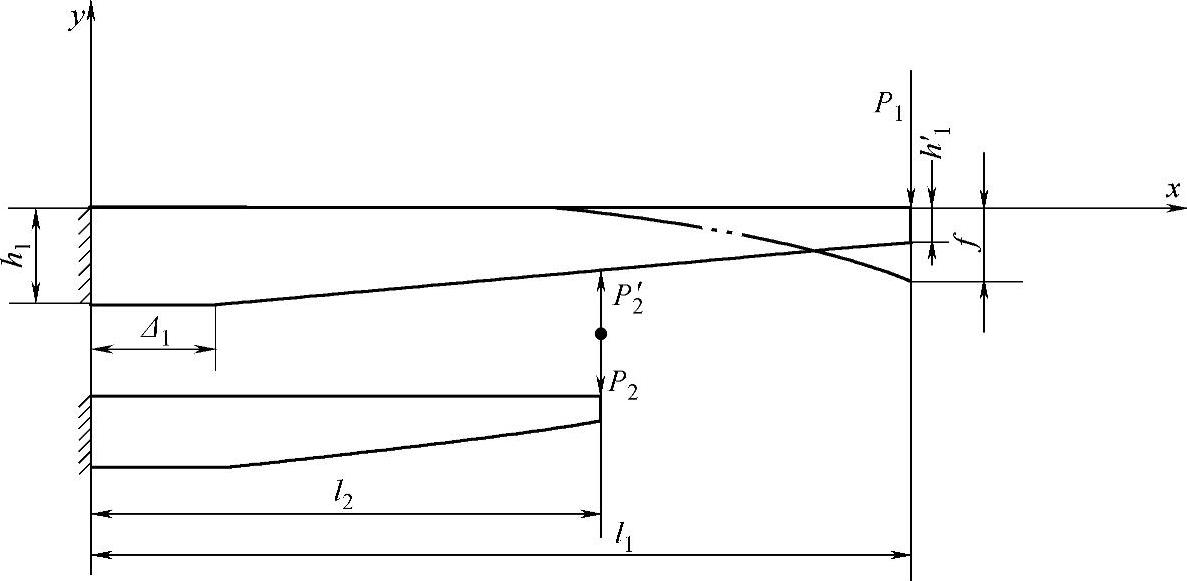
图3-45 主片的变形
所以,弹簧总成一端的变形为

由式(3-111)可得整副弹簧的自由刚度c0(N/cm)

式中 E——抗弯模量,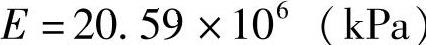 ;
;
α——修正系数,可取α=0.92~0.94;
l1——主片长度之半(cm);
I1——主片端部惯性矩, ;
;
ηC1、ηD1——系数,可按表3-24和表3-25中的C、D两式计算;
P1、P2——第1、2片的片端力,在用式(3-110)计算片端力Pk时,P1可取为单位力。
4.总成应力
为计算总成根部静应力σA(MPa),可直接用集中载荷法的各片根部应力的平均值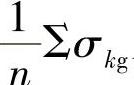 来代替总成应力,即
来代替总成应力,即
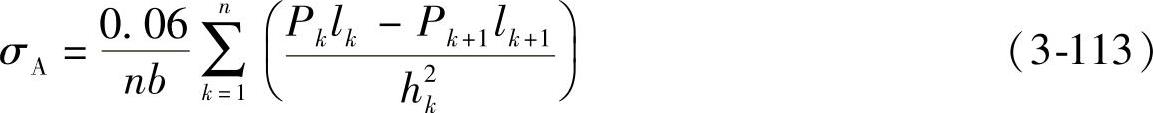
式中 lk——各片有效长度之半(cm);
hk——各片根部厚度(cm);
总成应力计算值不得超过许用应力的75%。
5.单片弯矩和应力
利用已知的片端力Pk,便可求出各片任意断面的弯矩和应力。各片任意断面的应力σkx(MPa)为

式中 Wkx——各片任意断面的断面系数。
 时,有
时,有
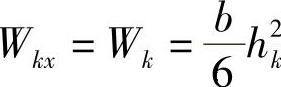
当 时,分两种情况。
时,分两种情况。
对于直线型,有
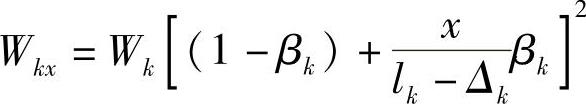
对于抛物线型,有
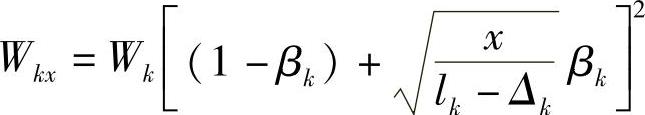
式中 βk——各片断面因子,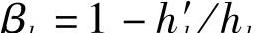 ;
;
Δk——各片根部平直段长度之半(cm)。
当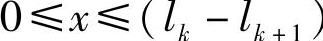 时,有
时,有

当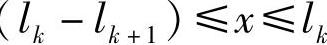 时,有
时,有
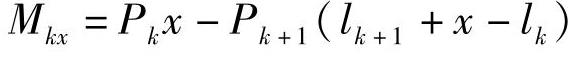
式中 Mkx——各片任意断面的弯矩(N·cm);
注意:计算弯矩时,x应从各片片端计起。
6.曲率半径
曲率半径包括总成曲率半径R和单片自由曲率半径Rk。为建立它们的计算公式,必先建立变断面簧在中心螺栓系紧后各片预弯矩M0k与各片自由曲率半径的关系式。
(1)预弯矩表达式
假设钢板弹簧在中心螺栓系紧后,各片保持着单一圆弧状态,那么全片的预弯矩M0k(N·cm)和势能改变量Uk有着如下的关系:
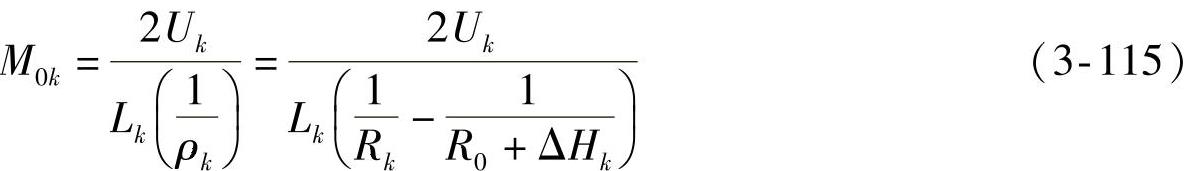
式中 Lk——各片总长度(cm);
1/ρk——各片曲率改变量;
ΔHk——总成曲率半径的增量,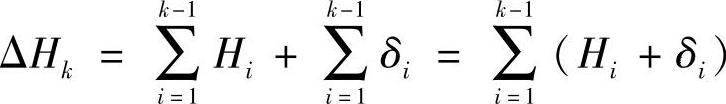 。其中Hi为第
。其中Hi为第
i(k)片片间支垫处的厚度(cm);δi为第i片支垫的厚度(cm)。对于直线型,片间支垫处的厚度Hi为

对于抛物线型,片间支垫处的厚度Hi为
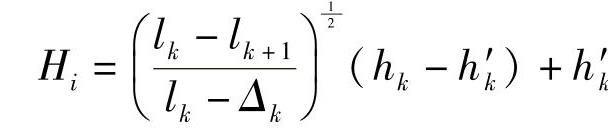
由式(3-115)可知,为了求得预弯矩,必须先找出各片的势能改变量。下面先推求两型变断面簧的单片势能改变量,然后确定预弯矩表达式。
①直线型变断面簧。
由图3-46可知,直线型变断面簧单片的x断面处的厚度为
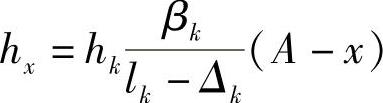
式中
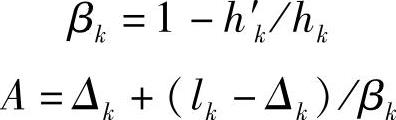
x断面处的惯性矩为

由此,x断面处的变形能可表示为
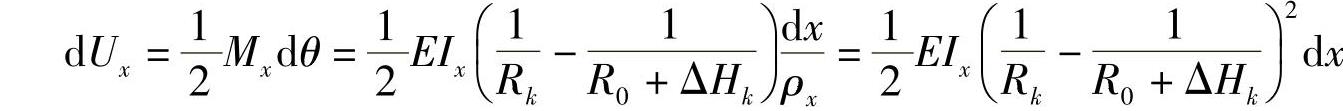
整片变形能为
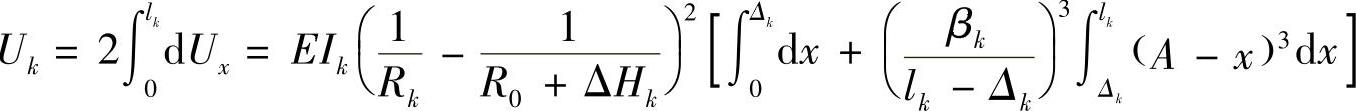
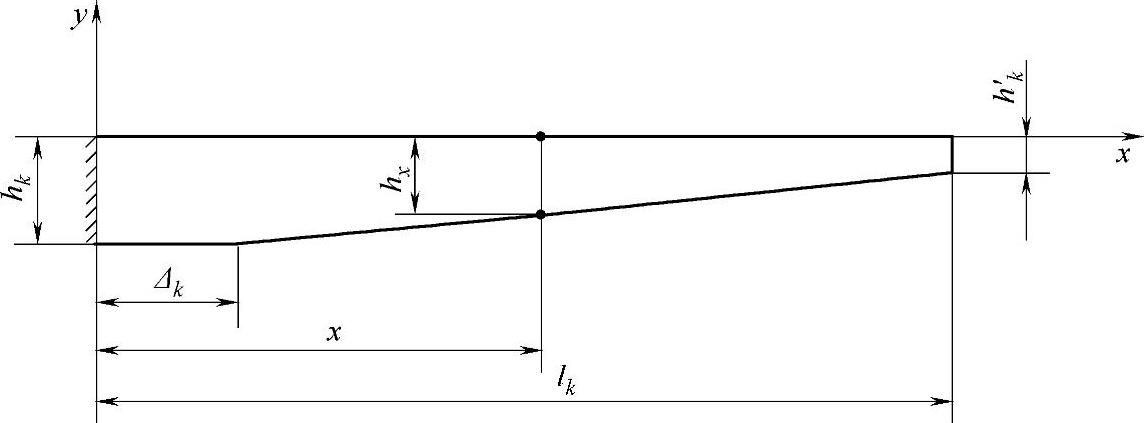
图3-46 直线型单片
经积分后得到

式中 Ak——直线型变断面簧各片结构因式,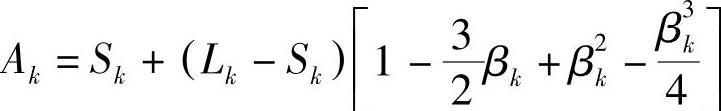 ;
;
Sk——中部平直段的总长度(cm)。
将式(3-116)代入式(3-115),便可得到各整片的预弯矩M0k(N·cm)为

②抛物线型变断面簧。
由图3-47可知,抛物线型变断面簧单片其x断面处的厚度为


图3-47 抛物线型单片
x断面处的惯性矩为
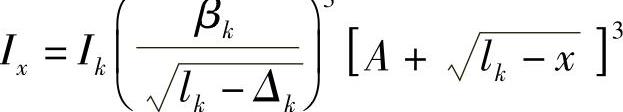
式中
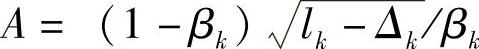
由此可知x断面处的变形能为
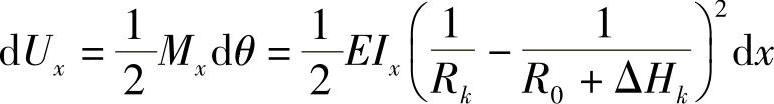
整片变形能为
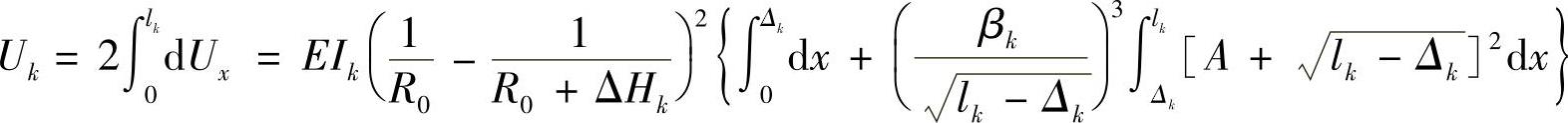 (https://www.daowen.com)
(https://www.daowen.com)
经积分后得到
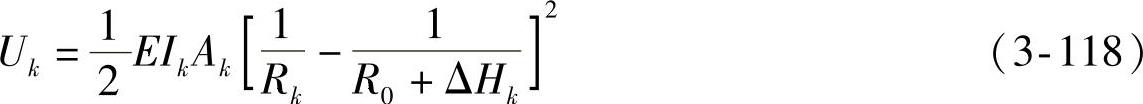
式中 Ak——抛物线型变断面簧各片结构因式(cm),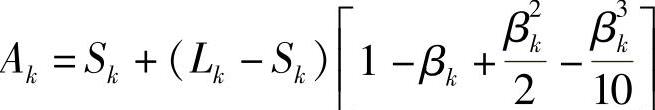 。将式(3-118)代入式(3-115)便可得到各整片的预弯矩M0k(N·cm)为
。将式(3-118)代入式(3-115)便可得到各整片的预弯矩M0k(N·cm)为

(2)预弯矩的分配
为了确定各片的自由曲率半径Rk,除须建立预弯矩表达式外,还须给定各片的预弯矩。
预弯矩的分配给定是和总片数n有关的。当n≤4时,各片预应力σ0k的弯矩M0k可参照图3-48的方法确定。
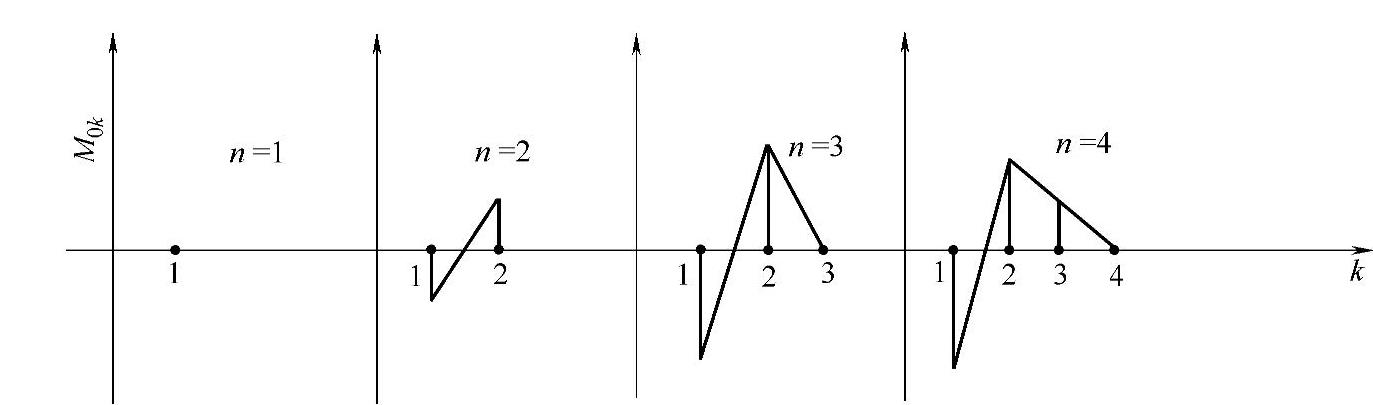
图3-48 少片簧预弯矩的分配
当n=1时,预弯矩M01=0,单片自由曲率半径就是总成曲率半径,即R1=R0。
当n=2时,由于第2片就是最末片,为避免其根部工作应力过大,第1片的负值弯矩M01应适当取小,乃至基本上不给预弯矩。为简化工艺,可考虑将第1片和第2片的曲率半径取成一样,即
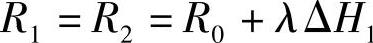
式中 ΔH1——第1片总成曲率半径的增量(cm),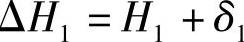 ;
;
H1——第1片片间支垫处的厚度(cm),见式(3-115);
δ1——第1片和第2片间支垫厚度(cm);
λ——厚度ΔH1的分配系数,粗略计算时可取λ=0.5。
当n=3时,主片预弯矩M01(N·cm)按式(3-120)取值;第2片:M02=M01;第3片:M03=0。

式中 W1——主片均值断面系数(cm3);
W1——主片根部断面系数(cm3);
σA——总成静应力,按式(3-113)取值。
对于直线型,W1为

对于抛物线型,W1为

当n=4时,主片预弯矩M01仍按式(3-120)取值;第2片: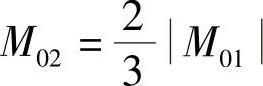 ;第3片:
;第3片: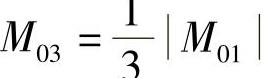 ;第4片:M04=0。
;第4片:M04=0。
当n>4时,主片预弯矩M01按式(3-120)取值,除此以外各片的预弯矩,按多片簧处理。
(3)单片曲率半径
由式(3-117)和式(3-119)两式所确定的预弯矩M0k与单片曲率半径Rk和总成曲率半径R0的关系,便可导出单片曲率半径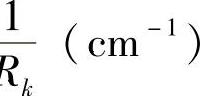 的计算公式为
的计算公式为

式中 α——非单一圆弧系数,见式(3-124)。
(4)总成曲率半径
计算总成曲率半径是悬架设计的需要。在已知各片自由曲率半径Rk和其他结构参数的情况下,可分别按弯矩和为零及和势能最小的假设来推求总成曲率半径R0的表达式。
①弯矩和为零的假设。
式(3-117)和式(3-119)表达的是单片簧的预弯矩,而整副弹簧预弯矩的和为

令∑M0k=0,便可解得

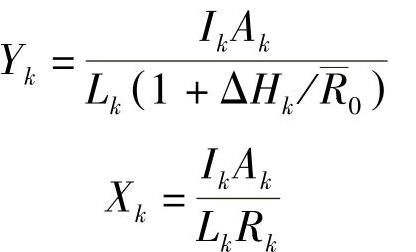
式中 R0——总成曲率半径的初值(cm),可取 。
。
式(3-122)不能直接用以计算,因为各片并不等长,中心螺栓系紧后各片并非皆保持单一圆弧状态。式(3-122)的计算结果必须乘以非单一圆弧系数。
②势能和最小的假设。
式(3-116)和式(3-118)表达的是单片簧的变形能,而整副弹簧的变形能为
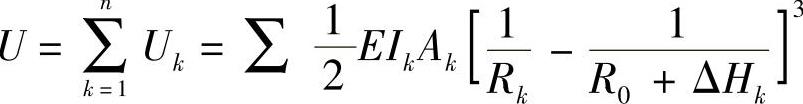
而U对总成曲率半径R0(cm)的一阶导数可近似表示为
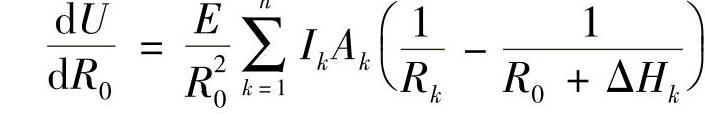
令dU/dR0=0,便可解得

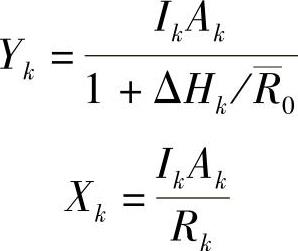
(5)非单一圆弧系数
钢板弹簧各单片在自由状态下各自有一个统一的自由曲率半径Rk0,然而,当中心螺栓拧紧后,各片则产生了若干个新的曲率半径。在同一片上,新的曲率半径的个数从最末一片算起直至主片,依次是1、2、3…(n-1)、n。
式(3-117)和式(3-119)是变断面梁弯曲的基础公式。然而,它们是有条件成立的,那就是各片单一圆弧的假设。即当中心螺栓拧紧后,在假设总成曲率半径为R0的情况下,各片所有断面的曲率改变量皆为
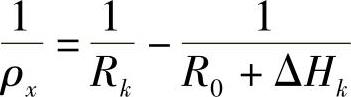
多圆弧的存在和单一圆弧的假设显然是相矛盾的!为协调这一矛盾,减少设计偏差,故在确定各单片自由曲率半径Rk的式(3-121)中引进了一个修正系数α,称为非单一圆弧系数。下面分别确定设计用和验算用的α的计算公式。
①设计用。
确定各单片的自由曲率半径Rk是钢板弹簧设计中的重要内容之一。然而,由式(3-121)可知:要确定Rk,除需给定预弯矩M0k之外,尚需给出α值。
如何确定α值呢?这只需将式(3-121)代入式(3-123),并近似认为R0=R0,则可得到

②验算用。
在各单片自由曲率半径已经确定的情况下,为了了解各片中的预弯矩和预应力,就必须知道非单一圆弧系数α的数值。
由于弯矩和为零的假设与单一圆弧的假设是相应的,加之认定势能和最小的假设是可信的,故可将式(3-123)与式(3-122)之比视为非单一圆弧系数,即


7.簧体质量
如何降低弹簧总成的质量m,是弹簧设计的任务之一。簧体质量m(kg)的计算公式为

式中 Mk——各片质量因式;
ρ——密度(g/cm3)。
对于直线型,Mk为
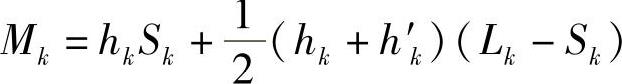
对于抛物线型,Mk为
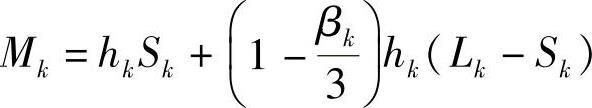
8.结语
变断面簧的计算方法具有如下几个特点:
①能够计算总变形、应力及曲率半径等一系列参数,具有较为完整的系统性。
②各片弹簧不管是否等长均能计算,具有满足各种设计要求的普遍性和灵活性。
③采用“主片端部变形法”建立总成刚度表达式,其方法是以简代繁,其效果是提高了计算精确性。
④采用“非单一圆弧系数”修正各片曲率半径,能够保证各片预弯矩和为零,这不仅具有理论意义,而且在片数稍多的簧中也有其实际意义。
9.计算示例
(1)约束条件
主片长度L1=135mm,总成负荷P=9800N,总成静挠度f=10cm,总成曲率半径R0=160cm,总成质量m≤27kg,总成应力σA≤450MPa。
(2)计算程序
1)设想方案。
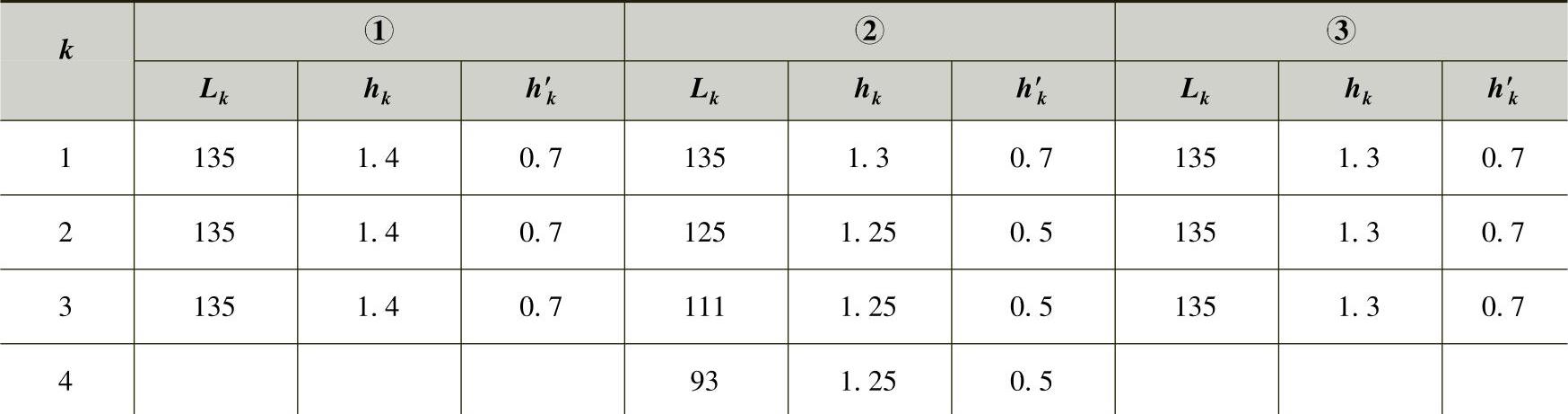
初步提出3个方案共6组弹簧。各方案的簧宽b皆定为7.6cm,中部平直段的长度Sk=2Δk一律取为10cm,至于各片总长度Lk、根部厚度hk以及端部厚度h′k等参数见表3-26。
表3-26 设想方案 (单位:cm)
2)计算总成质量。
总成质量m由式(3-126)计算,其中密度ρ取为7.8g/cm3。计算结果见表3-27。
表3-27 总成质量

由表3-27数据可知,直线型均未超重,抛物线型仅方案③未超重。
3)计算各片片端力。
各片片端力Pk由式(3-110)计算,计算结果见表3-28。
表3-28 各片片端力
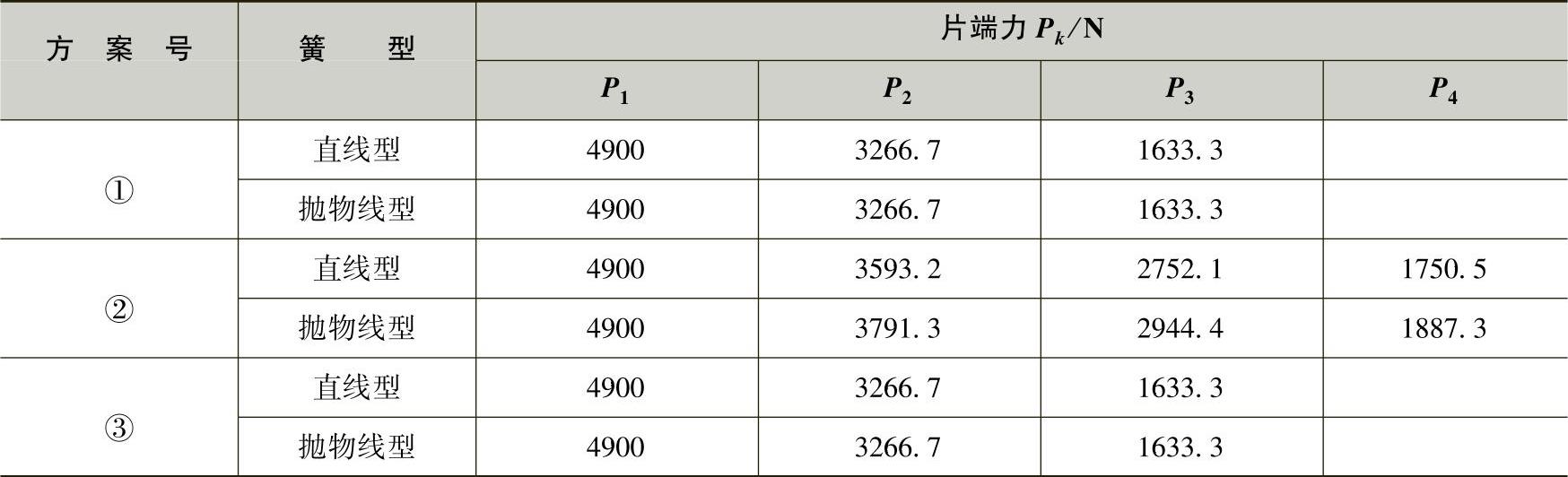
表3-28的数据说明,在同一簧中,若各片几何参数相同,则片端受力相同。
4)计算总成自由刚度及变形。
总成自由刚度c0用式(3-112)计算。式中的修正系数α可取为0.9。计算结果及总成变形f见表3-29。
表3-29 总成自由刚度
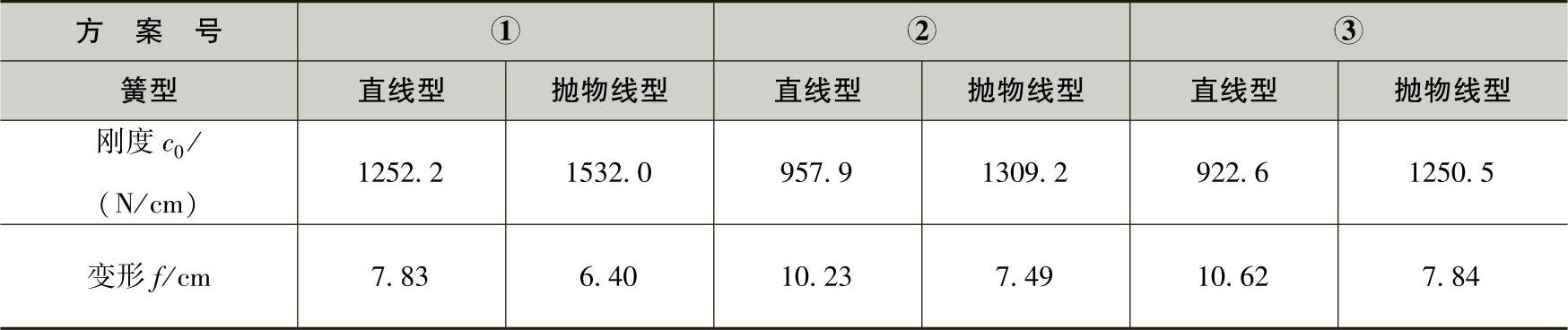
由表3-29数据可知,只有方案②、③的直线型弹簧能满足总成静挠度10cm的要求。
5)计算总成应力。
总成应力σA实际是各片根部应力的平均值,它可由式(3-113)计算。夹紧距离S取为10cm,并认定一端的有效长度点为最大弯矩点,即
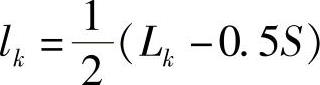
计算结果见表3-30。
表3-30 总成应力

由表3-30数据可知,仅方案②能够满足总成应力的要求,但方案②中的抛物线型总成变形又太小。所以,方案②直线型为最终选定方案。下面的计算仅涉及选定方案。
6)计算单片应力。
单片应力σkx可用式(3-114)计算。计算断面参见各片计算断面图(图3-49)。计算结果见表3-31,单片应力图如图3-50所示。
表3-31 单片应力
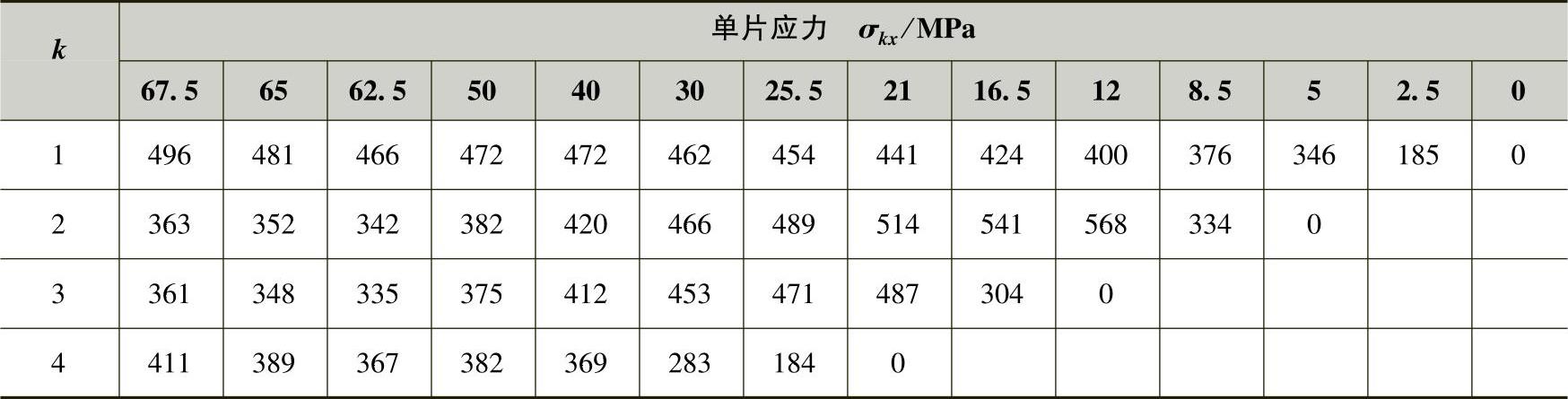
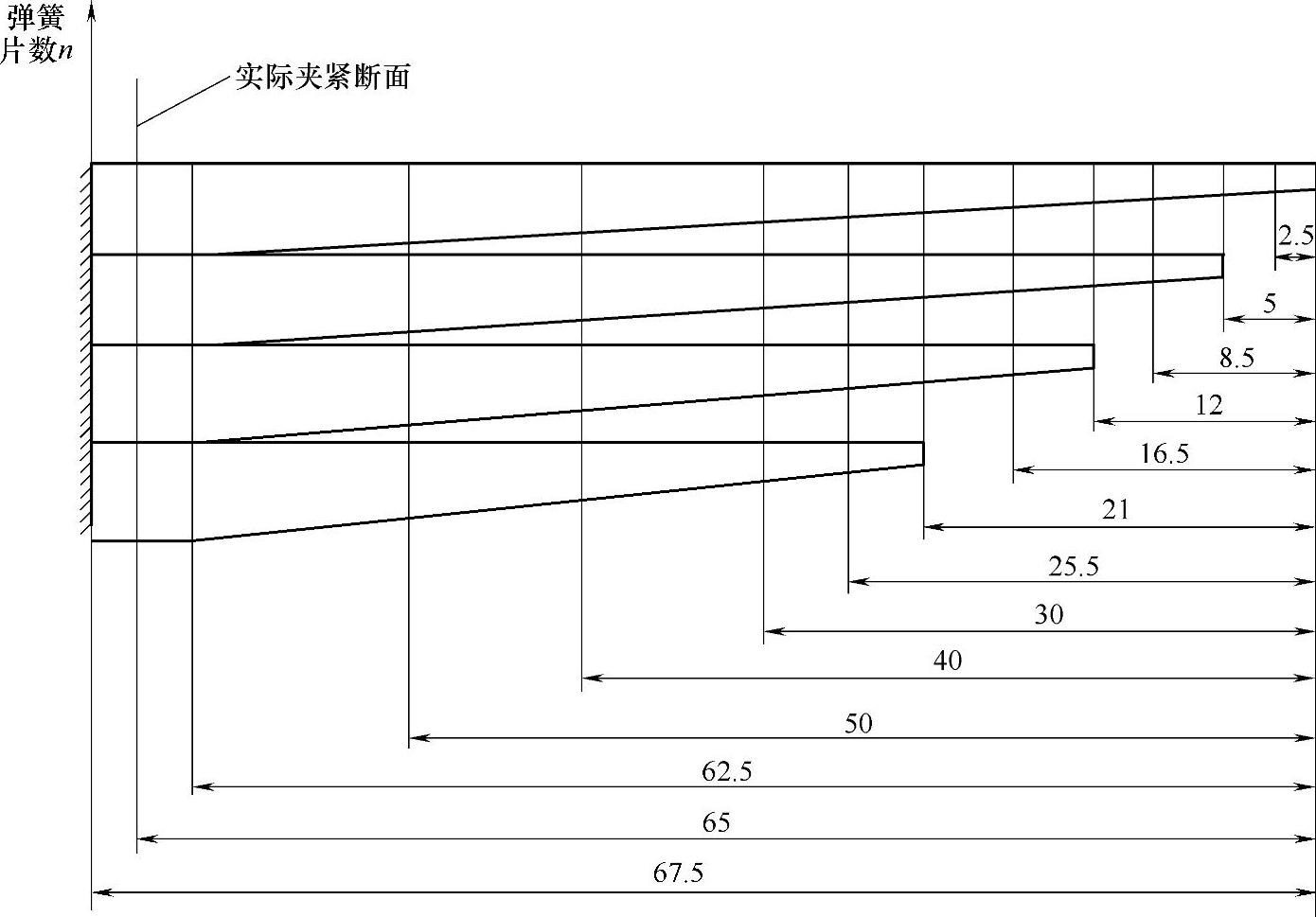
图3-49 各片计算断面图
由单片应力表和单片应力分布图可知,第2片的应力在第3片端点l3处为568MPa,这是全簧的最高应力,它已接近总成应力的1.5倍。在实际设计中,对此种情况,应适当调整结构参数,以使应力在全簧和在各片中分布合理。须知,总成应力不能说明应力的分布状况。
从单片应力的计算结果可知,相对当今合金钢材的许用应力还是较小的。因此实际设计板簧时,完全可以增大总成变形,适当放大单片应力。
由于选定的示例方案②不仅为直线型,而且各簧片的长度也不相等。除末片外,其余各片均受有两个集中载荷。因此,单片应力的分布,就远离了等强度规律。不过,它较之等断面簧的图3-41所示的应力分布,还是要均匀得多。
7)确定单片曲率半径。
要确定各单片的自由曲率半径,必须先确定各片的预弯矩,并计算非单一圆弧系数。
①确定各片预弯矩。主片预弯矩M01用式(3-120)计算,其余各片的预弯矩M0k按图3-48分配。计算和分配的结果见表3-32。
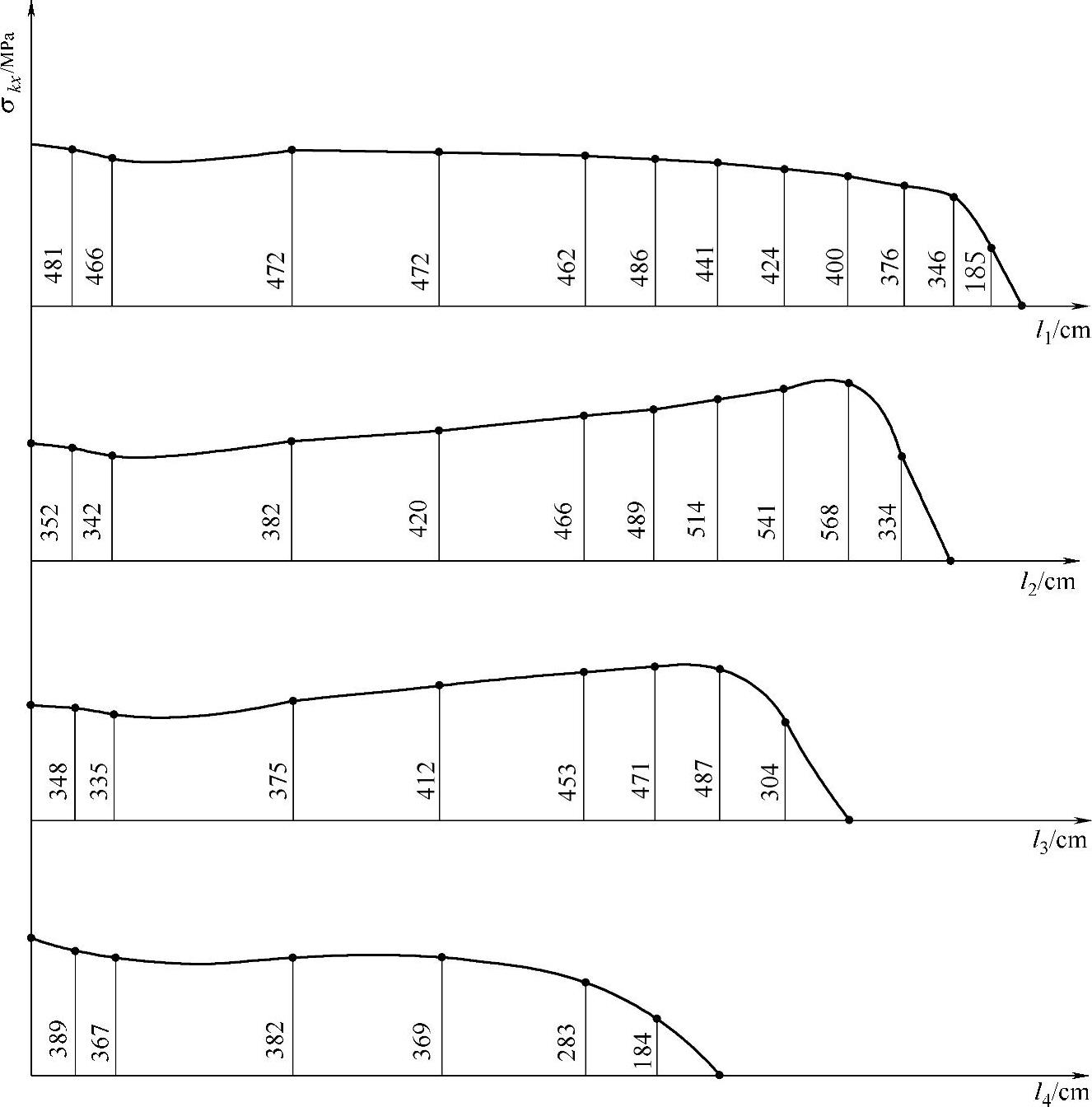
图3-50 单片应力分布图
表3-32 各片预弯矩

②计算非单一圆弧系数。非单一圆弧系数α按式(3-124)计算,式中的片间支垫厚度δi均取为0.3cm。为了掌握ΔHk的计算方法,故将计算程式与计算结果,一并列入非单一圆弧系数的计算表(表3-33)之中。
③计算各片曲率半径。各片自由曲率半径Rk可借用非单一圆弧系数的计算表中的数据利用式(3-122)计算。计算结果见表3-34。
表3-33 非单一圆弧系数的计算
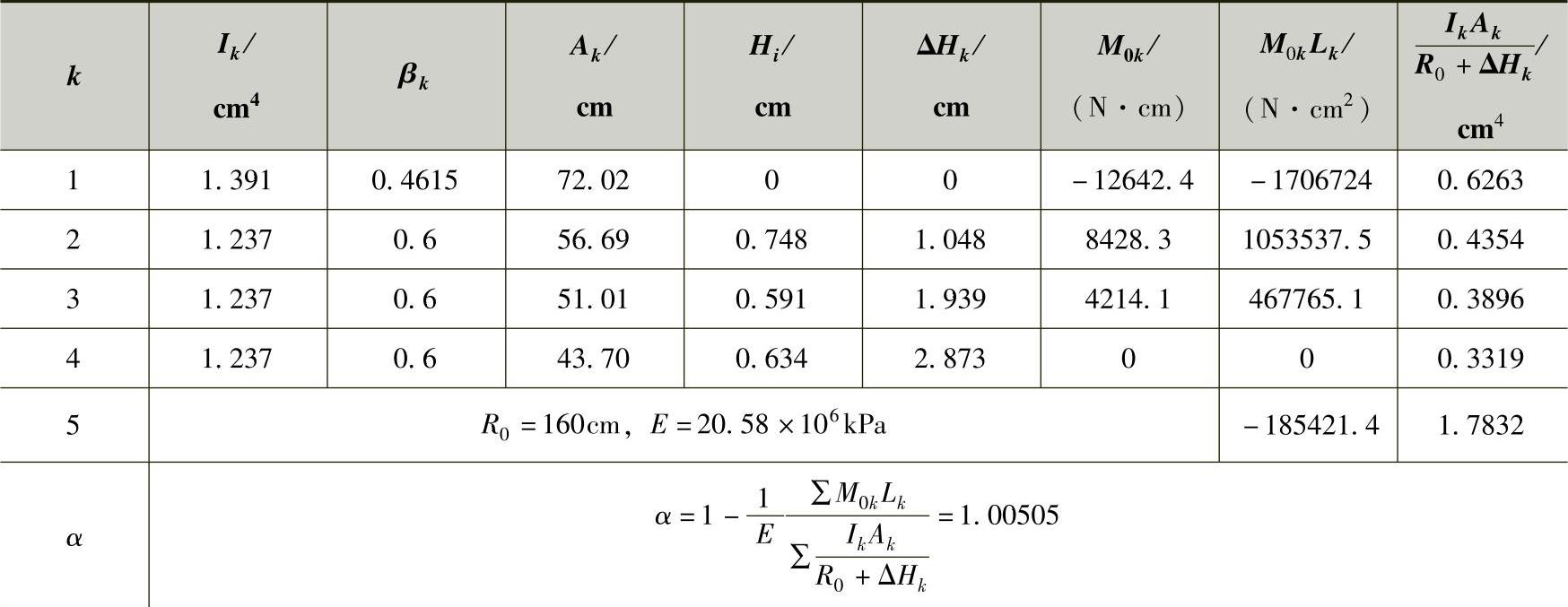
表3-34 各片曲率半径

注意:圆整时末片的曲率半径只能减小,不能增大,因为增大就不能与上一片保持接触。
8)验算总成曲率半径。
总成曲率半径R0可用式(3-122)或式(3-123)进行验算,验算程式及其结果一并列入总成曲率半径的验算表(表3-35)中。
表3-35 总成曲率半径的验算表

表3-35的数据说明,R0的计算结果和设计要求是一致的,各单片自由曲率半径选定正确。此外,式(3-122)和式(3-123)计算结果的一致性,又说明了非单一圆弧的假设是有根据的。
9)验算各片预弯矩。
各片预弯矩可用式(3-127)验算:

式中的代号与式(3-122)相同。不过非单一圆弧系数α则应由式(3-125)计算。
由式(3-127)计算的预弯矩值见表3-36。
表3-36 各片预弯矩的验算结果

由表3-36的数据可知,对于各片预弯矩之和∑M0k,若考虑非单一圆弧影响,则基本归零;若不考虑,则不能归零。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







