普通钢板弹簧也就是各片片宽相等、单片片厚不变的对称钢板弹簧,它是一种最为基本的而且使用最为广泛的弹性元件。钢板弹簧的设计,是刚度、应力和弧高的统一,是一件十分复杂的工作。它必须具体考虑如下一系列的问题。
1.片端力
片端力是计算单片应力和总成刚度的基础,而单片应力又是强度和寿命的依据。计算单片应力有共同曲率法和集中载荷法两种方法。共同曲率法的基本假设是片间全部接触并具有共同的曲率,而集中载荷法的基本假设是片间完全分开,载荷只在片端传递。本书只考虑集中载荷法,因为它更加接近实际,特别是装有片间支垫的情况。
为得到各片间端部接触点的片端力,先假定在已知弹簧载荷及受力状况的情况下,求其每种状况每一单片的变形,参见表3-4。表中列有4种受力状况,即力作用于端部,求中部某断面的变形;力作用于中部,求相应断面的变形;力作用于端部,求端部处的变形;力作用于中部,求端部的变形。表中还列有四种变形:fAk为力作用于lk片端部,中部某断面的变形;fBk为力作用于lk片中部,相应断面变形;fCk为力作用于lk+1片端部,端部处的变形;fDk为力作用于lk+1片中部,端部处变形。
表3-4 四种工况下的单片变形

(续)
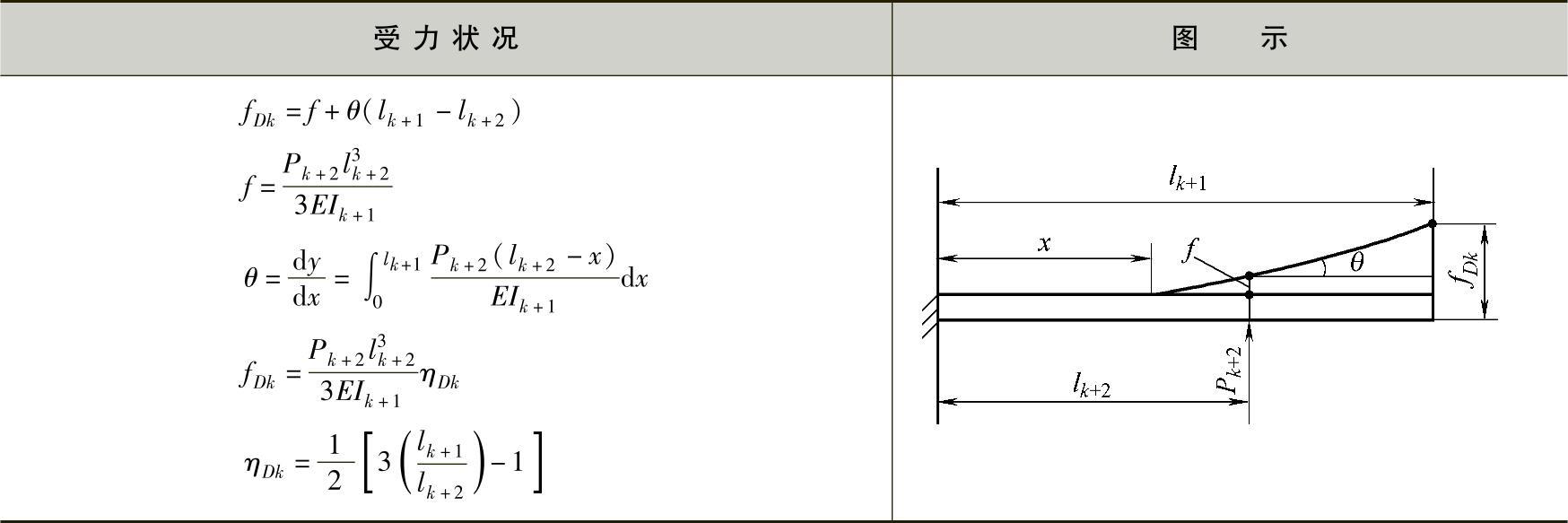
有了上述四种受力工况下的变形,再根据相邻片间接触点的变形相等的条件,就可建立整副弹簧的平衡方程为

即
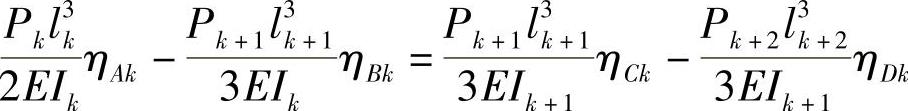
经变换可得

这是一个含有(n-1)个方程的线性方程组,其特点是每一个方程式不多于三个未知数,同时相邻下一个方程式只增加一个新的未知数,因此方程组不必采用行列式原理就可解出。
方程组的具体解法:一般是从最后一个方程开始倒过来求解,逐一类推,直至将第一个方程变为只含P1和P2的方程,由于P1为已知,故全部片端力得解。
为计算方便,也可按连分式法直接求解
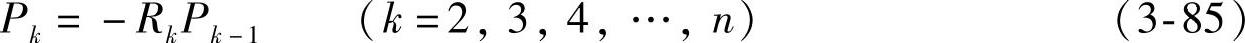
式中 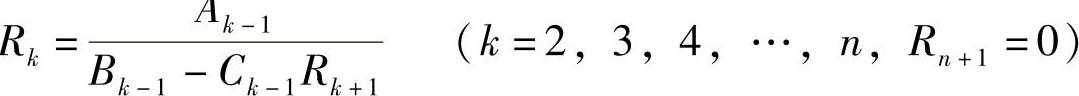 ;
;
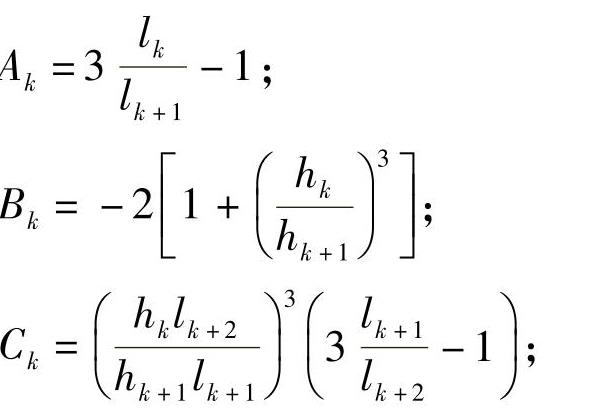
lk——各片减去夹紧长度之后的一半,ln+1=0。
片端力还可表示为下列形式
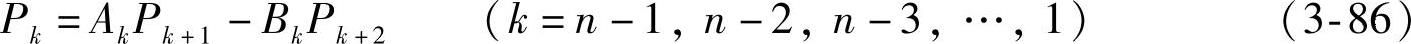
式中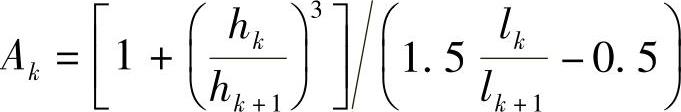 ;
;
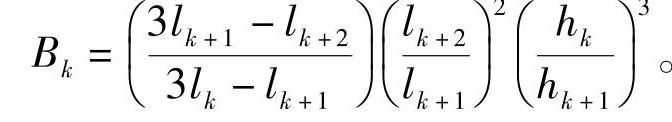
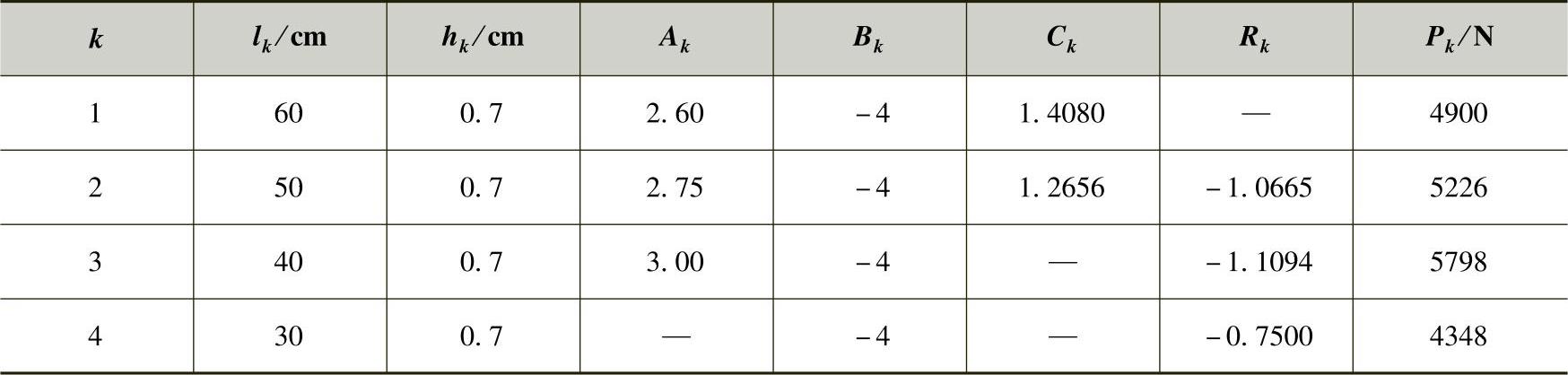
【片端力计算示例】
采用式(3-85)计算。示例弹簧参数:n=4,夹紧后的一端长度为lk,片厚hk,主片片端载荷为P1。这些参数,以及计算过程中的参数Ak、Bk、Ck、Rk和计算结果Pk均列于表3-5之中。
表3-5 片端力示例计算
2.变形及刚度
(1)弹簧变形
弹簧总成端部的变形,对于对称簧来说,就是弹簧总成的变形。有了弹簧在非夹紧状态下的总成变形,就可以计算弹簧总成的自由刚度和夹紧刚度了。下面是推求整副弹簧在满载载荷P的作用下端部的变形,如图3-35所示。

图3-35 弹簧总成的变形
根据莫尔定理,弹簧端部在力P作用下的变形为
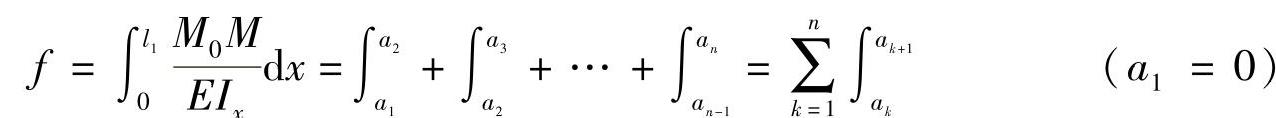
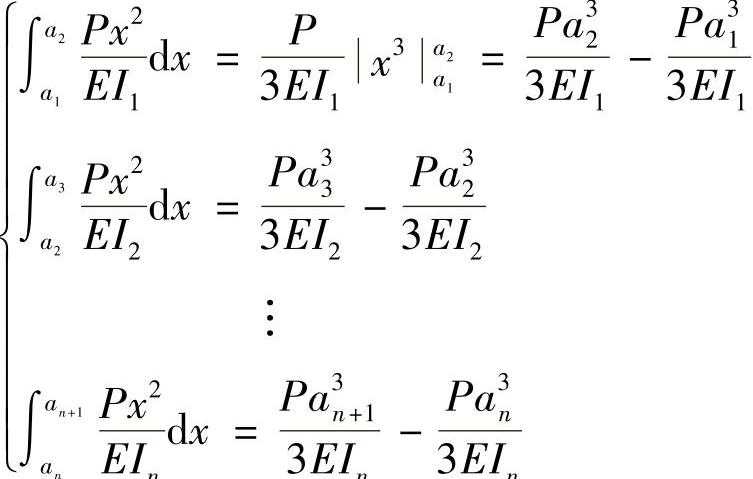
进而可得
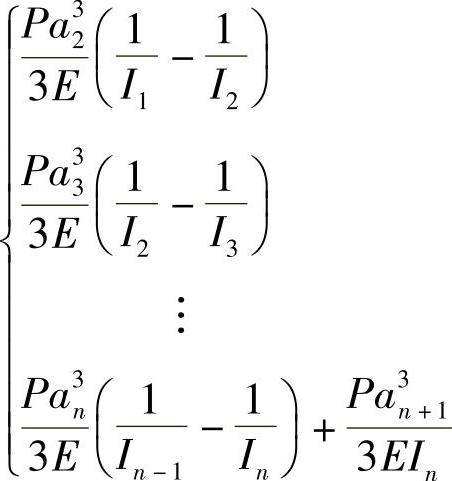
于是,弹簧一端的变形量为
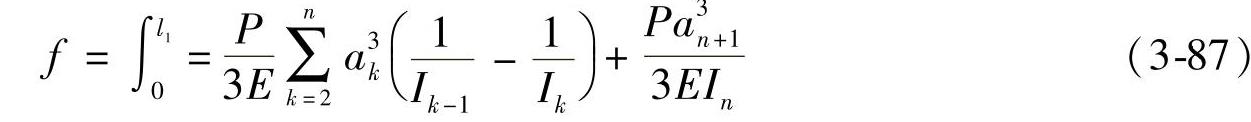
为计算方便,还可表达为

(2)总成自由刚度
由式(3-88)可知,整副弹簧的自由刚度为

式中 α——修正系数,可取α=0.90~0.92;
ak=l1-lk,an+1=l1;
Ik——惯性矩,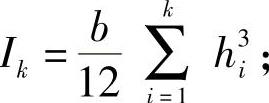
b——弹簧片宽。
(3)总成夹紧刚度
为计算需要,自由刚度c0还须转换为夹紧刚度cJ。夹紧有刚性夹紧和弹性夹紧之分,一般刚性夹紧计算式为

式中 S——夹紧长度;
L——主片伸直长度。
夹紧刚度也可用减去夹紧长度之半的长度进行直接求变形得到。
为提高材料利用率,增大材料的有效部分,也可采用斜置夹紧。其中,板簧上置式,夹紧螺栓上窄下宽;板簧下置式,夹紧螺栓上宽下窄。
【计算示例】
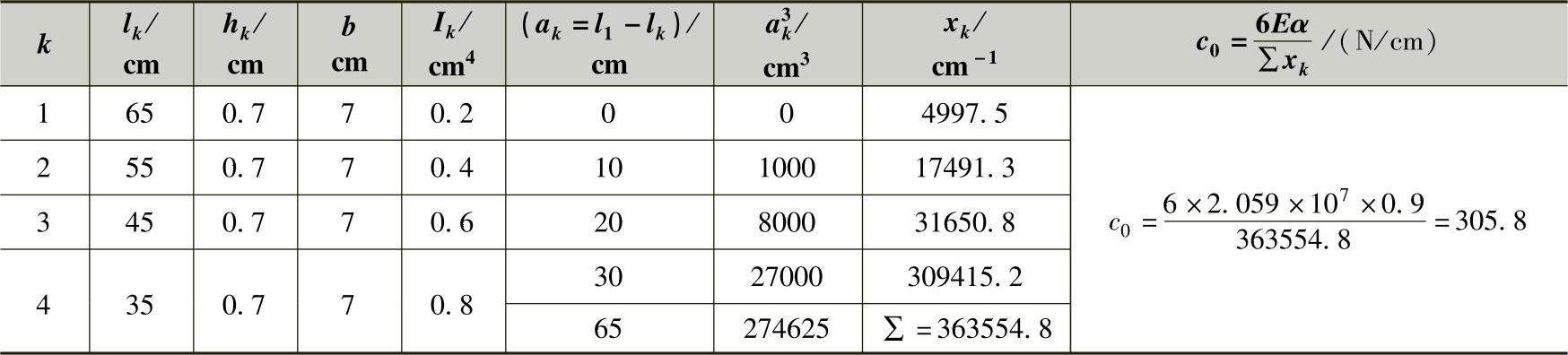
①以表格的方式,利用式(3-89)先计算自由刚度c0。
②再利用式(3-90)计算夹紧刚度cJ为
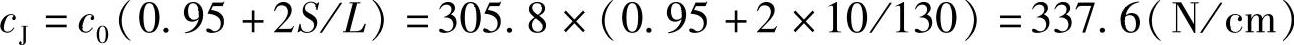
表3-6 自由刚度的计算
3.曲率半径及预应力
钢板弹簧曲率半径的设计计算有两个任务:一是在已知各片长度Lk(全长为大写L,计算时一般为半长,用l表示)、宽度b、厚度hk以及曲率半径Rk的情况下,计算总成(主片)在自由状态下的曲率半径R0,同时校核各片的预应力δ0k;二是在已知总成曲率半径、各片长度、宽度、厚度的情况下,确定各片的预应力及曲率半径。下面具体谈谈这两个方面的问题。
(1)总成曲率半径的计算及各片预应力的校核
1)总成曲率半径的定义。
钢板弹簧总成在自由状态下的曲率半径是指主片上的曲率半径。由于装配后的主片是由若干个不同的圆弧所排成的(图3-36),所谓总成曲率半径只不过是总成自由弧高H0的换算半径,即
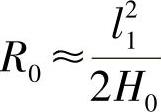
式中 l1——主片长度之半;
H0——主片上面中心点至中点连线的距离。
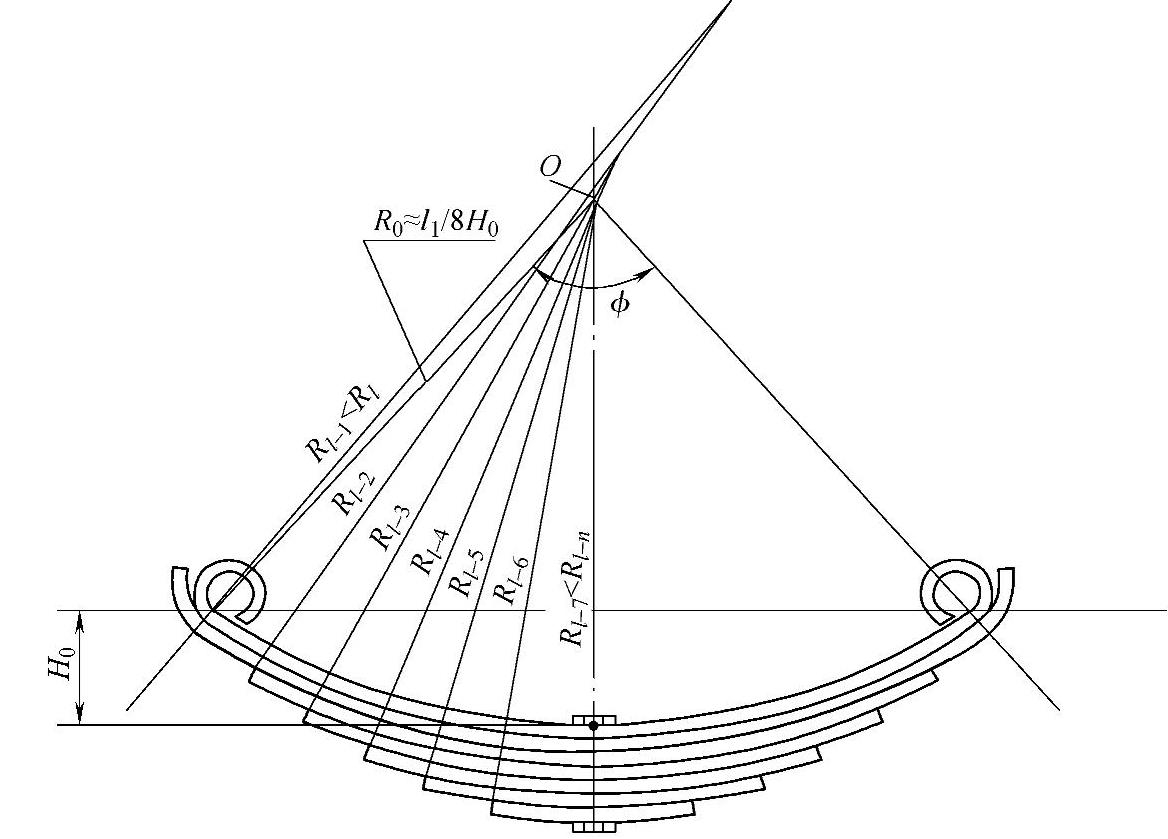
图3-36 主片曲率的构成
主片长度L1范围内的两端由主片两端终点向主片换算曲率中心O所引的两条线段,便认为是总成(主片)曲率半径。两线段之间的夹角为
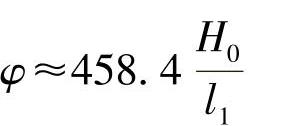
即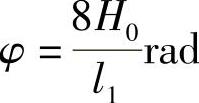
随着卷耳形式的不同,自由弧高也不一样(图3-37{。
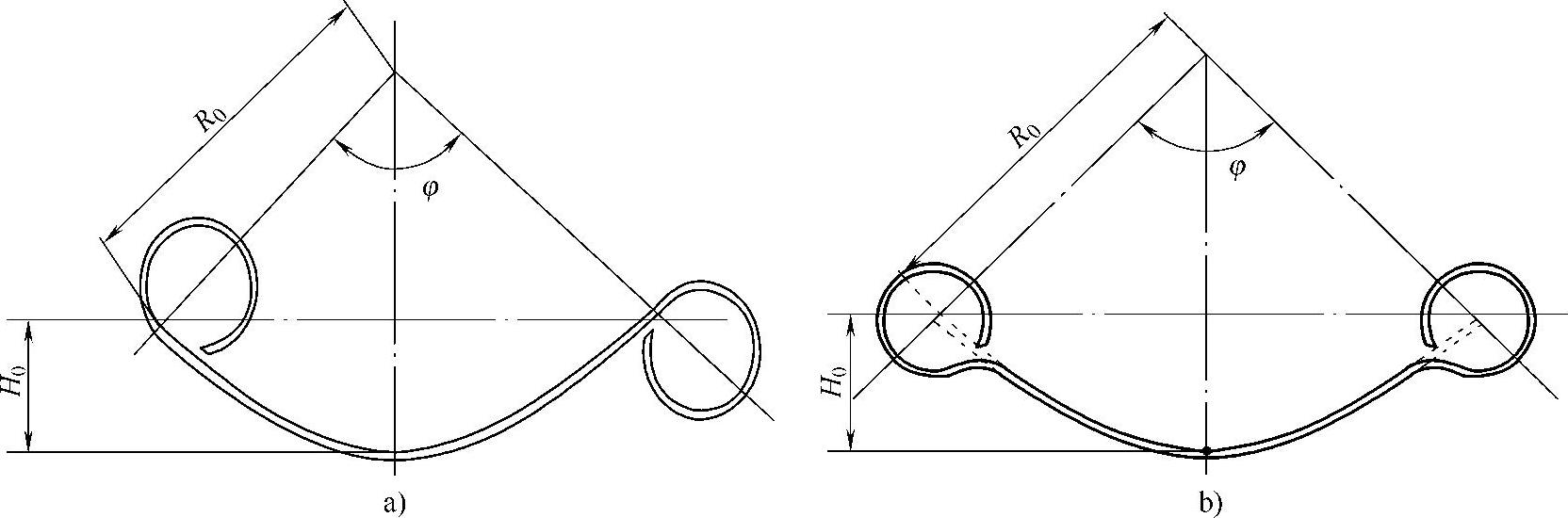
图3-37 总成自由弧高的定义
2)计算总成曲率半径主要方法述评(注意:弹簧半长用l表示,全长用L表示)。
国内普遍采用的计算钢板弹簧总成弧高和曲率半径的方法有如下几种:
①帕尔希洛夫斯基将各片弹簧由上至下依次装配,从而得出了一种计算方法。简称为“帕氏逐装法”,其总成自由弧高的计算公式为
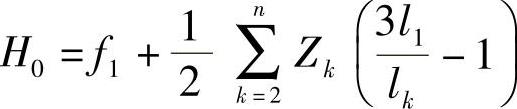
式中 k——各片序号;
n——总片数;
lk——各片长度之半,其计算式为
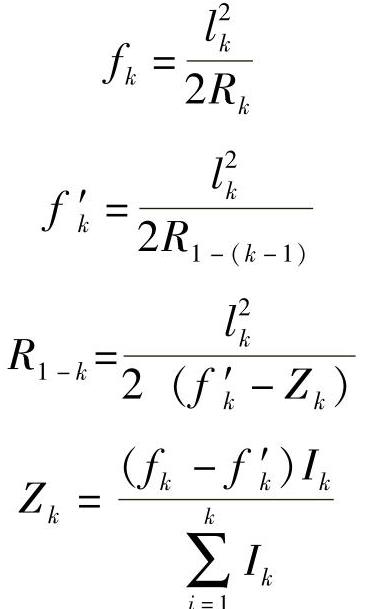
式中 Ik——各片之惯性矩。
帕氏还根据中心螺栓拧紧时作用于每一叶片上的力矩之和为零的思想,即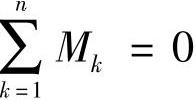 ,得出了一种方法,简称为“帕氏M法”。其总成半径的表达式为
,得出了一种方法,简称为“帕氏M法”。其总成半径的表达式为

②郭孔辉院士依据装配后各叶片产生的势能Uk之和为最小的原理,即 而导出的计算方法,简称为“郭氏U法”,其计算公式为
而导出的计算方法,简称为“郭氏U法”,其计算公式为
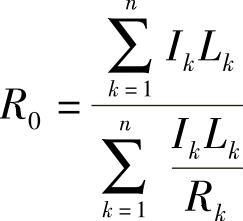
③内蒙古工学院杨宗孟教授指出:距中心螺栓中心线三分之一主片长度之半(l1/3)处的主片曲率半径,便可视为总成曲率半径,此法简称为“杨氏(l1/3)处法”。其计算公式为
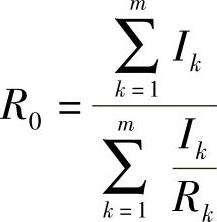
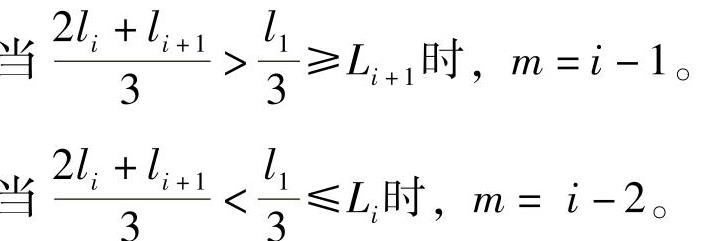
i为各片序号,由下式判定(图3-38):


图3-38 杨氏(l1/3处{法
为研究上述各种方法的可行性及其相互间的关系,任意选取了10副板簧,并用各种方法对其进行计算。这些弹簧的参数及其计算结果列入表3-7~表3-9之中。
表3-7 弹簧参数表
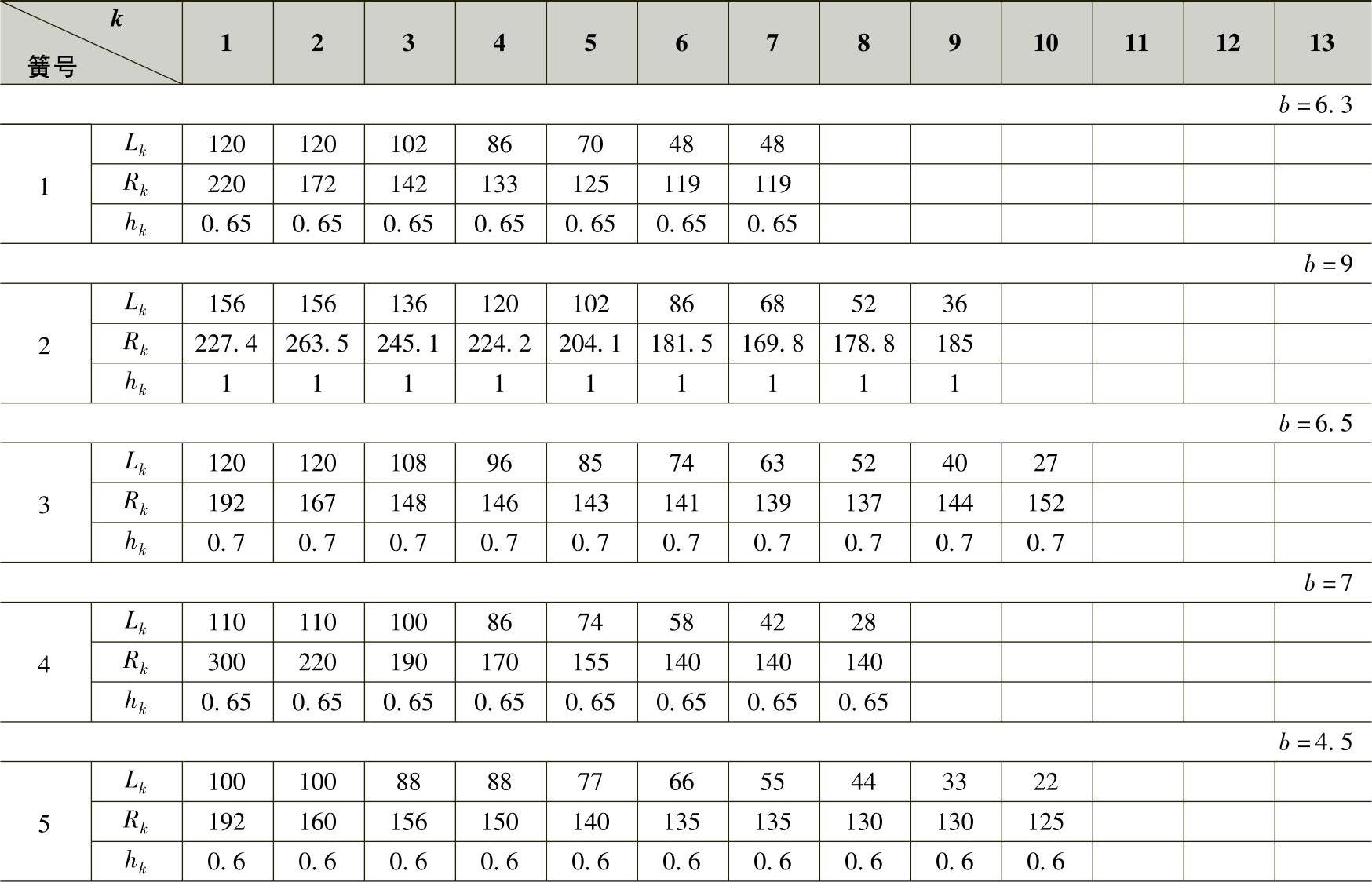
(续)

表3-8 按不同方法计算的10副弹簧的总成曲率半径值 (单位:cm)
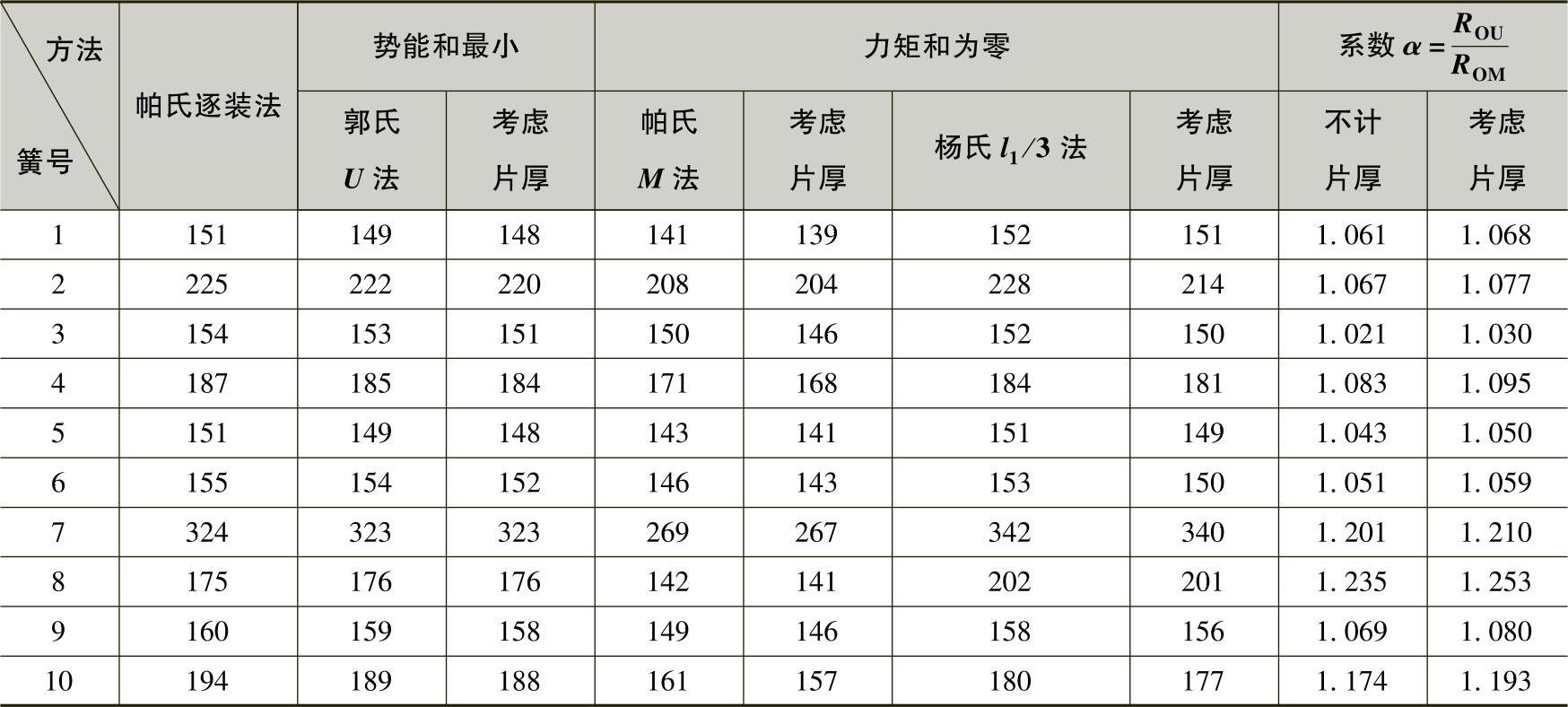
表3-9 按“帕氏逐装”法计算的10副弹簧的主片分段曲率半径值 (单位:cm)

通过分析,结合观察计算结果归纳可知,各种方法从原理上看,无外乎产生于势能和最小以及力矩和为零的思想。
“郭氏U法”的依据是最小势能原理,它反映了问题的本质。这个从力学概念所建立的计算公式,还可以从数学的角度直接得到。按照加权统计的方法,只要把某一片的惯性矩与长度之积IkLk同各片积之和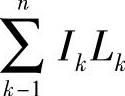 之比
之比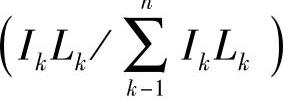 看作某一片的曲率
看作某一片的曲率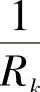 的权,那么,其加权
的权,那么,其加权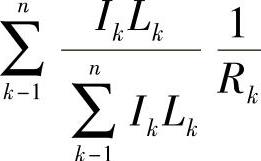 便是总成的曲率了,即
便是总成的曲率了,即

这就从另一角度证明了“郭氏U法”的可靠性。事实上,“郭氏U法”所得公式的计算结果也是较为接近实际的。
“帕氏逐装法”表面上看是一种几何关系,但挠度的变化就隐含着能量变化的实质。虽然计算起来需要依次倒换,比较麻烦,但计算结果较为准确,一般略大于“郭氏U法”的计算结果。采用两种方法计算的10副板簧的R0的差值见表3-10。
表3-10 两方法计算10副板簧的R0的差值

“帕氏逐装法”还能将装配到第k片时的主片局部曲率半径Rl-k全部计算出来,见表3-9和图3-36。
“帕氏M法”仅是“郭氏U法”的一个特例,即忽略了各片长度的影响,因而所得出的公式不能付诸实用。
由表3-9可知:根据“帕氏逐装法”,当装完第n片之后,主片上第n片长度范围之内的曲率半径Rl-n,就是“帕氏M法”公式所计算的结果,如图3-36所示。
“杨氏l1/3处法”计算最为简单,但计算公式仍是“帕氏M法”公式,不同的只是少算几片而已。各片长度的影响同样被忽略。
此法的计算结果总可在“帕氏逐装法”计算表的Rl-k栏中找到,参见表3-9。由于Rl-k值呈现台阶式的变化,因而,R0值随着多算或少算1片也在进行台阶式的变化。
与“郭氏U法”比较,10副板簧计算结果的偏差值见表3-11。
表3-11 10副板簧计算结果的偏差值

从表3-11数据可知:对于各片等厚时,偏差尚小;而各片不等厚时,却有着不可忽视的偏差。
此处,有两个问题值得研究:一个是多算或少算1片,取决于l1/3的位置;而算多少片,还取决于(li-li+1{值,当li和li+1出现微小变化时,就有可能带来计算结果一个台阶式的变化。按照能量变化的观点,这是不可能的!另一个是有的弹簧,如10副弹簧中的8号和10号,其计算结果与“帕氏逐装法”的计算结果比较错开了一个台阶,请参见表3-8和表3-9。这就远远不是修正所能解决问题的了。所以,采用“杨氏l1/3处法”计算不等厚弹簧时应持慎重态度。
上述各种方法,均因片厚与其曲率半径的比值很小,而未考虑片厚。不考虑片厚一般使曲率半径只增大约1%,其绝对值也未超过5cm,对总成弧高的影响更是微乎其微。然而,从应力的角度来看,这一微小变化,各片特别是主片预应力却将产生不可忽视的计算误差。
“帕氏M法”“郭氏U法”等方法,在推导计算公式时,都假设各片在组装后,具有单一的曲率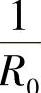 。这个
。这个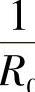 除了忽视片厚的影响外,还忽视了非单一圆弧这个客观存在。按照单一圆弧的假设,各片的弯矩及预应力采用下列两式进行计算
除了忽视片厚的影响外,还忽视了非单一圆弧这个客观存在。按照单一圆弧的假设,各片的弯矩及预应力采用下列两式进行计算
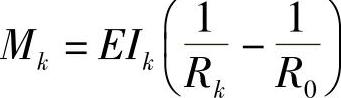
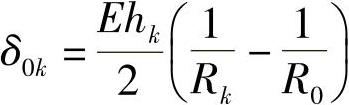
这是钢板弹簧计算中的两个基础公式。由此可见,基础公式有了偏差,推导的结果就难免有偏差。
“帕氏M法”公式计算的结果之所以大幅度地偏离实际值,正是将弯矩公式代人 的公式之后、把各片的误差叠加起来的结果。
的公式之后、把各片的误差叠加起来的结果。
“郭氏U法”在推导R0的计算公式时,同样也带入了弯矩公式,但误差并不明显,计算结果较为接近实际。
如何具体建立弹簧的计算过程呢?下面将研究这个问题。
3)总成曲率半径的计算。
①按最小势能原理推导总成曲率半径的计算公式。
在已知总片数n、各片长度Lk、惯性矩Ik,自南状态下的曲率半径Rk的情况下,考虑片厚影响,但仍假设组装后各片保持单一圆弧,因按最小势能原理推导公式,这一假定影响不大。因此,组装后各片的曲率变化量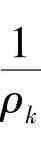 与弯矩Mk可分别表示为
与弯矩Mk可分别表示为
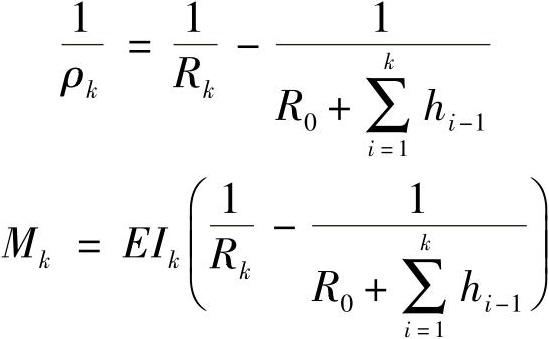
即
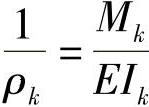
按照单一网弧的假定,故组装后作用于各片的弯矩仅是一个力偶矩,凶此第五片的势能为
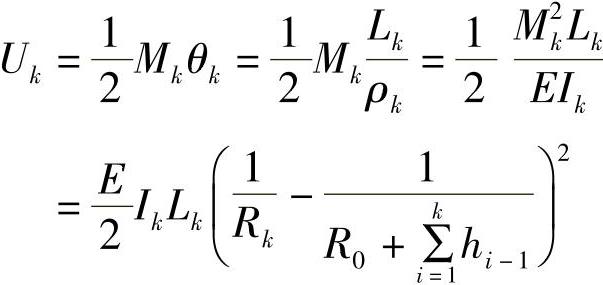
其总成的合势能U为
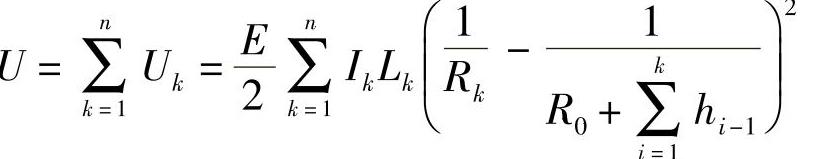
而总成的合势能U对R0的一阶导数为
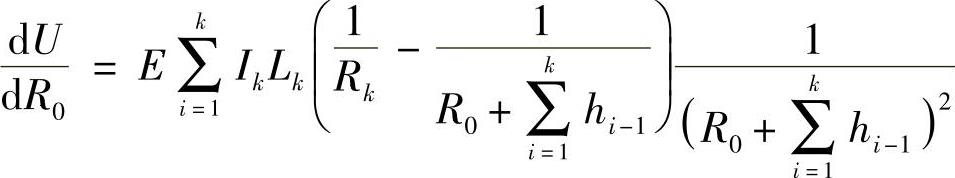
按照最小势能原理,当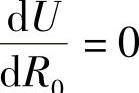 时,总成处于稳定状态。也就是说,此时的R0值,便是总成的曲率半径。据此,令前式为零,便可解得
时,总成处于稳定状态。也就是说,此时的R0值,便是总成的曲率半径。据此,令前式为零,便可解得
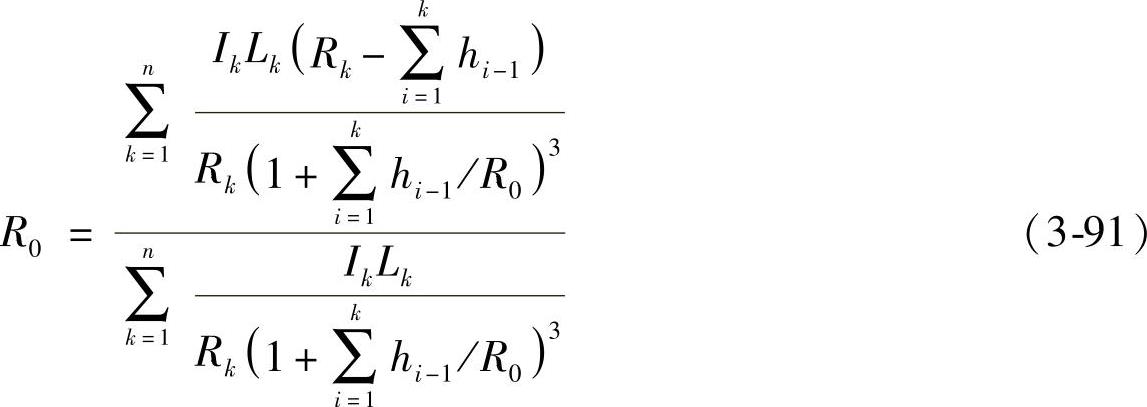
若令式(3-91)中的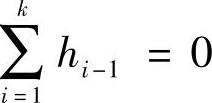 ,便立即得到“郭氏U法”公式。式(3-91)右端含有R0,这似乎无法计算,但可先以
,便立即得到“郭氏U法”公式。式(3-91)右端含有R0,这似乎无法计算,但可先以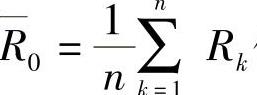 代替进行初算,然后再以所得的结果带入计算,逐次逼近,直至获得令人满意的结果。事实上,由于
代替进行初算,然后再以所得的结果带入计算,逐次逼近,直至获得令人满意的结果。事实上,由于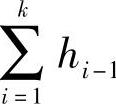 相对于R0值很小,故一次计算就能获得令人满意的结果。
相对于R0值很小,故一次计算就能获得令人满意的结果。
为方便计算,令
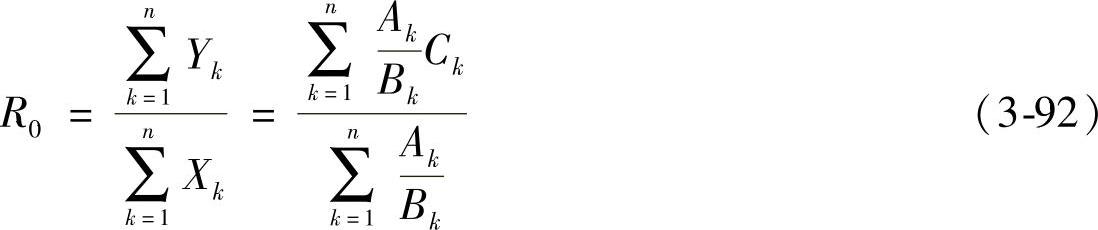
当各片不等厚时,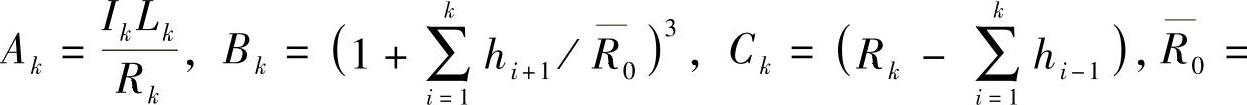
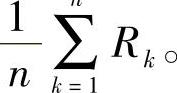
当各片等厚时,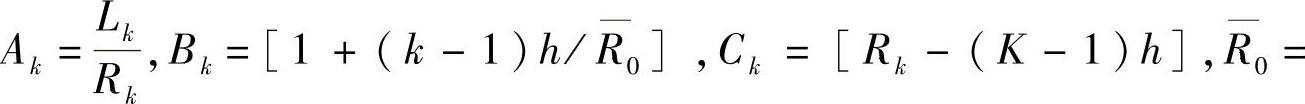
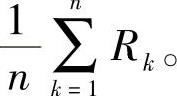
下面以1号簧为例,列出计算程式,其计算结果见表3-12。
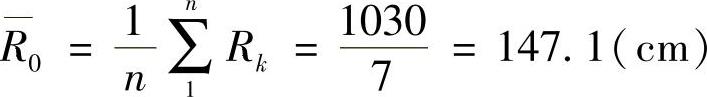 (https://www.daowen.com)
(https://www.daowen.com)
表3-12 按最小势能原理计算R0
②按力矩和为零的思想推导总成曲率半径的计算公式。
若已知片数n,各片惯性矩Ik,自由状态下各片的曲率半径Rk,并考虑片厚的影响,再假定组装后各片具有一个换算的(当量的)单一圆弧。因此,组装后各片的曲率改变量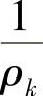 与弯矩Mk分别表示为
与弯矩Mk分别表示为
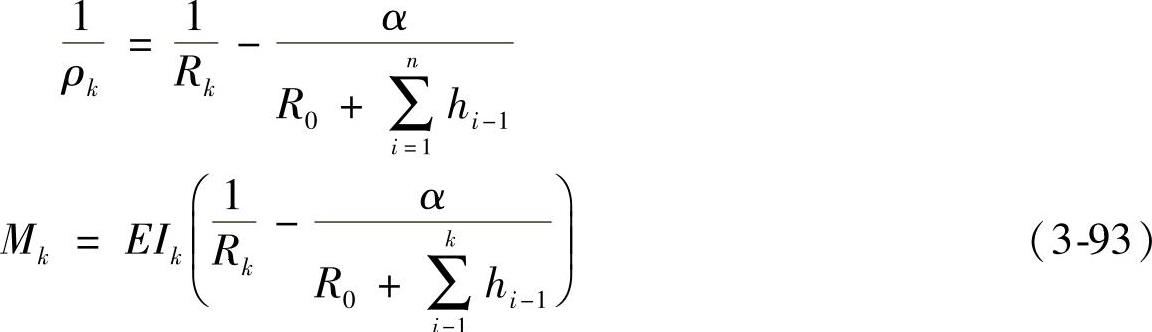
式中 α——曲率变化系数或非单一圆弧系数。
在上述假定的基础上,再根据预应力δ0k的合力矩Mk为零的思想可以得到
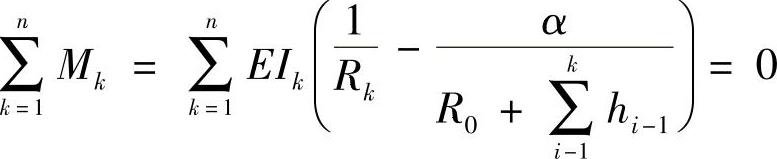
解上式可得
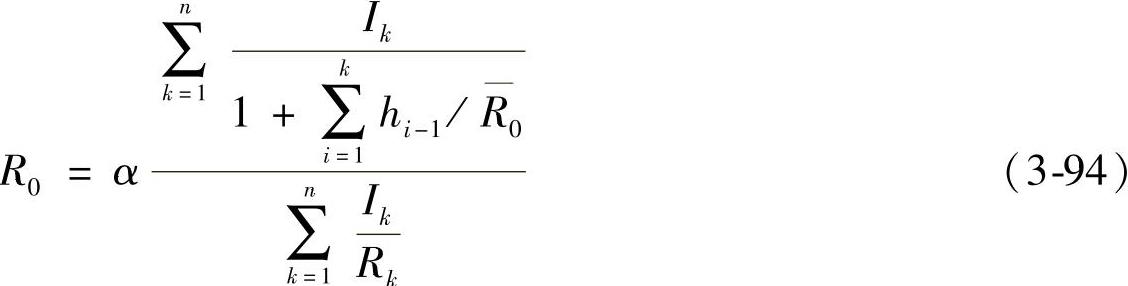
式中
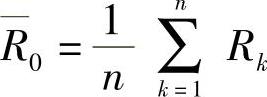
为便于计算,将式(3-94)变为

当各片不等厚时,有
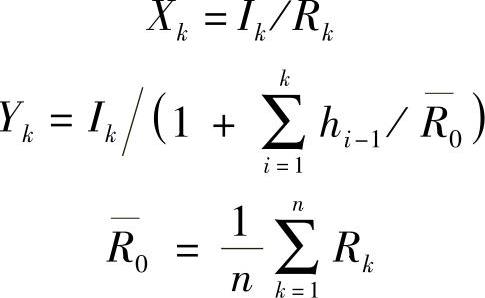
当各片等厚时,有
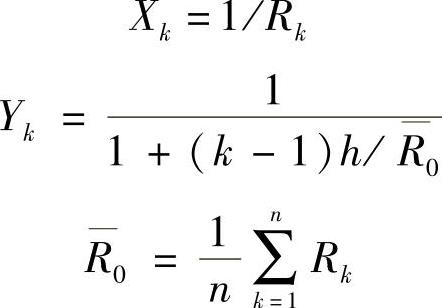
观察式(3-94)和式(3-95)可知,各片的非单一圆弧系数α,已成了总成的非单一圆弧系数(修正系数)了。因为当曲率变化量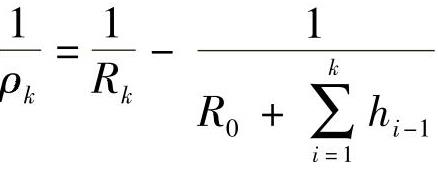 时推导出的R0的计算公式,正好是α=1时的形式。
时推导出的R0的计算公式,正好是α=1时的形式。
③非单一圆弧系数α的确定。
要使式(3-95)付诸实用,必须确定α值。那么又如何确定呢?既然α叫做非单一圆弧系数,那也就是说,它是考虑非单一圆弧情况下建立的公式所计算的结果与单一圆弧假设得出的公式所计算的结果的比值。换句话说,就是正确结果与单一圆弧假设的结果的比值。所谓正确结果,那也只是相对而言。此处,可以认定“帕氏逐装法”“郭氏U法”以及式(3-91)和式(3-92)计算的结果是相对接近实际的。所谓单一圆弧假设的结果是指“帕氏M法”所计算的结果,或者是式(3-94)和式(3-95)当α=1时的计算结果。请注意:“帕氏逐装法”中的R1-n,代表主片上在第n片长度范围内的单一圆弧的曲率半径。n片之后再也没有其他的片了,故可认定它是单一圆弧的。
因此,α便有下列三种表达和计算的方法。
“帕氏逐装法”的结果R0帕与R1-n之比,即

“郭氏U法”的结果R0U与“帕氏M法”的结果R0M之比,即
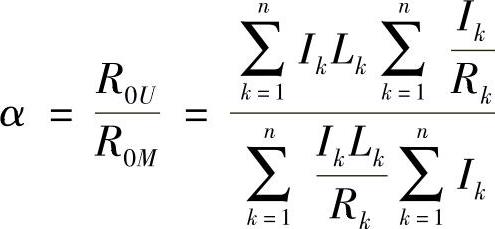
即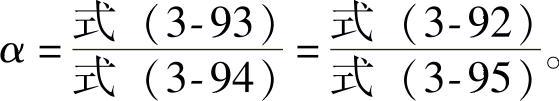
“郭氏U法”计算起来方便,但考虑片厚影响更为接近实际。
注意:计算α值的主要目的,不仅在于计算总成曲率半径,而更在于检验各片的弯矩和预应力。
下面以1号簧为例,先列出程式计算R0值,见表3-13。
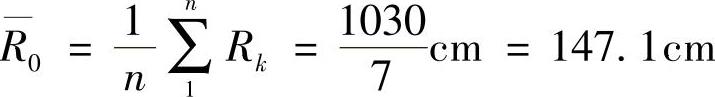
表3-13 按单一圆弧假设计算R0值
4)各片弯矩及预应力的校核。
钢板弹簧组装后,各片所承受的弯矩Mk可由式(3-94)计算,而各片中的预应力σ0k,则可由下式计算
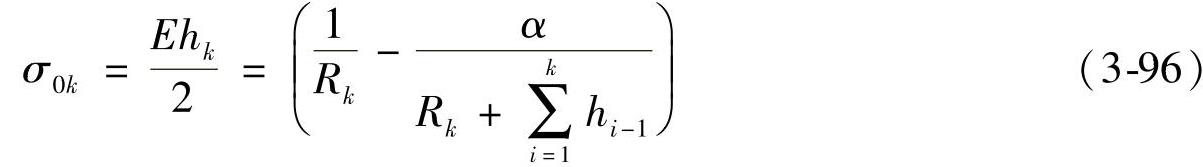
再计算α值为
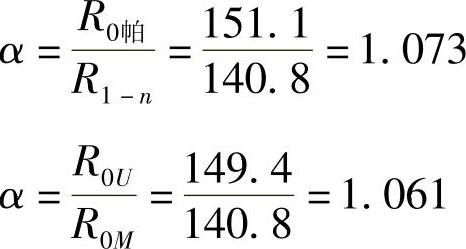
当取式(3-96)中α=1时,可计算得
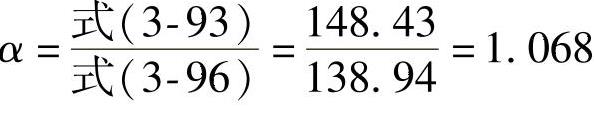
10副板簧计算的α值见表3-14。
表3-14 10副弹簧的α值

由表3-14中数据可知,三种方法计算的α值都较为接近。
在已知总成曲率半径R0,并知各片厚度hk、惯性矩Ik、曲率半径Rk的情况下,将上节方法求得的α值代入式(3-93)和式(3-96),就能校核各片的预应力和弯矩了。
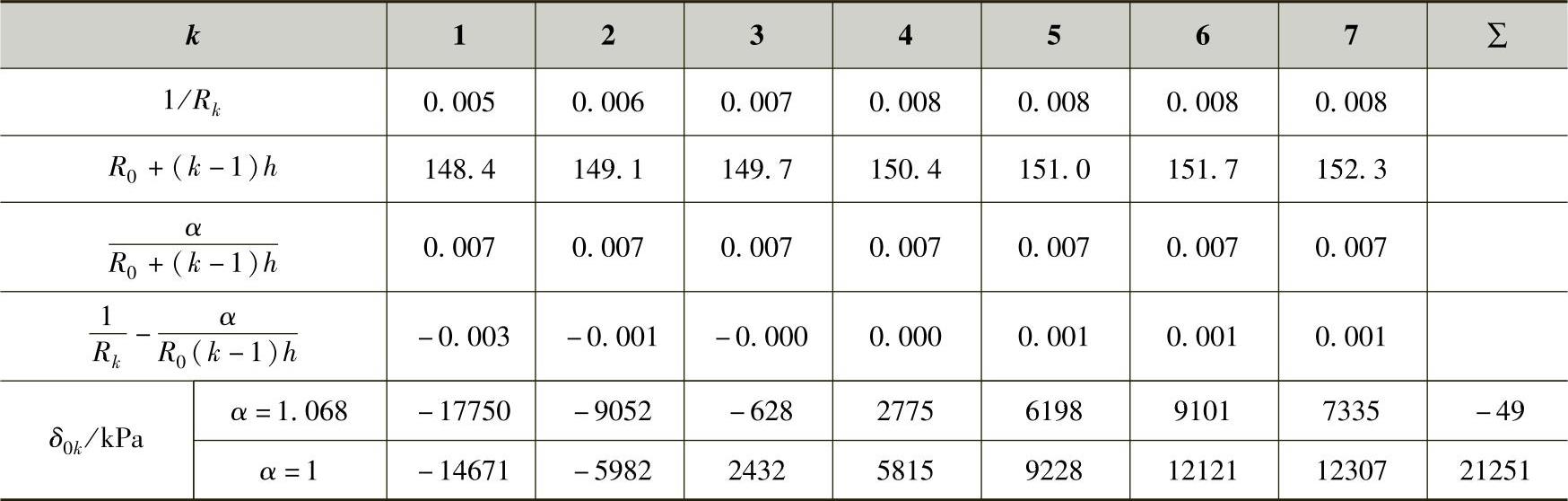
我们先以各片等厚的1号簧为例,按α=1和 来分别验算各片预应力的分布情况。其计算公式及结果见表3-15。
来分别验算各片预应力的分布情况。其计算公式及结果见表3-15。
表3-15 各片预应力的分布 Eh/2=682500
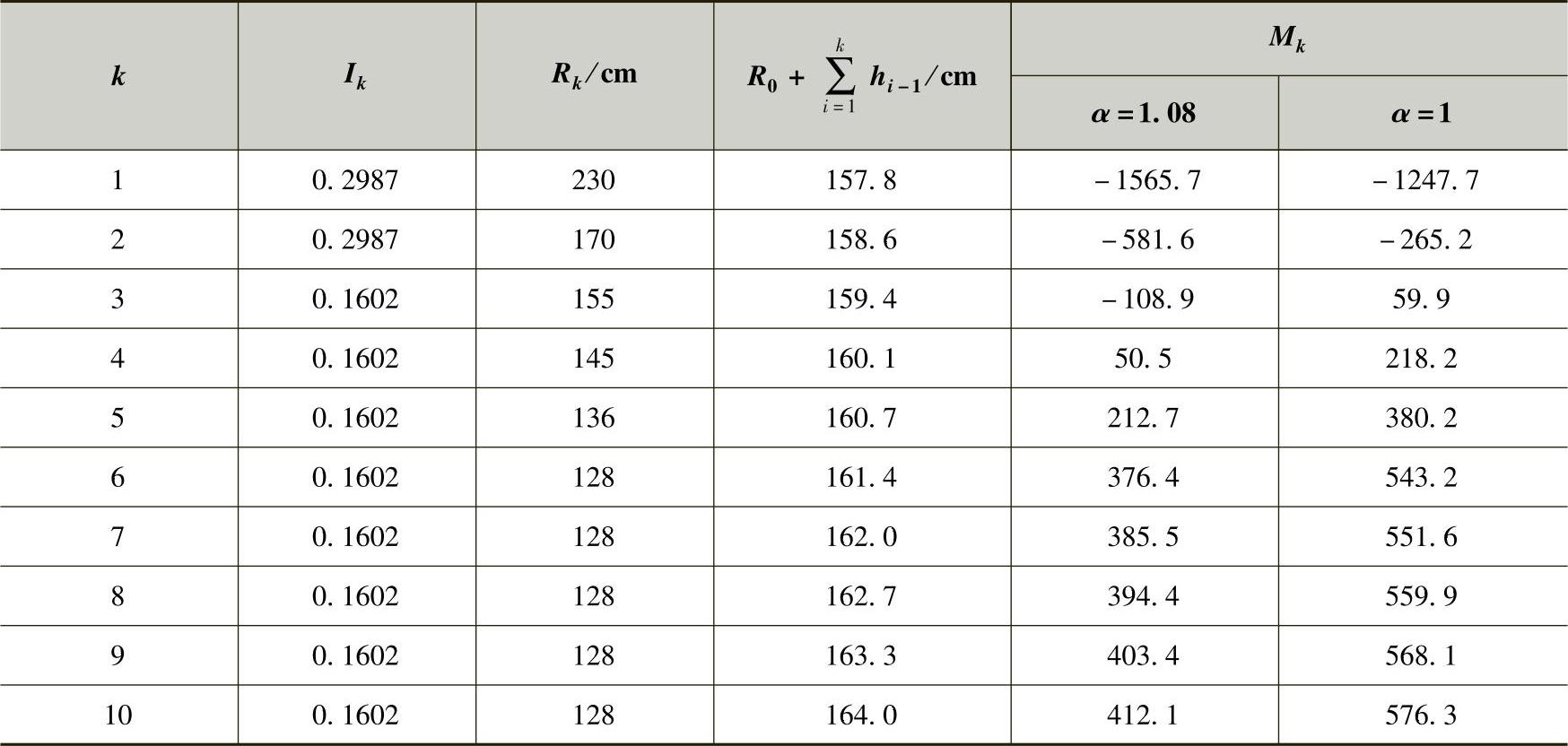
下面再以各片不等厚的9号簧为例,按所计算的α=1.08和α=1来分别计算各片的弯矩Mk的分布情况。其计算公式及结果见表3-16。
由于1号簧各片等厚,预应力之和应为零。而表3-16中数据当α=1.0684时,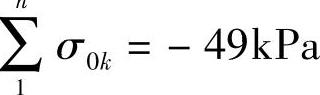 ,显然这只是计算误差问题。然而,当取α=1时,
,显然这只是计算误差问题。然而,当取α=1时,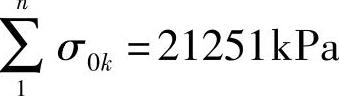 ,这是根本不符合实际的!9号簧弯矩的计算,也得到类似的结果。由此可见,采用非单一圆弧系数所计算的预应力和弯矩值是较为接近实际的。
,这是根本不符合实际的!9号簧弯矩的计算,也得到类似的结果。由此可见,采用非单一圆弧系数所计算的预应力和弯矩值是较为接近实际的。
表3-16 各片的弯矩值
(2)各片预应力和曲率半径的确定
问题(1)是对已有弹簧的验算,本问题是设计板簧中的重要环节,即在已经确定总成曲率半径R0、各片厚度hk、宽度b、长度Lk的情况下,确定各片的预应力σ0k和曲率半径Rk。
1)各片预应力的确定。
对于各片等厚的板簧来说,是确定预应力σ0k;对于各片不等厚的板簧来说,则是确定弯矩Mk。下面来研究确定各片弯矩的方法,因为这也包括了确定预应力的方法。
确定预应力,一般按参考文献[8]推荐的疲劳曲线图来选取。然而,计算说明,此法尚需进一步研究。
下面推荐一种确定各片弯矩和预应力的方法——弯矩曲线图法。图3-39就是所要推荐的弯矩曲线图。
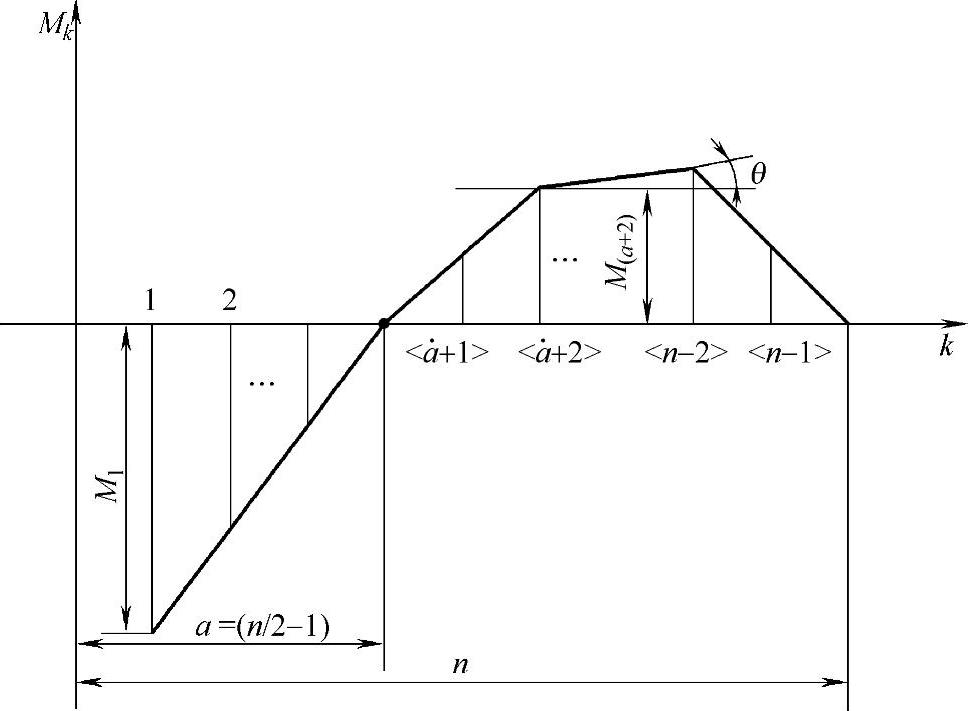
图3-39 弯矩曲线图
在图3-39中,纵坐标代表弯矩Mk,横坐标表示各片的序号k。当在横坐标上取一适当长度代表总片数n,并将其n等分,那么各等分点1、2……k……n便表示各片的位置。相应的纵坐标就代表各片预应力的弯矩。
图3-39中的M1、a、θ、M(a+2)是待求的未知参数,现分别加以确定。
①主片预应力的弯矩M1是为了保护主片而给定的负值弯矩,为
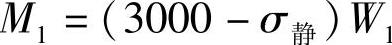
而

式中 h1——主片的厚度;
L1——主片的长度;
fc——满载静挠度;
δ——挠度系数;
S——夹紧螺栓中心距;
k——无效系数,可取为0.5。
②弯矩量参数a在M1已定的情况下,决定着正弯矩或负弯矩的总量。它可根据总片数n的大小取值为

由式(3-98)计算的数值,是在给定n的条件下a可能的取值范围的均值。例如,n=8时,a可以在1~5的范围内取值;n=11时,a可以在1~8的范围内取值。
③等曲率角θ是为了简化生产工艺,保证在(a+2)~(n-2)区间内的各片具有同一曲率半径而给定的。此处a是弯矩量参数a的整数部分。θ值可按下式计算:

式(3-99)中的Ia+2和δa+2是第(a+2)片的惯性矩和厚度。α为非单一圆弧系数。此处,当各片等厚时可取为α=1.06,当各片不等厚时可取为α=1.20。
④Ma+2:平衡弯矩Ma+2是第(a+2)片的预应力的弯矩值。其定值原则是必须保证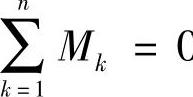 。它可计算为
。它可计算为

式中
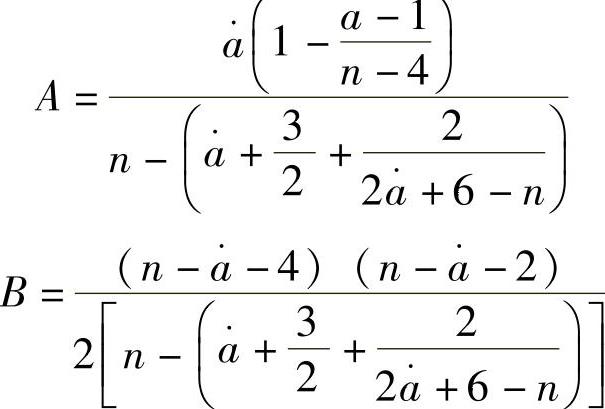
注意:计算时,式(3-100{的M1应以正值代入。
系数A、B还可直接从表3-17取值。
表3-17 系数A、B的数值

确定了上列参数,弯矩曲线图就确定了。有了弯矩曲线图,就可以方便地计算出各片的弯矩和预应力。如下所述。
第2片的弯矩为
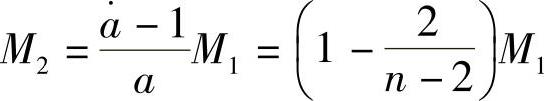
第n-2片的弯矩为
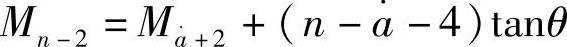
第n-1片的弯矩为

下面以3号簧的有关参数为例,来计算各片的弯矩和预应力。
3号簧所要求的总成曲率半径R0=150.8cm,静挠度fC=7.7cm,夹紧长度S=13cm,各片厚度hk=0.7cm,宽度b=6.5cm,各片长度见表3-18。
表3-18 3号簧各种长度

现分别计算未知参数:
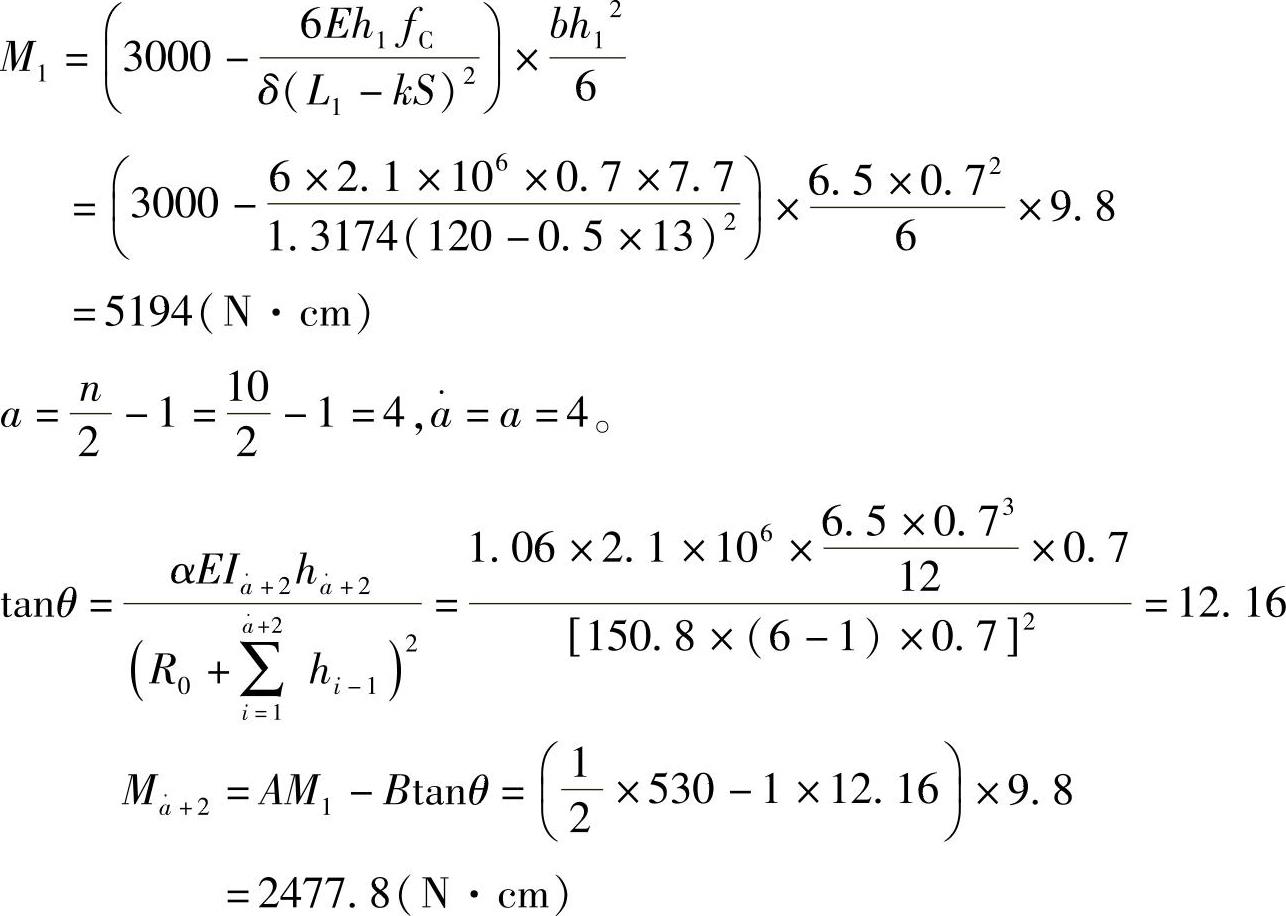
利用所得参数,便可作出如图3-40所示的弯矩曲线图。
由图3-40算出的各片的弯矩Mk和预应力σ0k见表3-19。

图3-40 弯矩曲线
表3-19 各片弯矩及预应力

2)各片曲率半径的确定。
在已知各片厚度hk、预应力δ0k以及总成曲率半径R0的情况下,可确定各片的曲率为
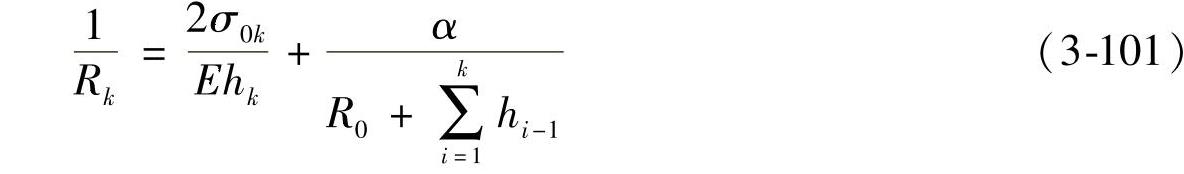
式(3-101)中的α是待求的非单一圆弧系数。下面就来推求在此情况下α的计算公式。
先将式(3-91)改写为
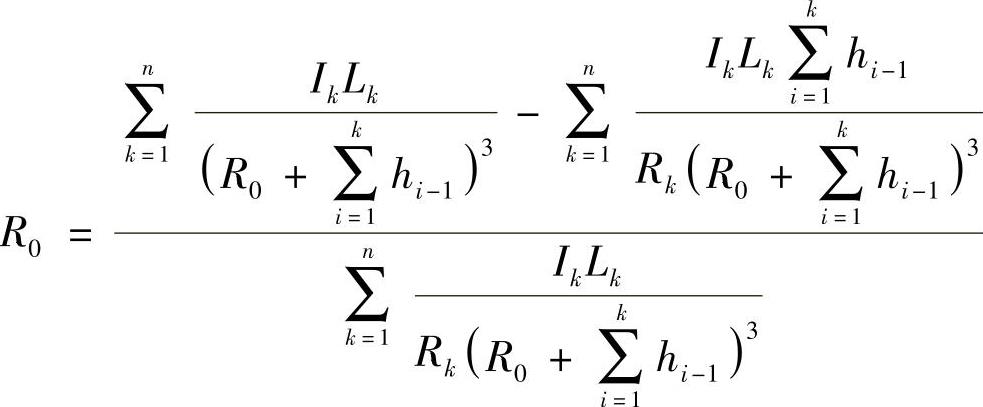
再将式(3-101)代入上式,便可得到
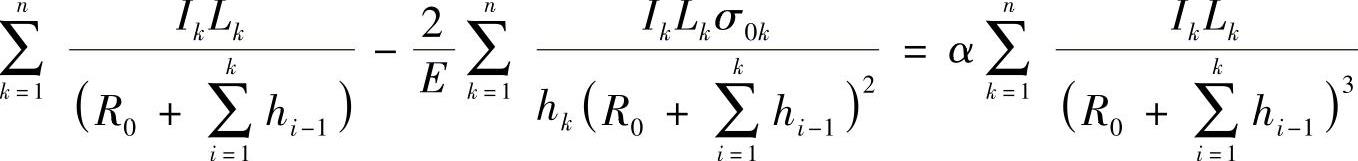
解之可得
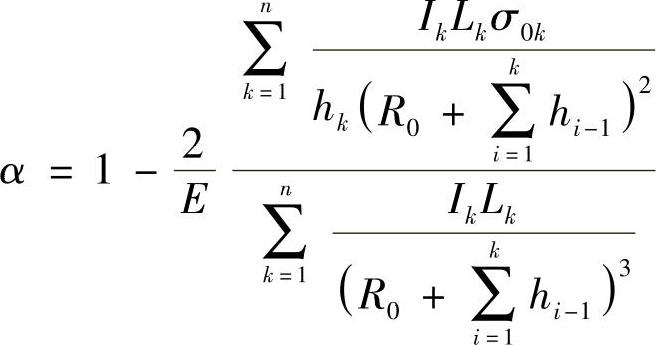
此公式表示为各片不等厚、考虑片厚影响的情况。
各片等厚、考虑片厚影响的情况下,有
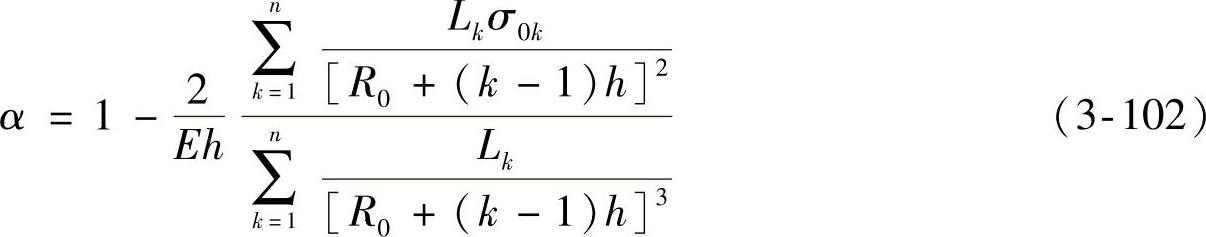
各片不等厚、不考虑片厚影响的情况下,有

各片等厚、不考虑片厚影响的情况下,有

下面先以3号簧为例,采用式(3-103)来计算α值,然后再利用所得α值代入式(3-101),分别计算各式的曲率半径Rk。α的计算表格及结果见表3-20。
表3-20 α的计算结果(R0=150.8cm)
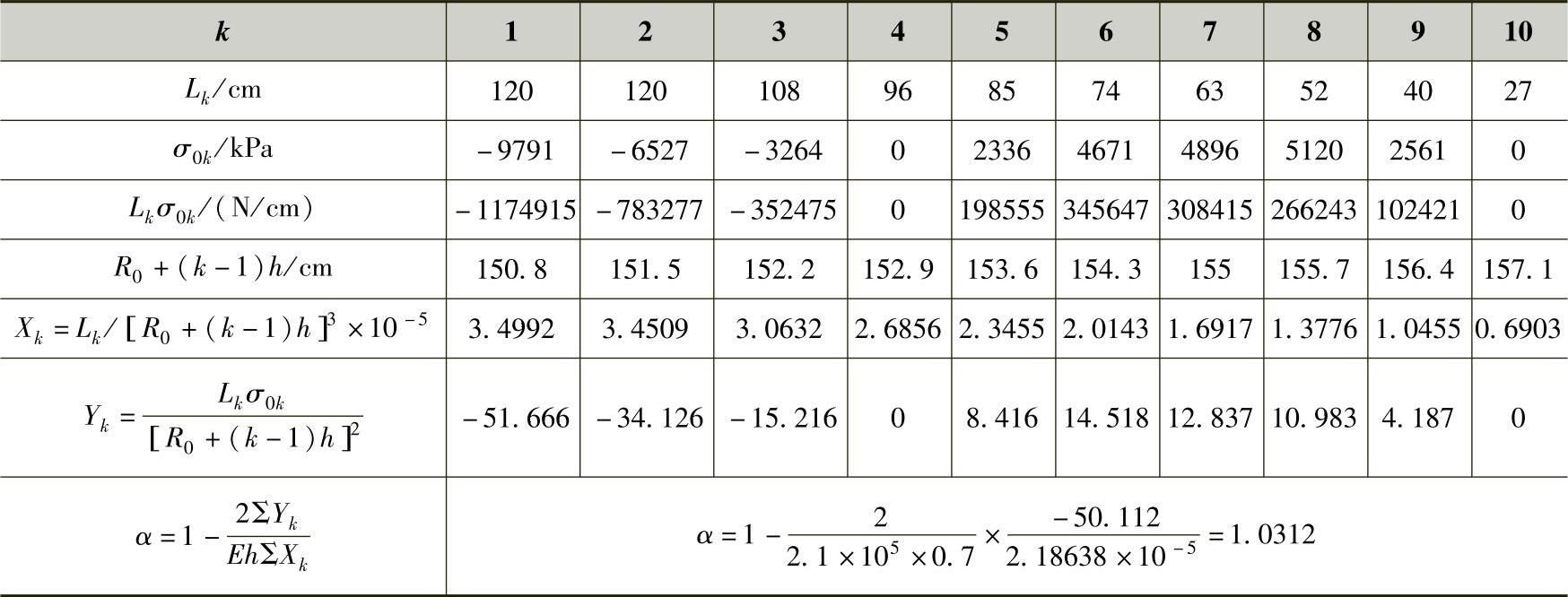
Rk的计算值和圆整值见表3-21。
表3-21 Rk及其圆整值

由表3-21中的数字可知,按此方法确定的Rk值和3号簧的Rk值是不一样的。这除了3号簧在设计时考虑要一簧两用,既装于某救护车的前悬架,也装于后悬架。前悬架静应力σ静前=39227kPa,而后悬架静应力σ静后=43149kPa,此处只按σ静=39227kPa考虑,因而除主片预应力偏小,R1也就偏小之外,更重要的还是计算方法不一样。
按此方法确定各片的弯矩、预应力和曲率半径是较为简明的。特别是弯矩量参数a按均值选取是较为稳妥的。对于总片数n较大的情况,简化工艺的优点也是明显的。例如,n=10的3号簧就有三片曲率半径相同。如果第4片和第9片我们也强行取为一致,则就只有7种不同的曲率半径了。
4.总成及单片应力
(1)总成应力
在《汽车设计》及有关资料中,总成根部静应力σA(MPa)通常计算为

然而,该式有几个值得研究的问题。
①该式中的片厚h只适合各片等厚的弹簧,至于变断面簧,h应以各片均值应力厚度的均值来代替。
②该式中的δ反映不出各片实际长短的变化,对变断面簧就更难确定。
③该式是将整副弹簧化为一个梯形单片来建立的,且只认为片端作用一个向下的力。实际弹簧的各片不仅在lk的片端处受有一个向下的力Pk,而且还在中部lk+1处受有一个向上的力Pk+1。因此,用该式计算的结果,总是大于各片根部应力的平均值。
鉴于上述情况,建议直接采用集中载荷法的各片根部应力的平均值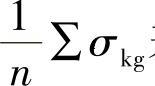 来替代总成应力,即令
来替代总成应力,即令
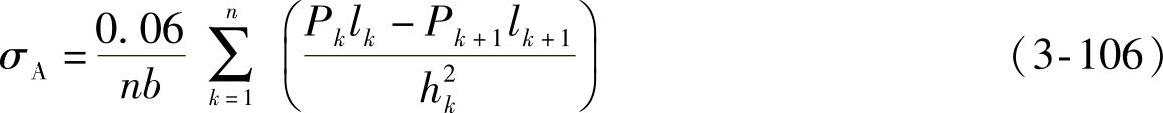
要求式(3-106{的计算结果不应超过材料许用应力的75%。
计算示例1
示例弹簧参数及计算过程见表3-22。
如果选材料为38SiMnVB([σA]=1800~2000MPa)、60Si2CrVA和50CrV4等材料,则总成根部静应力为1286MPa将是允许的。
表3-22 总成根部均值应力的计算(b=7cm)

(2)单片弯矩和应力
各单片任意断面的应力σkx(MPa)为

式中 Wk——各片断面系数,Wk=bh2/6(cm3);
Mkx——各片任意断面的弯矩(N·cm)。
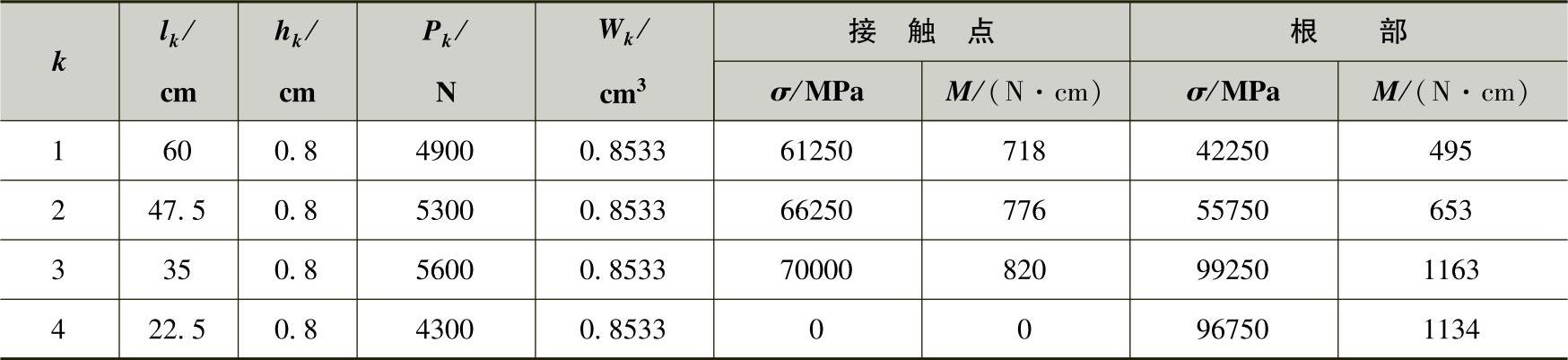
计算弯矩时,x应从各片片端计起。计算示例2
示例计算只计算接触点和根部的弯矩和应力。示例弹簧参数、片端力以及计算结果一并列入表3-23之中。由表可知,第3片和第4片根部弯矩和应力值较高,但选用优质钢材也是允许的。接触点和根部的弯矩如图3-41所示。
表3-23 单片弯矩及应力 (b=8cm)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








