研究对称板簧的运动特性，首先要摸清它的导向机构，摸清主叶片中心点的运动规律，即要找出它的运动瞬心，包括悬架中心以及轨迹半径及其与水平面的夹角等。

1.轨迹中心和轨迹半径所谓轨迹半径，指的是主叶片中心点的轨迹半径R，也叫“推杆”。C′点是M′点的轨迹中心，在已知板簧主片伸直长度L和夹紧距离d的情况下，轨迹半径的长度可近似表示为

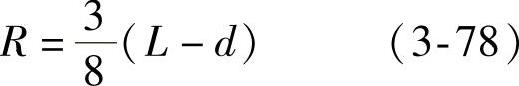
图3-30中的点C就是悬架中心，是相关点车轮着地中心M的轨迹中心，它是按平行四边形法则将C′点平移的结果。因此，也把CM（长度为R）叫做“推杆”。对于其他相关点的轨迹中心，均可按平行四边形法则求得。

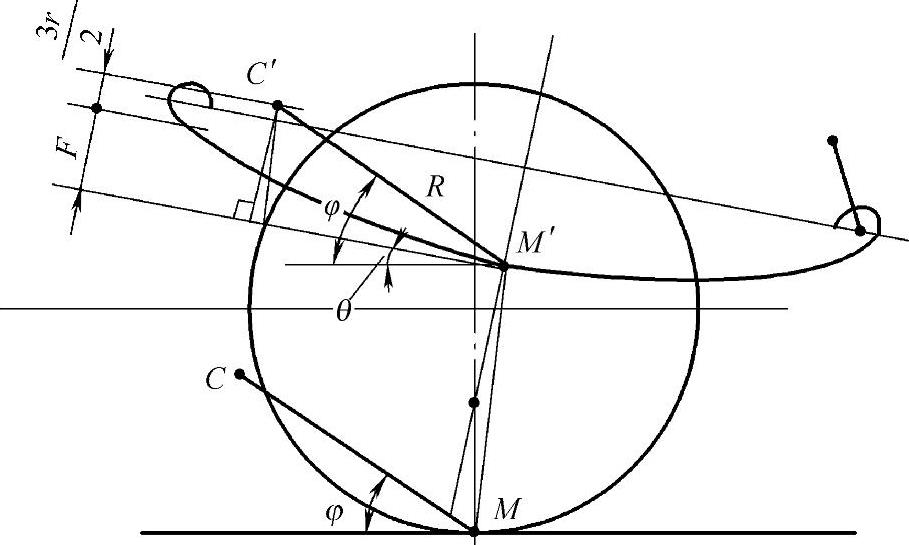
图3-30 对称板簧的“推杆”角

2.“推杆”角φ(www.daowen.com)

“推杆”角φ是指在满载状态下，“推杆”（轨迹半径）CM与地平面的夹角。在已知板簧相对于水平面的夹角为θ、满载弧高为F、板簧卷耳半径为r、C′为板簧主片中心M′的轨迹中心的前提下，由图3-30的几何关系可得对称板簧的“推杆”角为

式中，F后的正负号，上卷耳式取正，下卷耳式取负，对称式（柏林式）2r/3为0；θ前的正负号，板簧前（后）倾，摆耳在前（后）取正，板簧后（前）倾，摆耳在前（后）取负。

由式（3-79）可知，对前桥来说，板簧满载弧高为正、后倾布置、摆耳在后端的悬架，φ₁不仅在第二象限，且数值较大；对后桥来说，满载弧高为负、前倾布置、摆耳在后端的悬架，φ₂不仅在第三象限，且数值较大。这两种情况合在一起，是纵向力矩臂e_l增大的典型情况，对车身稳定性是最为不利的。然而，根据三正切定理，此种情况对转向特性却是最为有利的。

当φ₁在第二象限时，δ₁为正值（车桥回转方向与转弯方向相反）；当φ₂在第三象限时，δ₂为负值（车桥回转方向与转弯方向一致）。所以，前、后桥偏离角差Δ=δ₁-（-δ₂）增大，增强了不足转向趋势，如图3-29所示。

上述分析也说明了车身稳定性和操纵稳定性总是矛盾的。此种矛盾情况，任何悬架都不例外，不同之处，仅是影响ϕ的数值和方向的是悬架形式和杆系参数。式（3-79）既可用来评价车身稳定性，也可用来评价操纵稳定性。正如上节所述，ϕ值的大小还牵涉很多问题，因此不宜过分追求纵倾力矩臂的大小，而应全面考虑。