【摘要】:在悬架设计中,必须要知道弹性元件的受力或力矩,否则无法进行弹簧设计。N力的分力Ncos和弹簧力的分力Fscosθ分别对臂端Dd取矩有式中 φ2——下臂相对于水平面的夹角;θ——螺旋弹簧轴线与下臂垂直线的夹角。由此可得螺旋弹簧的轴线力为2.螺旋弹簧装在上臂上下臂为二力杆,P、Q、N三力汇于O点,故有故弹簧受力为图3-25 螺旋弹簧装于上臂的受力3.扭杆装在下臂上扭杆装在下臂上,故上臂为二力杆。
在悬架设计中,必须要知道弹性元件的受力或力矩,否则无法进行弹簧设计。如何求出弹性元件的受力(力矩)呢?这在双横臂悬架中可分为四种情况来研究:螺旋弹簧装在下臂上;螺旋弹簧装在上臂上;扭杆弹簧装在下臂上;扭杆弹簧装载上臂上。
1.螺旋弹簧装在下臂上
在螺旋弹簧装于下臂之上,在已知车轮满载静载荷P的情况下,可利用图3-24的关系来推求螺旋弹簧轴线方向的受力Fs。
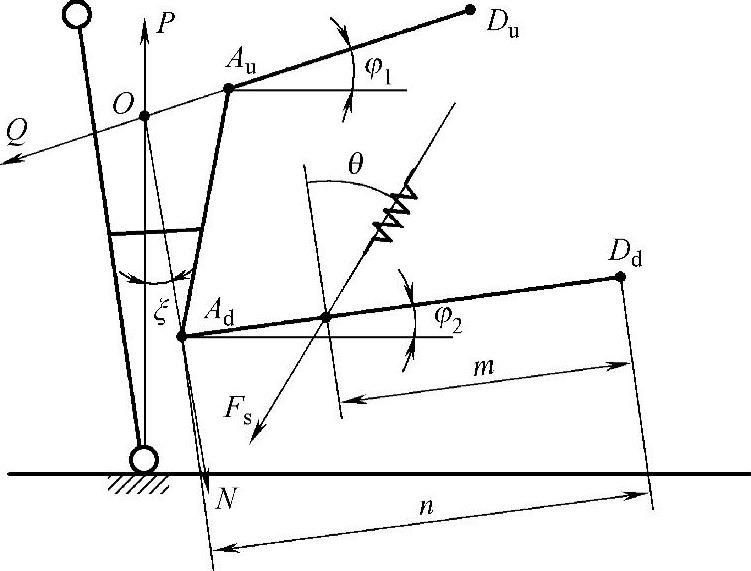
图3-24 螺旋弹簧装于下臂的受力
由于弹簧装在下臂之上,故上臂为二力杆,力P、Q和N汇交于O点,故有
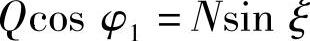

所以有
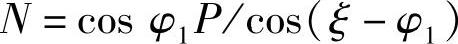
式中 φ1——上臂相对于水平面的夹角;
ξ——N力线与垂直平面的夹角。
N力的分力Ncos(ξ-φ2)和弹簧力的分力Fscosθ分别对臂端Dd取矩有
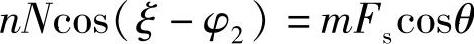
式中 φ2——下臂相对于水平面的夹角;
θ——螺旋弹簧轴线与下臂垂直线的夹角。
由此可得螺旋弹簧的轴线力为
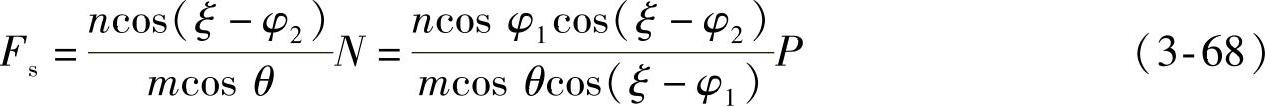
2.螺旋弹簧装在上臂上
下臂为二力杆,P、Q、N三力汇于O点(图3-25),故有
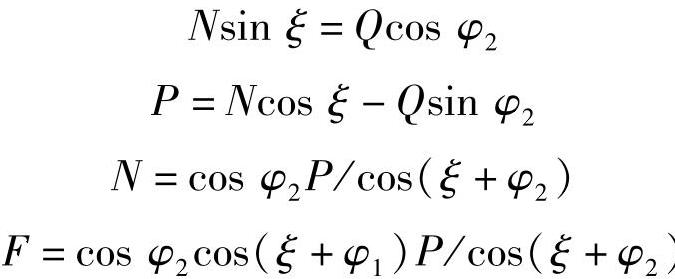
故弹簧受力为
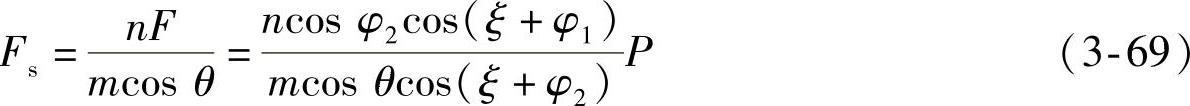
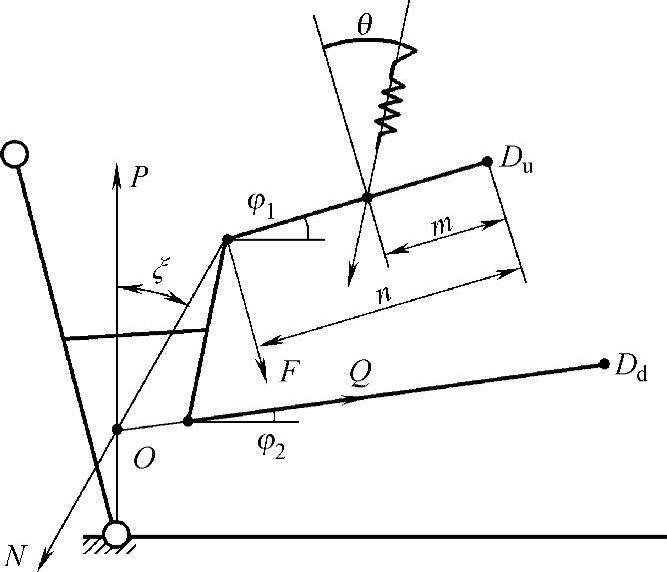
图3-25 螺旋弹簧装于上臂的受力
3.扭杆装在下臂上
扭杆装在下臂上,故上臂为二力杆。P、N、Q三力汇于O点,如图3-26所示,故有(https://www.daowen.com)
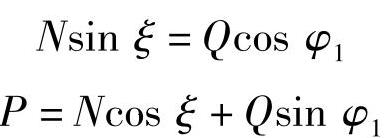
于是
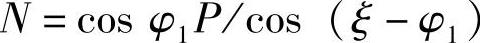
扭杆端部受力为
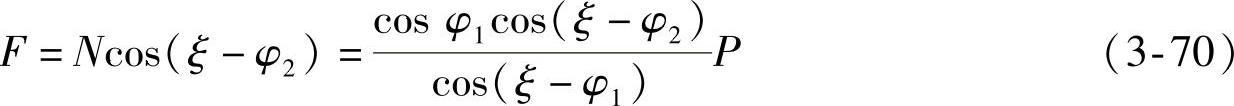
扭杆承受的扭矩为
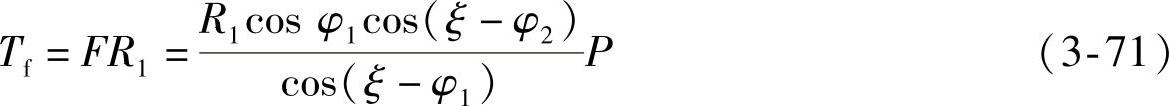
式中 φ1、φ2——上、下臂与水平面的夹角;
ξ——N力线与垂直平面的夹角。
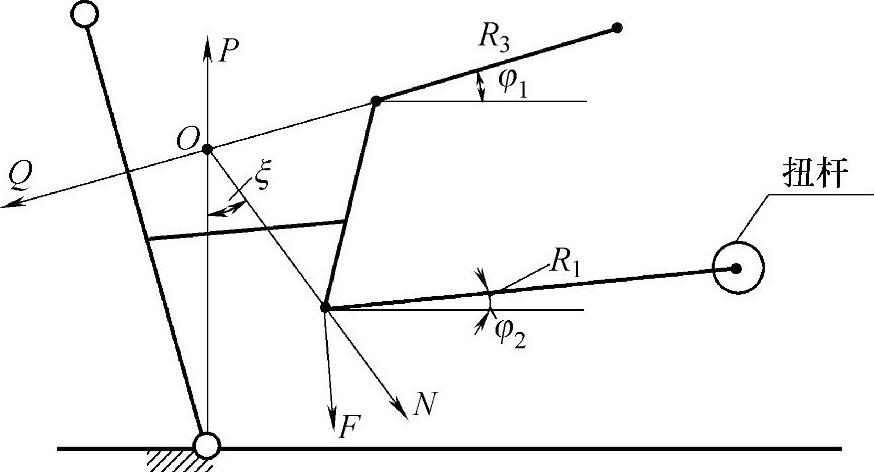
图3-26 扭杆装在下臂上的受力
4.扭杆装于上臂上
扭杆装在上臂上,故下臂为二力杆。P、Q、N三力汇于O点,故有
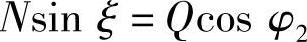
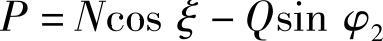
于是
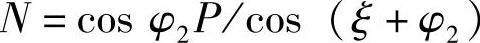
扭杆端部受力为
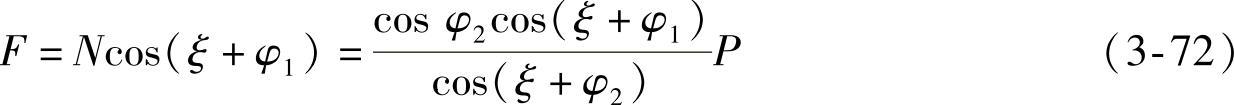
扭杆承受的扭矩为
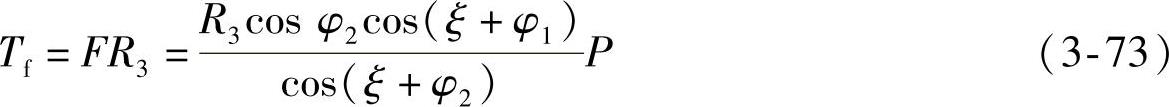
式中 φ1、φ2——上、下臂与水平面的夹角;
ξ——N力线与垂直平面的夹角。
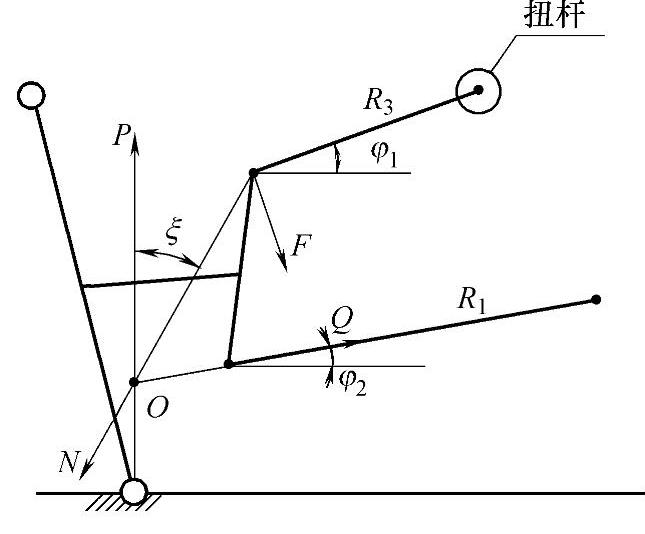
图3-27 扭杆装在上臂上的受力
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







