悬架运动学特性是指当车轮跳动时，前轮定位参数、轮距、前轮侧向滑移量等参数相应变化的规律。这一规律是由导向机构所决定的，它直接影响汽车的使用性能，特别是操纵稳定性、平顺性、转向轻便性和轮胎的使用寿命等。

1.车轮初始定位参数

（1）主销内倾角和后倾角

主销内倾角和后倾角均定义为正，反之为负。主销内倾角γ_i与后倾角γ_r可根据A_u、A_d两点的坐标由式（3-41）和式（3-42）计算为

（2）车轮外倾角和前束角

车轮外倾角γ_o由轮心O与接地点E的坐标确定，定义车轮外倾角外倾为正。外倾角用式（3-43）计算为

式中 R——轮胎的静半径。

车轮的前束角θ_T由车轮的轮心O与接地点E的坐标确定，定义前束角内收为正。前束角用式（3-44）计算为

（3）主销后拖距及内倾距

设主销延线与地面的交点为P，其x、y坐标分别为

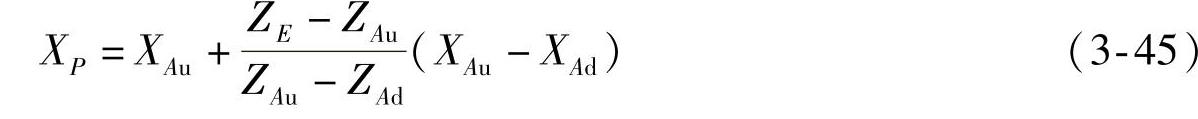
从而主销的后拖距a_r为

主销的偏移距a_i为

2.导向机构随下臂或上臂的运动关系

导向机构随摆臂运动的问题是三维空间的问题，此处把它放在YZ平面内的二维空间来处理。其理由是，在理论上我们认为A_u、D_u、A_d、D_d、E（O₃、O₄、O₂、O₁、O₅）五点的x轴坐标相等，这就是说，这个问题本来就是个平面问题，何必把问题复杂化呢？再则是在二维空间内，可以轻易地获得显式函数的结果，使问题大为简化。

此处利用简明的复数法来建立机构随下臂或上臂运动的数学模型。在所研究的问题里，导向机构其实就是一个“四杆机构”，如图3-19和图3-21所示。我们把“四杆机构”的杆长设为R_k（k=1，2，3，4），若弹性元件装于下臂之上，则杆R₁这个下臂就是主动臂。作用于主动臂臂端A_d（O₂）点的力（力矩）使下臂绕枢轴点D_d（O₁）反时针旋转。

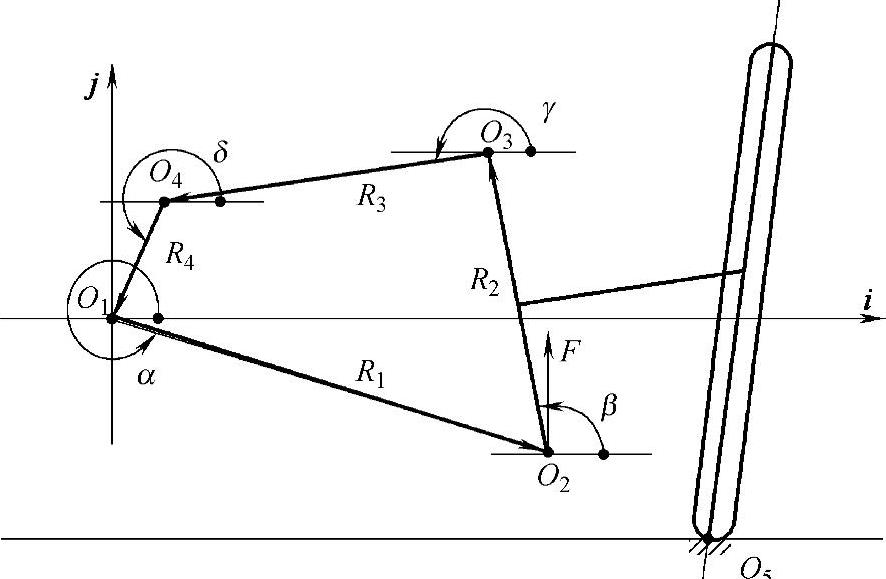
图3-21 导向机构的运动规律

假设下臂转过了α角，其他各杆转角分别为β、γ和δ。由于R_k和δ为已知参数，α为独立变量，要推求的只有β和γ。

若弹性元件装于上臂之上，则杆R₃这个上臂就是主动臂。作用于主动臂臂端A_u（O₃）点的力（力矩{使上臂绕枢轴点D_u（O₄）逆时针旋转。假设上臂转过了γ角，其他各杆的转角分别为α、β和δ。由于R_k和δ为已知参数，γ为独立变量，则要推求的只有α和β。

在图3-21中，“四杆机构”全部为铰点，且复数R_k构成封闭环路，即

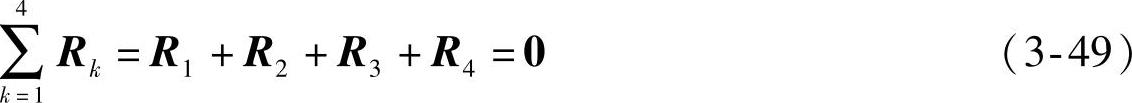
按指数写法为

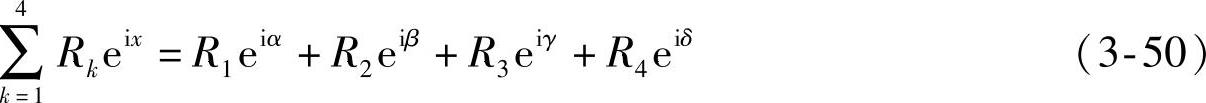
根据欧拉公式有

所以，复数实部为

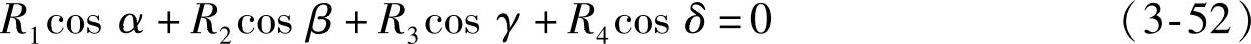
由复数虚部得

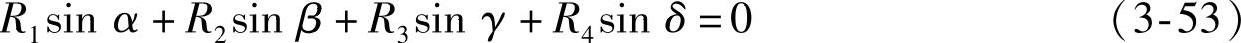
若弹性元件装在下臂上，则α为独立变量，故可由式（3-52）和式（3-53）解得

(www.daowen.com)

式中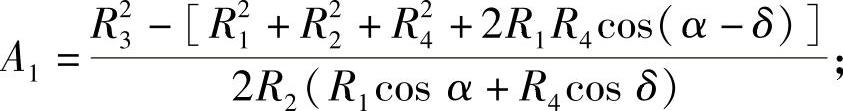

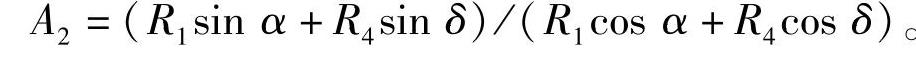
在已知β后，由式（3-53）可解得

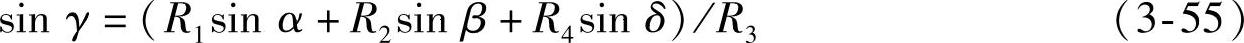
若弹性元件装在上臂之上，则γ为独立变量，故可由式（3-52）和式（3-53）解得

式中；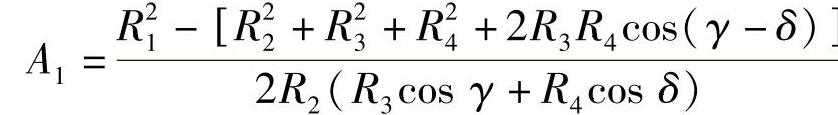

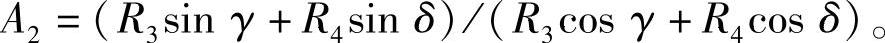
在已知β后，由式（3-53）解得

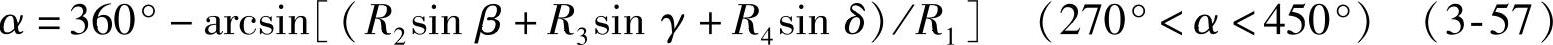
3.车轮着地点随摆臂运动的关系

在图3-22中，弹性元件无论装在下臂上还是装在上臂上，车轮着地点的变化都是由R₁、R₅、R₆、r_K和R所构成的闭环决定的。因此，复数R以及对应的x、y便可由式（3-58）～式（3-60）给出

4.相关参数与摆臂运动的关系

相关参数指轮距B、车轮外倾角ξ_o、主销内倾角ξ_i、悬架中心C和力矩中心O等，如图3-23所示。

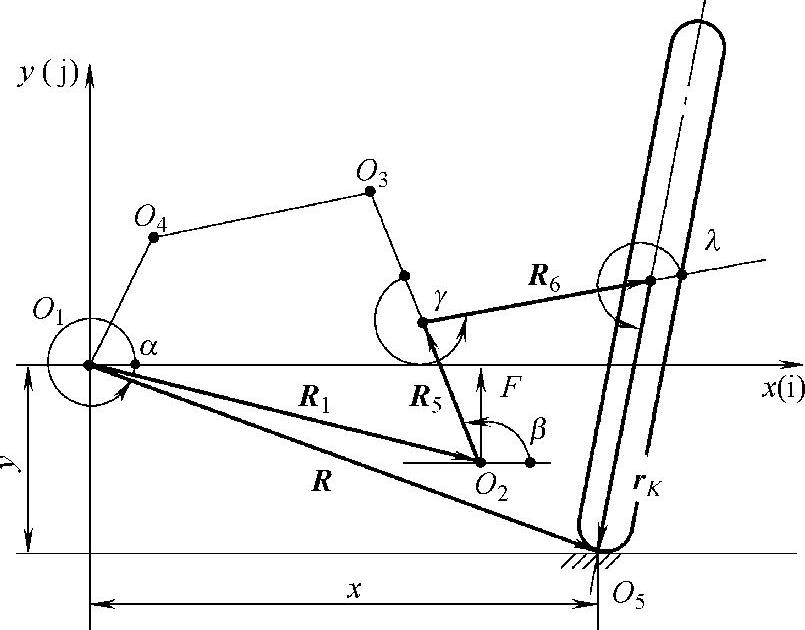
图3-22 车轮着地点随下臂运动的关系

图3-23 相关参数与摆臂运动的关系

这些参数不但随摆臂的运动而改变，而且对悬架刚度、行驶稳定性和车身稳定性等都有至关重要的作用。

根据图3-21～图3-23的关系，加之已经导出的结果，便可得到下列相关参数的表达式。

（1）车轮外倾角ξ_o

（2）主销内倾角ξ_i

式中 ξ——主销与杆O₂O₃（R₂)的夹角。

（3)轮距

式中 S——左、右悬架摆臂枢轴点间的距离。

（4）杠杆参数l₁、l₂

杠杆参数l₁和l₂不仅是确定悬架中心C和力矩中心O的过渡参数，也是推求悬架刚度必不可少的参数。由图3-23的几何关系可得

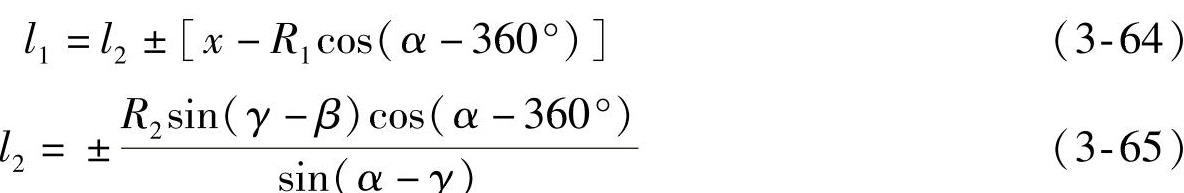
（5）悬架中心C的纵坐标h

对于式（3-64）～式（3-66）中的“±”号，摆臂内交者取正，反之取负。

（6）力矩中心O的纵坐标H