在绘出双横臂悬架空间模型的前提下，列出相关点的坐标，并利用这些坐标确定上下摆臂的坐标，然后利用YZ平面和XZ平面的模型确定悬架中心和力矩中心。

1.空间模型

双横臂悬架空间模型如图3-17所示。图中除上、下三角架外，还有扭杆、减振器以及转向机构等。相关点的坐标列于表3-1中。

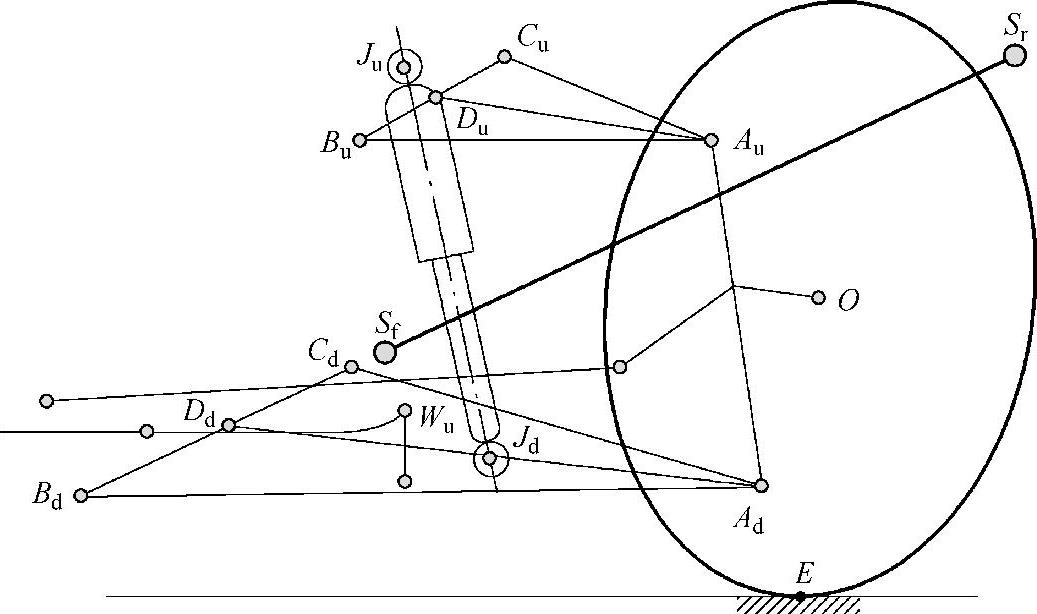
图3-17 双横臂悬架空间模型

表3-1 双横臂悬架相关点的代号及坐标

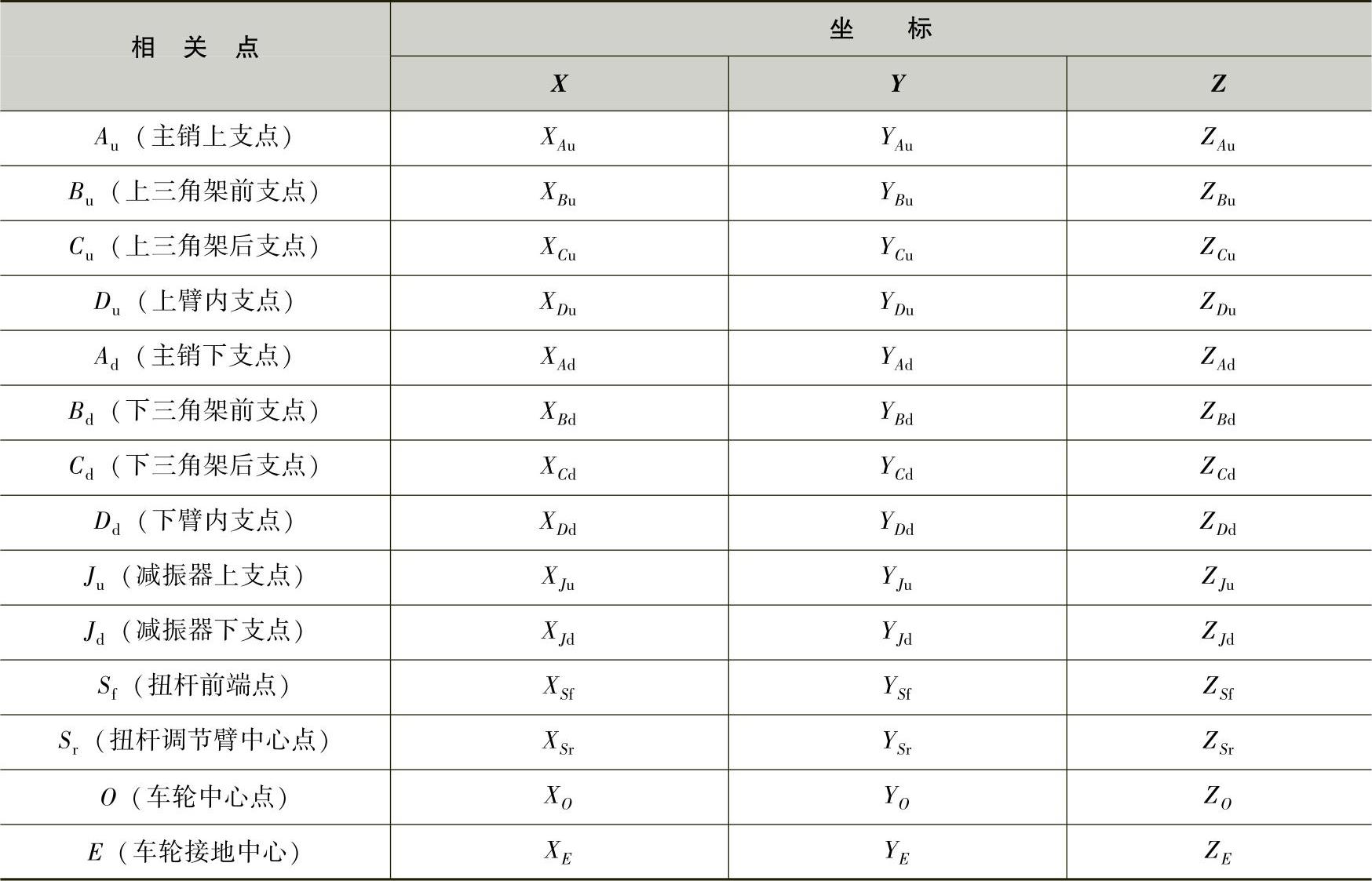
2.上下臂的坐标

双横臂悬架常做成双叉杆式或A臂式，如图3-17所示。它利用上三角架A_uB_uC_u和下三角架A_dB_dC_d将车轮和车身联结起来。为简化分析和计算的需要，常将上、下三角架各简化为摆臂，也就是图3-17中的A_uD_u和A_dD_d。因此确定上、下臂的坐标，也就是在已知三角架三点A、B、C的坐标的情况下，确定D_u和D_d两点的坐标。确定的具体步骤如下所述。

（1）计算“三角架”各边的空间长度

设x、y、z为“三角架”各点的坐标，那么“三角架”各边的实际长度可根据图3-18的关系利用下列三式计算：

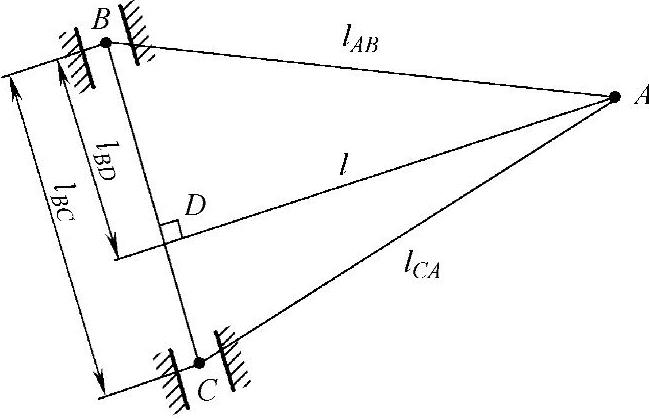
图3-18 摆臂坐标的确定

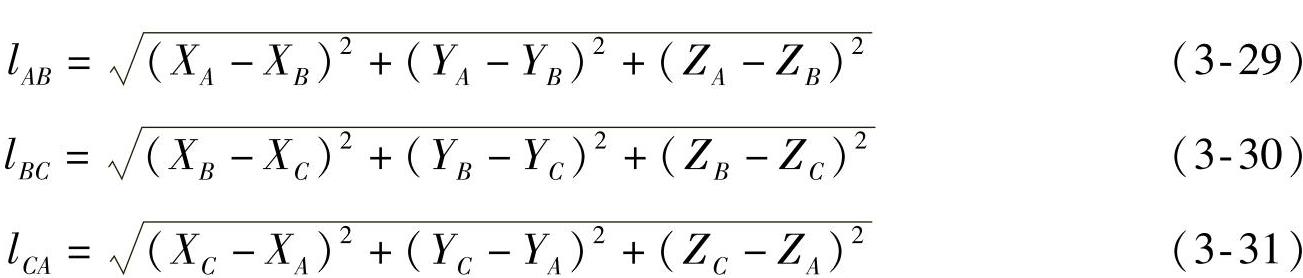
（2）确定臂端坐标

在实际边长的三角形中，过点A所作边长l_BC的垂线AD（长度为l）便是臂长，其垂足D便是臂的另一端点，与点D相关的BD（长度为l_BD）和臂长AD（长度为l）可用下列两式计算：

式（3-32）中，垂足在三角形中部或在外下部者取正，其余取负。

垂足的坐标可用下列公式计算：

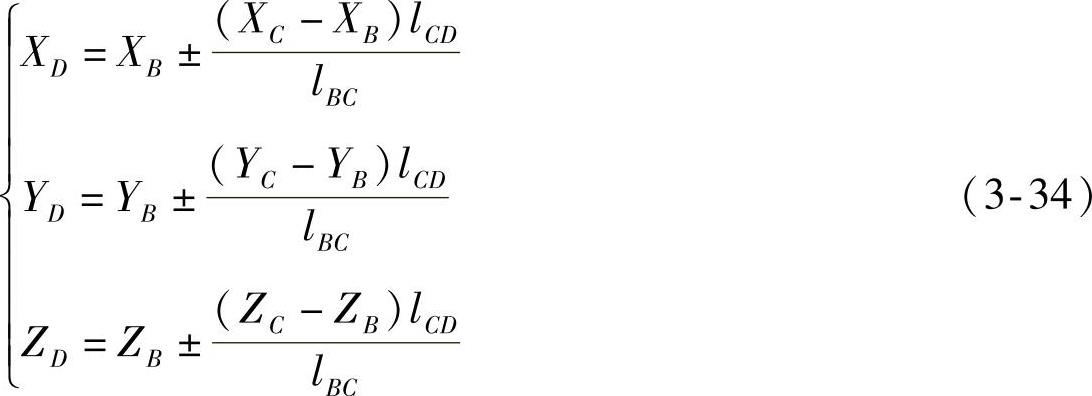
垂足在△ABC中部者取正号，其余为负号。

3.悬架中心和力矩中心

为方便求出横向悬架中心和纵向悬架中心，把模型分别建立在YZ平面和XZ平面上。(www.daowen.com)

（1）横向悬架中心和侧倾力矩中心

横向导向机构分别由上臂A_uD_u和下臂A_dD_d构成，如图3-19所示。它属于摆臂外交式。

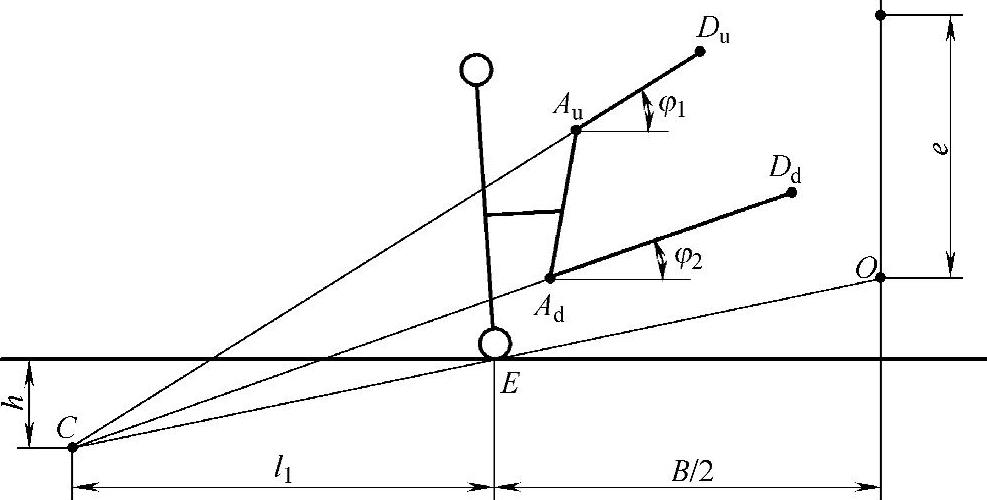
图3-19 横向导向机构

点A_u、D_u以及A_d、D_d的连线的延长线汇交于车轮外侧的点C，此点便是横向悬架中心。请注意A_uD_u和A_dD_d是满载时的空间直线，其延长线不一定交于一点。正因为如此，在设计时，务必要保证A_u、D_u、A_d、D_d、E五点基本共面，即应使其x轴坐标基本相等。因此，上、下“三角架”的设计是不可随便的。

点C与车轮着地中心点E的连线的延长线与车身中心线（中性面）的交点O就是侧倾力矩中心。侧倾力矩中心与悬挂质体质心的高度差便是侧倾力矩臂e。

横向悬架中心C的位置由高度h和长度l₁决定，而在横向平面内上、下臂所在直线的方程为

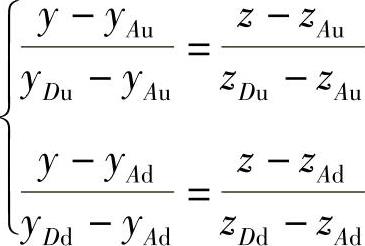
解此二方程，便可求出点C的坐标Y_C、Z_C，因此有

（2）摆臂角φ₁、φ₂

摆臂角可根据A_u、D_u、A_d、D_d四点的坐标由下列两式计算

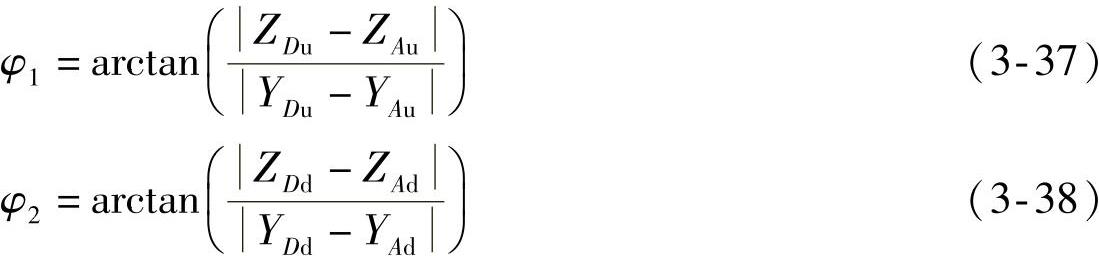
（3）纵向悬架中心

纵向导向机构是由上臂销轴B_uC_u和下臂销轴B_dC_d构成，两销轴延线的交点C_e就是纵向悬架中心，如图3-20所示。至于纵向力矩中心，则需要前、后悬架配合导出，参见第二章。

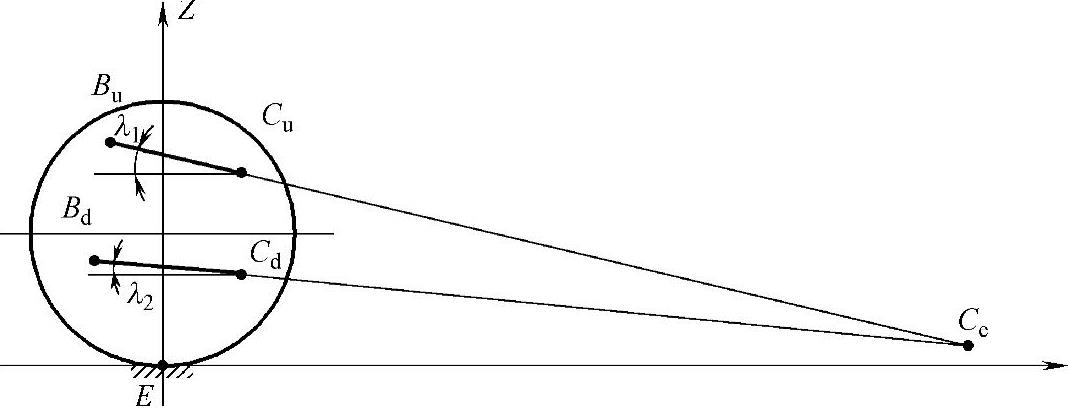
图3-20 纵向导向机构

（4）臂轴销角λ₁、λ₂

上臂轴销角λ₁与下臂轴销角λ₂可根据B_u、C_u、B_d、C_d四点的坐标，由式（3-39）和式（3-40）计算：