相关参数包括悬架中心、侧倾中心、枢轴偏角、摆臂仰角以及弹簧受力等问题，如图3-14所示。

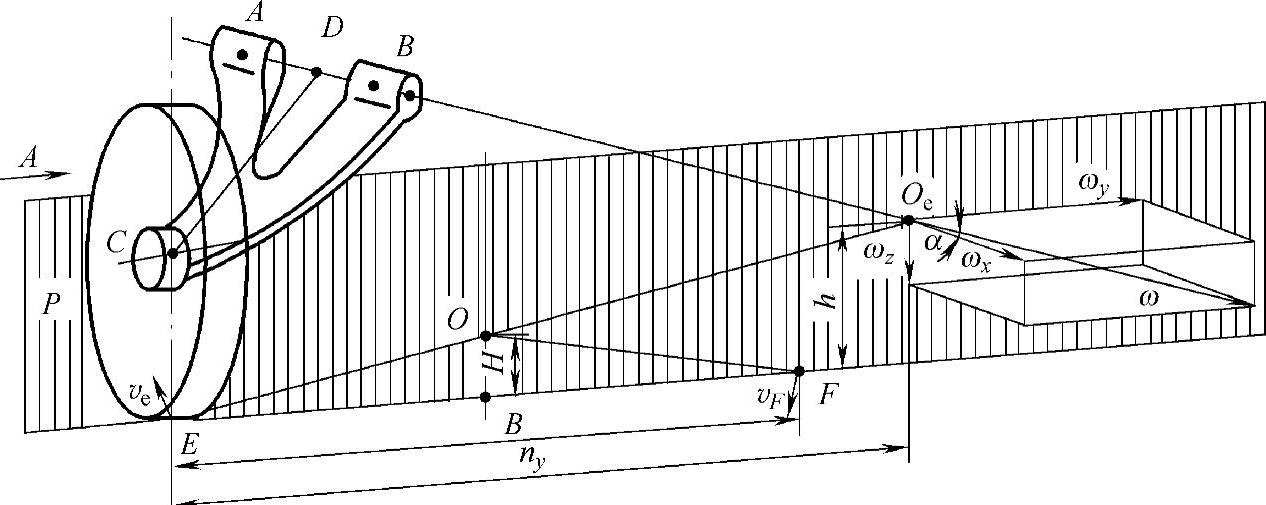
图3-14 半拖臂悬架的悬架中心、侧倾中心和枢轴偏角

1.悬架中心

所谓悬架中心，就是悬架（包括车轮总成）在满载状态下，相对于车身在横向平面（yz）内和纵向平面（xz）内的运动瞬心，也包括摆臂端点D。

（1）横向平面内的悬架中心

如图3-14所示，假设P平面、地平面和车身中心面的交点为坐标原点，其中P平面是过左右车轮着地中心E、F二点且垂直于地平面的平面。图中点O_e就是悬架的悬架中心。它是摆臂枢轴线（悬架轴线）在满载状态下，与P平面的交点。确定了点O_e的位置，就等于确定了侧倾中心点O。

之所以认定点O_e是悬架的悬架中心，是因为点O_e是摆臂枢轴线与P平面的交点，而摆臂枢轴线与摆臂相对于车身运动的角速度矢量ω的方向一致，如果在点O_e将ω按x、y、z三个坐标轴分解为ω_x、ω_y、ω_z三个分量，那么只有ω_x垂直于P平面。也就是说，O_e点相对于车身的由ω_x引起的速度分量v_e处于P平面内，故点O_e就是悬架（包括车轮总成）相对于车身运动的悬架中心。

为确定悬架中心点O_e的位置，只需确定点O_e的离地高度h和至车轮中心线的水平距离n_y即可。令枢轴线上A、B两点的坐标分别为X_A、Y_A、Z_A和X_B、Y_B、Z_B，那么由图3-14的A向视图（xz平面）的几何关系可得

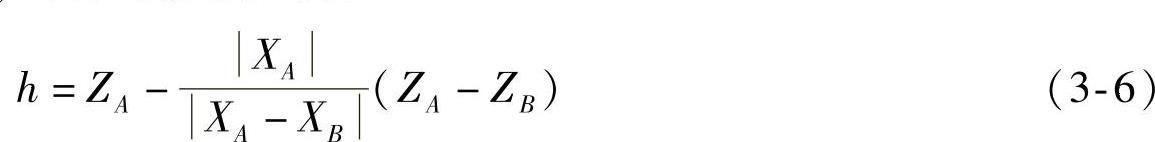
若h为负值，则说明点O_e钻入地下。

由图3-14所示（yz平面）的几何关系可得

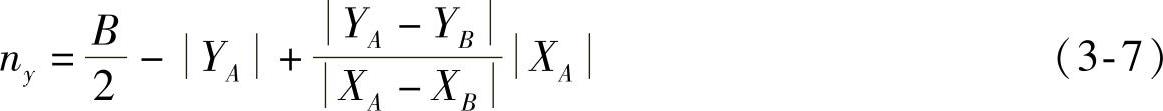
式中 B——轮距。

（2）纵向平面内的悬架中心

由确定横向平面内的悬架中心O_e的过程，可以想象纵向平面（xz）的悬架中心O_e′，应该是在满载状态下摆臂枢轴线与Q平面的交点。Q平面是过点E沿x轴轴线方向且垂直于地平面的平面。确定了点O_e′，可为求取力矩中心等参数创造条件。

要确定点O_e′的位置，只需确定该点的x坐标n_x和z坐标n_z即可。由图3-14的顶视图（xy平面）的关系可得

由图3-14侧视图（xz平面）的几何关系可得

2.侧倾中心

侧倾中心O就是在满载状态下，左、右悬架或者地平面相对于车身的运动瞬心。在车身质心面与横向中性面重合的情况下，侧倾中心就是在P平面内，车轮着地中心E和悬架中心O_e的连线与车身中心线的交点。因此，O点的高度H为

3.枢轴偏角

摆臂枢轴线的空间角度是半拖臂悬架的重要参数。它不仅影响悬架的刚度，而且还决定着整车的车身稳定性和操纵稳定性。枢轴线的空间角度是由枢轴线与X、Y、Z三个坐标轴线的夹角α、β和γ构成的。α、β和γ分别称为X、Y、Z三个方向的枢轴偏角。为计算刚度的需要，此处仅列出α（图3-14中角速度矢量ω与其分量ω_x之间的夹角）和β（ω与ω_y之间的夹角）的计算式为

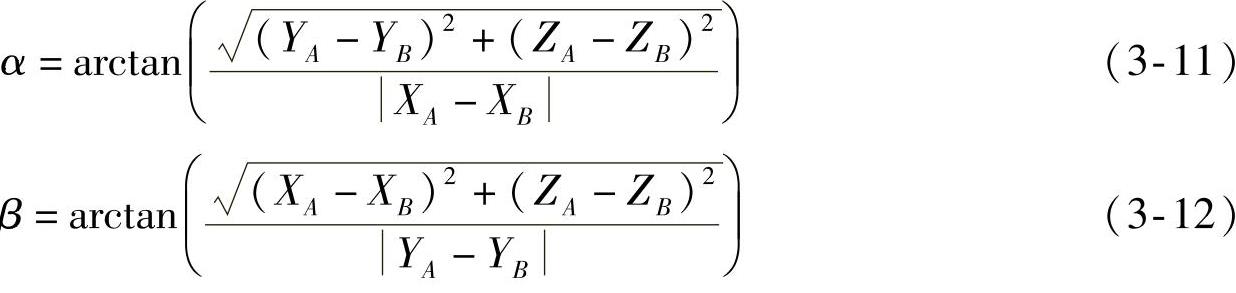(www.daowen.com)

4.摆臂仰角

摆臂仰角系摆臂CD相对于地平面的夹角，也就是图3-15中的θ。要确定θ，必先确定摆臂端点D的Z坐标Z_D，点D是过轮心C引枢轴线AB的垂线的垂足，如图3-15所示。

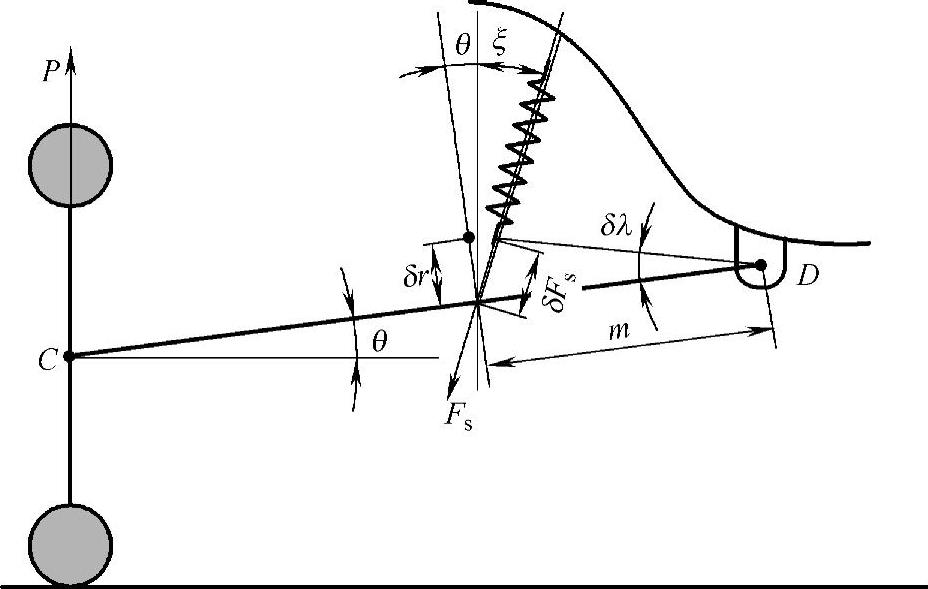
图3-15 半拖臂悬架的拖臂仰角

由于已知A、B、C三点的三维坐标，利用空间三角形△ABC的几何关系，可以求得△ABC垂足D（摆臂端点）的Z坐标为

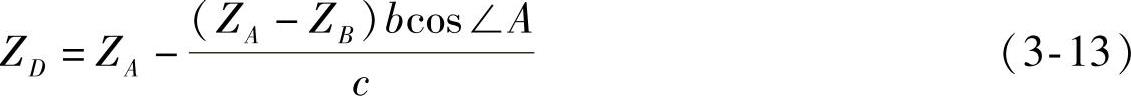
式中 ∠A——空间△ABC的顶角。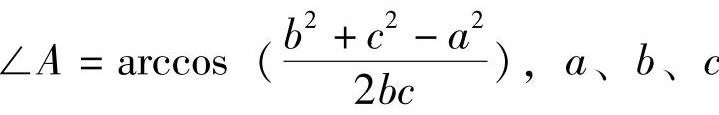为空间△ABC

的边长，其中

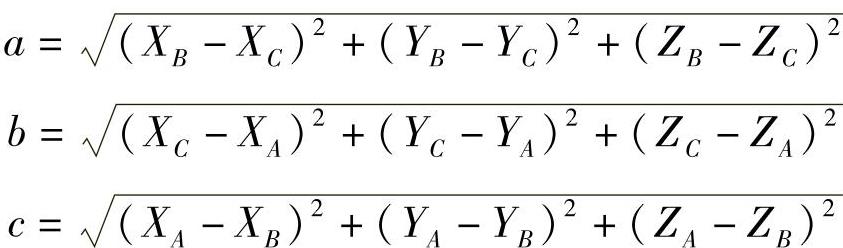
摆臂空间长度为

因此，由图3-15可得摆臂仰角为

摆臂的空间长度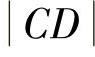在XY平面的投影长度，也就是杠杆n的长度为

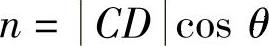
5.弹簧受力

在已知车轮载荷P的情况下，可先求垂直于摆臂CD的力F，然后再求弹簧力F_s。根据图3-15的关系有

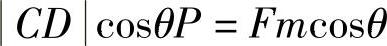
所以

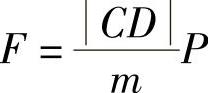
由此可得弹簧受力为

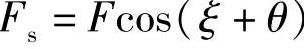
即

式中 ξ——螺旋弹簧轴线与垂直平面的夹角。