角刚度比是一个说明各车轴间角刚度匹配关系的参数。二轴汽车的角刚度比，就是前、后车轴角刚度的比值，即

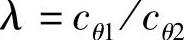
然而，在多轴汽车中，角刚度比的表达式却不那么简单。各轴角刚度的匹配关系不仅与汽车的转向特性有关，而且与汽车车身的受力情况有关，加之多轴汽车轴间关系的复杂性，对于角刚度比只能用不同的定义去研究不同的问题。

1.角刚度比与转向特性的关系

汽车在侧向加速度的作用下，将引起同一车轴内外车轮的负荷转移。负荷转移量的大小，也与该车轴的角刚度值成正比的。又由于弹性车轮的偏离系数与负荷的关系是一条上凸曲线，所以车轴偏离角的大小，也是与该车轴的角刚度值成正比的，如图2-20所示。

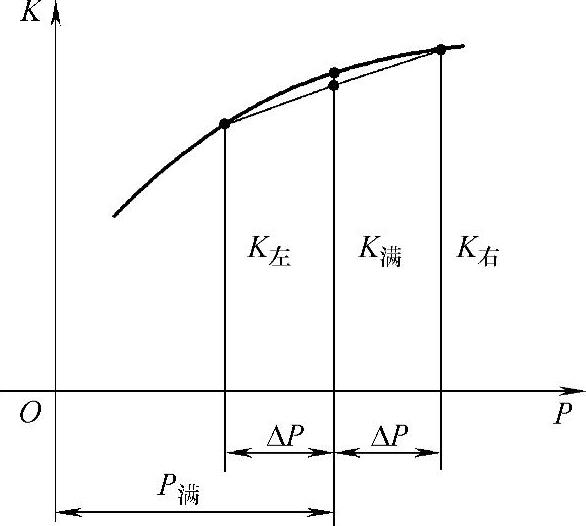
图2-20 载荷P和偏离系数K的关系

如果满载，轮胎的负荷为P_满，相应的偏离系数为K_满。而在侧向力P_y的作用下，左、右车轮负荷将发生变化。设左车轮为P_左=P_满-ΔP，则右车轮为P_右=P_满+ΔP。由于左、右车轮负荷的变化，偏离系数也随之变化。K_左＜K_满，K_右＞K_满，特别是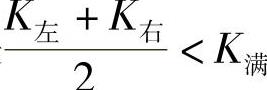。这就是说，平均K值下降了。

车轮的偏离角为

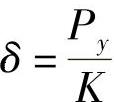
如果K值下降，则δ增大，也就是车桥偏离角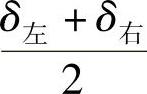加大了。

在二轴汽车中，如所讨论车桥是前桥，那就是δ₁增加了。而δ₁＞δ₂，便是不足转向趋势。

当前、后桥角刚度比λ=c_θ1/c_θ2＞1时，在侧倾力矩的作用下，分配于前桥的力矩就大，因而左右车轮负荷转移就较后桥大，平均K值就比后桥下降得多，偏离角前桥就大于后桥，从而增大了“不足转向”程度。

可见，在二轴汽车中：λ＞1是不足转向趋势；

λ=1是中性转向趋势；

λ＜1是过度转向趋势。

在多轴汽车的不同车轴上，由于角刚度不同，在同一侧向加速度的作用下，偏离角也就不一样。其中，任意两个不同偏离角的车轴，均可构成一个瞬心，构成一个新的转向趋势。也就是说，任意两轴间的角刚度比，均会对整车的转向特性造成影响：或者加强、或者削弱整车原始转向程度。所有的两两关系，其效果是有的加，有的减，有的严重，有的轻微。这是一个复杂的矛盾统一体，绝非一个简单的角刚度比所能描绘清楚的！

为了近似度量这一复杂事物，可在忽略轴间距影响的前提下，采用总角刚度比的概念来评价多轴汽车角刚度匹配所造成的转向特性趋势。

所谓总角刚度比，就是各低序号车轴的角刚度分别与各高序号车轴的角刚度，两两相比所得比值的和的均值。

假设车轴总数为n，那么各低序号车轴角刚度与各高序号车轴角刚度的比值一共有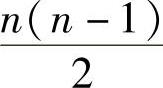项。所以总角刚度比为

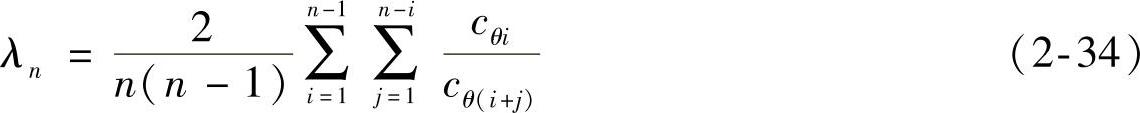
式中 n——总轴数；

i、j——轴序号；

λ_n——转向特性总角刚度比；

c_θi、c_θ（i+j）——各轴角刚度（N·mm/rad）。

总角刚度比是多轴汽车整车由于轴间角刚度的分配关系所造成的转向特性趋势的综合描述，有下述三种趋势：λ_n＞1，为不足转向趋势；λ_n=1，为中性转向趋势；λ_n＜1，为过度转向趋势。

2.角刚度比与车身受力的关系（等角侧倾问题）

汽车角刚度的匹配与车身受力有着紧密的关系。从理论上说，可以选择这样一个匹配，使车身承受遭致损坏的附加力矩；也可选择另外一个匹配，让车身完全不承受附加力矩。

汽车在侧向加速度j的作用下，侧倾外力矩M在各轴上的分配是不一定相等的，即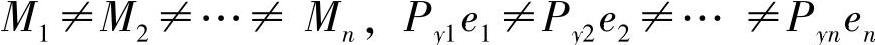。这不仅是因为悬挂质量在各轴上的分配不一定相等，侧向力P_yi不等，而且由于各轴悬架机构的不同，悬挂质体质心高度不等，侧倾力矩臂e_i也就不一定相等。

同时，汽车在侧向加速度的作用下，各轴的角刚度将提供一个反抗力矩。这个反抗力矩与外力矩构成平衡，即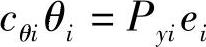。这就是说，车身在各轴处的倾角θ_i=P_yie_i/c_θi，由于各轴角刚度等因素的匹配不见得相应，θ_i值就不一定相等，于是车身将承受一系列的附加力矩。

如果各轴角刚度的匹配能与各轴的悬挂负荷P_i以及力矩臂e_i的大小相应，那么车身将保持等角侧倾而不承受这些额外的力矩。假设整车悬挂负荷为P，横向角刚度为c_θ，侧倾角为θ，则有

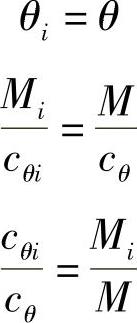
根据外力矩等于侧向力与侧倾力矩臂之积的关系，可得

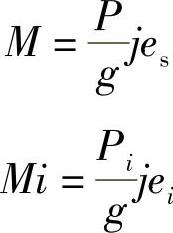
于是各相关车轴与整车的横向角刚度比为

当把式（2-12）的关系代入式（2-35）后，便可得到各相关车轴的等角侧倾角刚度比的表达式为

式中 λ_i——等角侧倾角刚度比；

l_i——相关车轴至质心面的距离（mm）；

c_i——相关车轴的线刚度（N/mm）；(www.daowen.com)

e_i——相关悬架的侧倾力矩臂（mm）；

R₀——外心距（mm）；

c——组合线刚度（N/mm）；

e_s——整车侧倾力矩臂（mm）。

由式（2-36）可知，等角侧倾角刚度比（相对角刚度）是和相对位置（l-l_i）/R₀、相对线刚度c_i/c和相对侧倾力矩臂e_i/e_s有关的。

注意，各轴等角侧倾角刚度比之和等于1，即

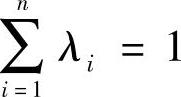
在分配各轴角刚度时，应尽量按公式c_θi=λ_ic_θ取值。特别是相邻车轴的角刚度值不可相差太多。

等角侧倾角刚度比的取值范围是个较为复杂的问题，下面以二轴汽车为例进行一简单分析，如图2-21所示。

二轴汽车等角侧倾角刚度比为

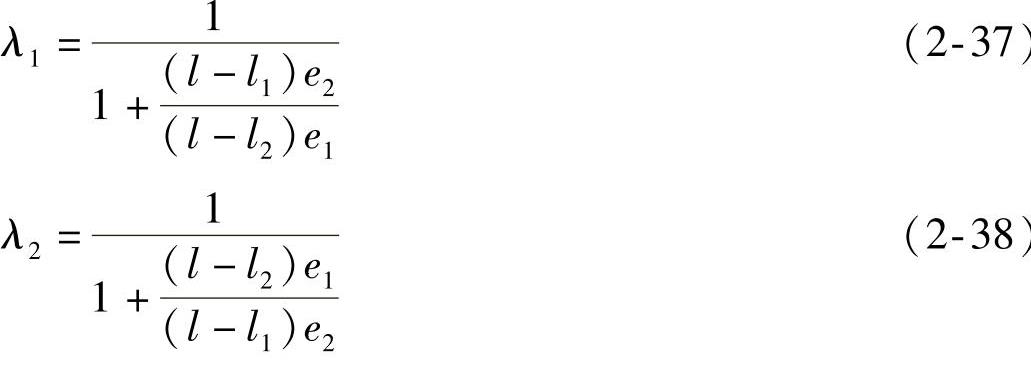
由式（2-37）可知，λ₁的数值完全取决于质心面的位置和力矩臂的大小。

作为质心面：当（l-l₂）=0时，质心落在后轴上，λ₁=0；当（l-l₂）等于轴距的半，即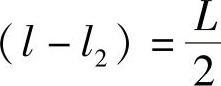时，若e_i=e₂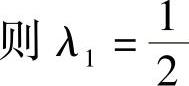，；当（l-l₂）等于轴距，即（l-l₂）=L时，质心落在前轴上，此时λ₁=1。

作为侧倾力矩臂：当e₁=0时，侧倾轴线通过前悬挂质体质心，λ₁=0；当e₁=e₂且l₁=l₂时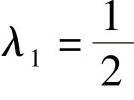，；当e₂=0时，侧倾轴线通过后悬挂质体质心，λ₁=1。

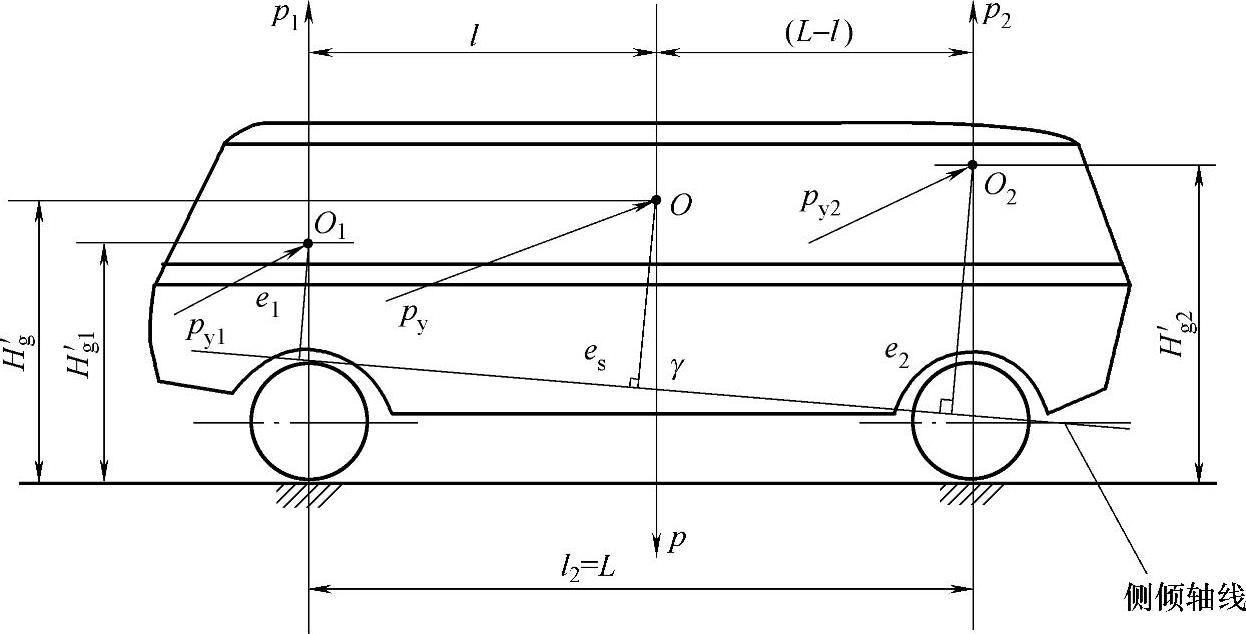
图2-21 二轴汽车侧倾受力

特别值得指出的是，前后轴悬架的侧倾力矩中心完全可能设计在侧倾轴线的异侧。这就是说，e₁或者e₂还可取得负值。当出现这种情况时，λ₁值便可远大于1了。例如，当e₁=-e₂时，若l₁=l₂，则λ₁→∞。这种情况下的车身，好似一条扁担遭受扭转。

从上述二轴汽车的分析可知，λ_i值一般以为中心左右波动，波动范围为0～1。当力矩臂e_i取得负值时，λ_i值则可大大超出这一范围。

在质心位置和侧倾力矩臂已定的情况下，使附加力矩为零的角刚度比值就已被确定，并可计算出来；反之，不管角刚度比数值有多大，在质心位置已定的情况下，仍可通过调整侧倾力矩臂的大小和方向来使车身不受附加力矩的影响。

总之，匹配角刚度，须把转向特性和车身受力两种因素综合考虑。

计算示例

独立三轴汽车，其悬挂负荷P=73500N（质心面在1、2轴之间）；各轴弹簧线刚度：c₁=255N/mm，c₂=275N/mm，c₃=265N/mm；各轴至第1轴的距离：l₁=0，l₂=2400mm，l₃=4500mm；悬挂质体质心面至第1轴的距离：l=2000mm；横向簧心距：B=1800mm。

①用式（2-8）计算系统组合线刚度，计算结果：c=770N/mm。

②用式（2-9）计算悬挂质体质心处的静变形量，计算结果：f=93mm。

③用式（2-6）计算外心距，计算结果：R₀=-10363mm（瞬心在右侧）。

④用式（2-10）计算各簧静变形量，计算结果：f₁=114mm，f₂=91.8mm，f₃=72.5mm。

⑤用式（2-11）计算质心面和各轴处的振动频率，计算结果：n₁=88.9次/min，n₂=99次/min，n₃=111.4次/min，n=97.1次/min。

⑥用式（2-15）计算各簧变形力（负荷分配），计算结果：P₁=29051N，P₂=25247.6N，P₃=19201.3N。

⑦用式（2-19）计算中性面至第1簧的距离，计算结果：a₁=2330mm，与中轴至第1轴的距离2400mm相差70mm，偏离值c₃l₃/（c₁+c₃）为107mm。

⑧用式（2-22）计算内心距，计算结果R_i=-330mm，负值说明中性面在悬挂质体质心面的右侧。

⑨用式（2-23）计算末轴与首轴的偏频比，计算结果：ξ=1.25。

⑩用式（2-28）计算整车纵向角刚度，计算结果：c_θ=2633575472N·mm/rad。

⑪用式c_αi=c_iB²/2计算各轴横向角刚度，计算结果：c_α1=413100000N·mm/rad，c_α2=445500000N·mm/rad，c_α3=429300000N·mm/rad。

⑫用式c_α=∑c_αi计算整车横向角刚度，c_α=1287900000N·mm/rad。

⑬用式（2-31）计算横向角刚度的检验值，设侧倾力矩臂e_s=1000mm，计算结果：c_αT=588000000N·mm/rad。显然，c_α＞c_αT。

⑭用式（2-33）计算纵向角刚度的检验值，设倾覆力矩臂e_l=1500mm，计算结果：c_θT=2205000000N·mm/rad。显然，c_θ＞c_θT。

⑮用式（2-34）计算转向特性总角刚度比，计算结果：λ_n=0.976。此值小于1，故属过多转向趋势。

⑯用式（2-35）计算等角侧倾角刚度比，假设各轴侧倾力矩臂均等于1000mm，计算结果：λ₁=0.35，λ₂=0.345，λ₃=0.305。

⑰用式c_αi^′=λ_ic_α计算各轴等角侧倾角刚度，计算结果：c_αl^′=450765000N·mm/rad，c_α2^′=444325500N·mm/rad，c_α3^′=392809500N·mm/rad。

由第⑪条的数值可知，一轴数值偏低，三轴数值偏高，中轴数值接近。假如各轴线刚度不能改变，那就应改变一、三轴的导向机构设计，使一轴的侧倾力矩臂相应缩短，使三轴的侧倾力矩臂相应加大。