悬架换算线刚度是悬架计算的基础，它包括的范围很广，如弹簧和轮胎的串联组合线刚度为

又如非对称钢板弹簧，若两端弹簧的线刚度为c₁、c₂，那么它们的并联组合线刚度为

各种独立悬架的换算线刚度公式是最有用的，然而它的计算公式推证起来是比较复杂的。下面仅介绍通用公式的推证，至于具体悬架，仅举一个例子，其余公式此处不予推证。

所谓独立悬架的换算线刚度，就是在车轮处，也就是在所谓杠杆比等于1处的地面上，垂直地放置一个弹簧，这个弹簧与放置在杠杆比不为1处的实际弹簧的作用相当。有人把这个假设的弹簧命名为“等效弹簧”，它的线刚度即换算线刚度。

各种独立悬架的换算线刚度公式，一般采用虚位移原理来推证。即假定悬架系统是常定的理想约束系统，该系统在主动力的作用下，平衡的充要条件是虚位移所生之元功和为零，即

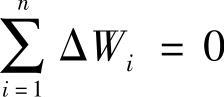
系统在外力作用下，地面相对于车身的垂直位移Δf即是“等效弹簧”的垂直变形。换算线刚度k与Δf的乘积，就是在车轮着地点作用于系统的微元力ΔP。在主动力系中，除力ΔP外，还仅有一个实际弹簧的变形力δP=cδf。c是实际弹簧的线刚度，δf是弹簧轴线方向的变形量。这是因为导向杆系的约束反力的合力通过瞬心，其功为零。而且各铰接部位刚性无摩擦，地面无滑动摩擦。因此，由虚位移原理可得

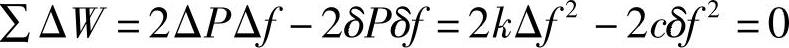
单边悬架的换算线刚度为

由式（2-26）可知，只要求出了δf及Δf与悬架结构和原簧刚度的关系，各种悬架的k值也就确定了。

例如，摆臂内交、臂销平行的双横臂独立悬架的Δf和δf结构表达式的推导如下所述（图2-18）。

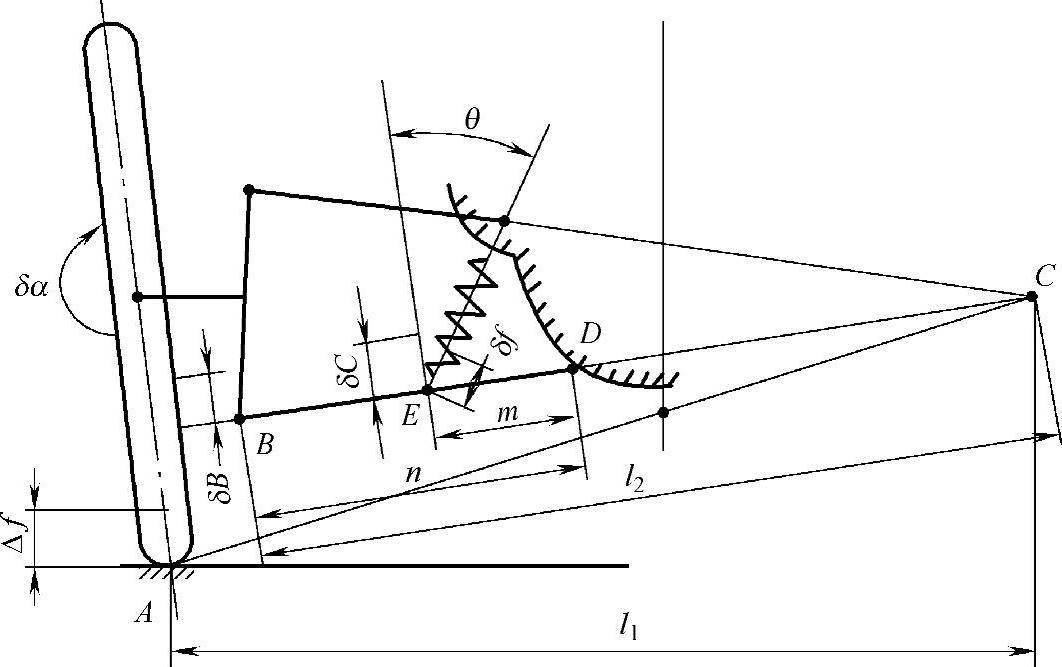
图2-18 摆臂内交、臂销平行的双横臂独立悬架

设车轮相对于车身绕瞬心C转过了一个微元角δα，那么由图2-18可知，车轮的垂直位移为(www.daowen.com)

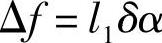
即

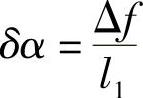
当下臂绕点D旋转时，点B的位移δB与点E的位移δE的关系为

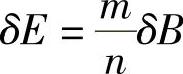
又由于点B与车轮为一整体，点C也是点B的瞬心，所以有

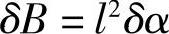
进而有

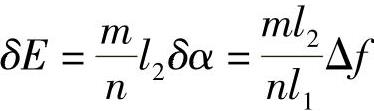
弹簧沿轴线方向的变形量为

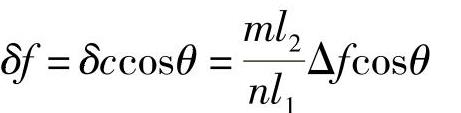
式中 θ——弹簧轴线与下臂垂线间的夹角。

将δf代入式（2-26），便得

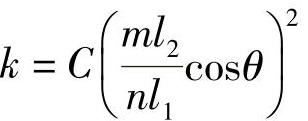
对于整桥，换算刚度k_整桥=2k。

部分悬架的换算线刚度，详见第三章第一节。