所谓多簧质量系统，是由多个弹簧并联构成的弹簧质量系统，如图2-16所示。在多簧质量系统悬挂质体质心处作用一个垂直载荷P，质体将绕着一个振动中心O（摆振轴线）振动。振动中心到悬挂质体质心面的距离R₀，便是所谓的振动中心距。知道了振动中心距，便为计算各簧（各悬架）的变形和负荷分配等打下了基础。

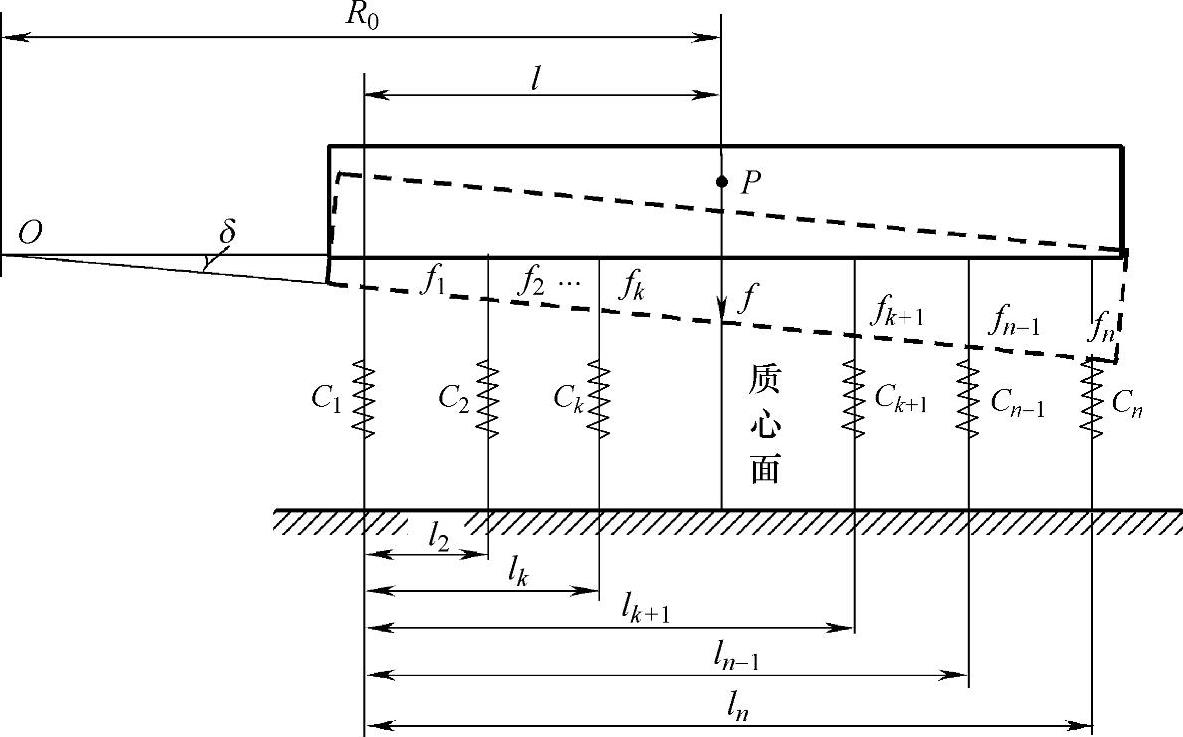
图2-16 质体绕外心倾斜振动

为建立多簧质量系统振动中心距R₀的计算方法，假定系统由刚度为c_i的n个弹簧并联组成。悬挂质体为一刚体，其质心面在第k和k+1个弹簧之间。k为从1到（n-1）之间的任意正整数。当在质心面处作用一个垂直载荷P时，悬挂质体便绕振动中心O产生一个角位移δ。此时各簧的垂直位移为f_i，质心的垂直位移为f。

由力矩平衡关系可得

由图2-16的几何关系可得

将式（2-5）变为f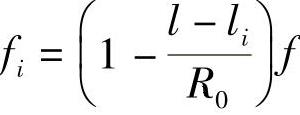，并代入式（2-4）后可得

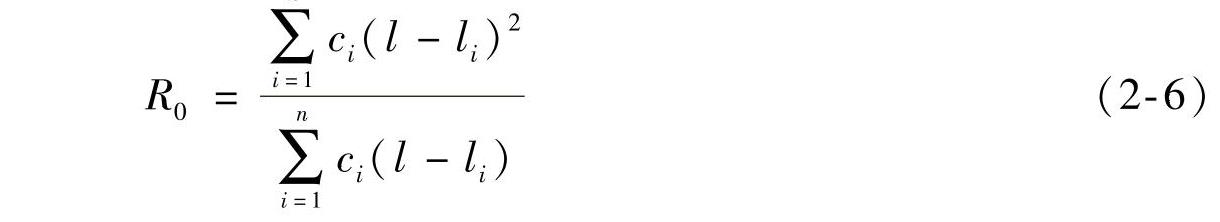(www.daowen.com)

式中 R₀——振动中心距（mm）

c_i——各簧线刚度（N/mm）；

l——质心面至第1簧的距离（mm）；

l_i——各簧至第1簧的距离（mm）。

振动中心距是系统中的固有特性参数，不受外力影响。

如果式（2-6）中的分母为零，则R₀→∞，瞬心在无穷远处。R₀→∞意味着质心面与中性面重合（见后文），此时，悬挂质体只产生平上平下的运动。

如果R₀为正值，说明振动中心在图2-16的左侧。

如果R₀为负值，说明振动中心在图2-16的右侧。

如果R₀=0，说明振动中心就在质心之上，这是一种应尽力避免的情况。作为汽车的实际情况，振动中心一般都在汽车右端车体的外侧，所以本书第1版把振动中心距称为外心距。