单横臂悬架侧倾力矩中心的求法已在图2-9中介绍，下面介绍独立柱式悬架、钢板弹簧相关悬架、纵向斜置四杆相关悬架以及内收式双横臂独立悬架等的侧倾力矩中心的求法。

1.独立柱式悬架

独立柱式悬架可以用瞬时转动中心法来求力矩中心，如图2-10所示。P₂₃是地面2与左轮3的瞬时转动中心，而左轮3与车身1的相对运动方向是垂直的，故其相对运动瞬时转动中心P₁₃必在与相对运动方向相垂直的无穷远处。因此，P₁₃和P₂₃的连线就是通过P₂₃的水平线，它与地面完全重合。同理，P₂₄和P₁₄的连线也与地面重合。因此，P₂₃、P₂₄连线上的任何一点都可能是瞬时转动中心。O点是位于中性面上且在P₂₃和P₂₄连线上的点，因此，它就是侧倾力矩中心。

2.钢板弹簧相关悬架

图2-11所示为以自身作导向机构的钢板弹簧相关悬架，它与上述柱式相关悬架有着相似的特性。

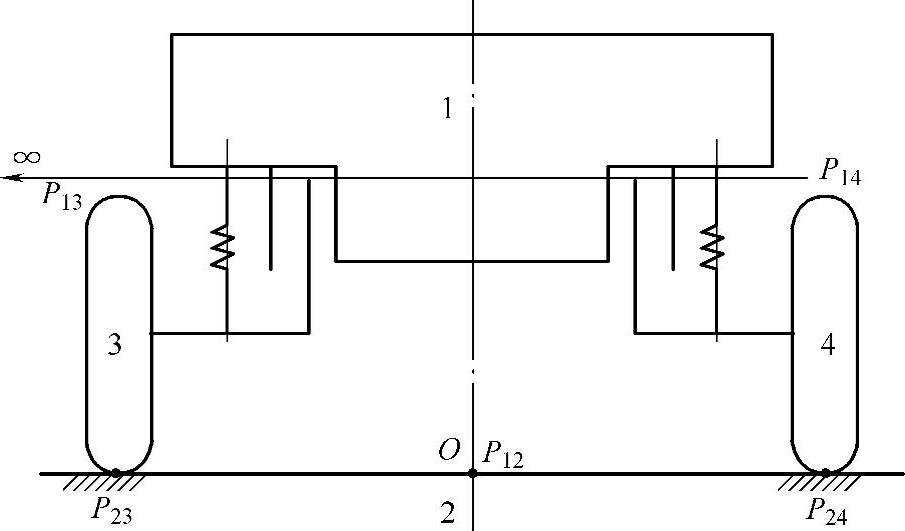
图2-10 独立柱式悬架

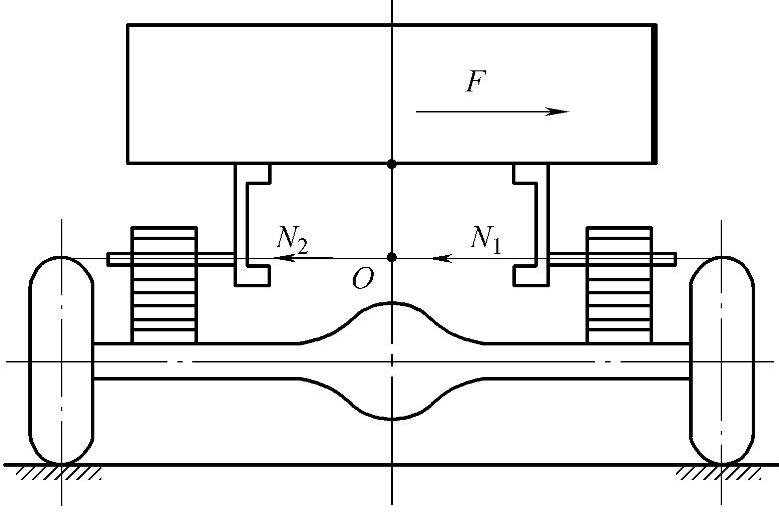
图2-11 钢板弹簧相关悬架

当离心力F作用于悬挂质体时，板簧铰链处便产生对车身的约束反力N₁和N₂。假设板簧弧高为零，N₁、N₂则水平作用于板簧，合力N=N₁+N₂，它与中性面的交点O就是侧倾力矩中心。

若板簧主片呈弧形，铰链处除水平反力外，尚有一个力矩，这使约束反力作用线略为下移。主片若呈反弓形，作用线则略为上移。

3.纵向斜置四杆相关悬架

图2-12所示的纵向斜置四杆相关悬架，其铰链都具球铰链效果。在离心力F的作用下，F是靠四杆反作用力N₁、N₂、N₃和N₄来平衡的，这四个约束反力的合力作用点就是O。注意它不是O′，只不过是O′在过车轮着地中心且垂直于x轴的平面上的投影。因为N₁、N₂合力的横向分力N′以及两纵杆的约束反力N₃、N₄所构成的力矩化简的结果（b=aN₃/N′），就使N′移至车轮正上方。

由图2-12可知，车身、车桥与两个斜杆在横向平面上构成一个“单自由度的四杆机构”。该机构的两斜边是两斜杆在横向平面上的投影。

在车身高度不变时，斜杆长短不变，此时只有一个瞬时转动中心，利用三心定理就可迅速求得瞬心就是两斜边的交点。(www.daowen.com)

若N₃、N₄在水平面和垂直面皆不平行，则须再用两次三心定理。

4.内收式双横臂独立悬架

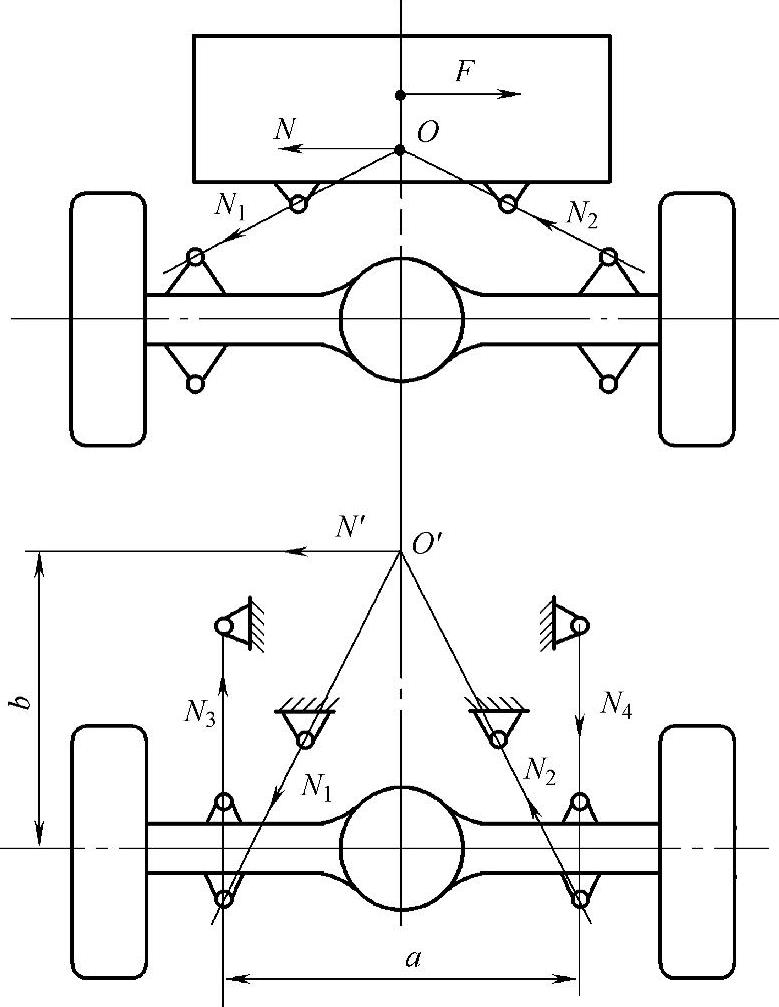
图2-12 纵向斜置四杆相关悬架

图2-13所示为内收式双横臂独立悬架，可采用三心定理来求瞬时转动中心。在左半部，车轮3与上杆4的相对瞬时转动中心是P₃₄，而上杆4与车身1的相对瞬时转动中心是P₁₄。根据三心定理，车轮3与车身1的瞬时转动中心必在P₃₄和P₁₄的连线上。

同样，下杆5与车轮3和车身1的相对瞬时转动中心分别为P₃₅和P₁₅。根据三心定理，车身1与车轮3的相对瞬时转动中心又必在P₃₅和P₁₅的连线上。因此，两条连线的交点P₁₃就是车身对左轮的瞬时转动中心。

知道了左轮对车身的相对瞬时转动中心（悬架中心）P₁₃，而且可知道车轮3对地面2的相对瞬时转动中心就是P₂₃，因而，根据三心定理，车身1对地面2的瞬时转动中心P₁₂必在P₂₃和P₁₃的连线上。

按同样的步骤可以求出，车身1对地面2的瞬时转动中心P₁₂又必在P₂₆和P₁₆的连线上。

由于横向瞬时转动中心与侧倾力矩中心的一致性，P₁₂就是侧倾力矩中心O。

如果双横臂的上下臂是水平的，则力矩中心在地平线与中性面的交点处。

如果双横臂的上下臂是外交式的，则力矩中心将钻入地平面之下，使侧倾力臂增大。

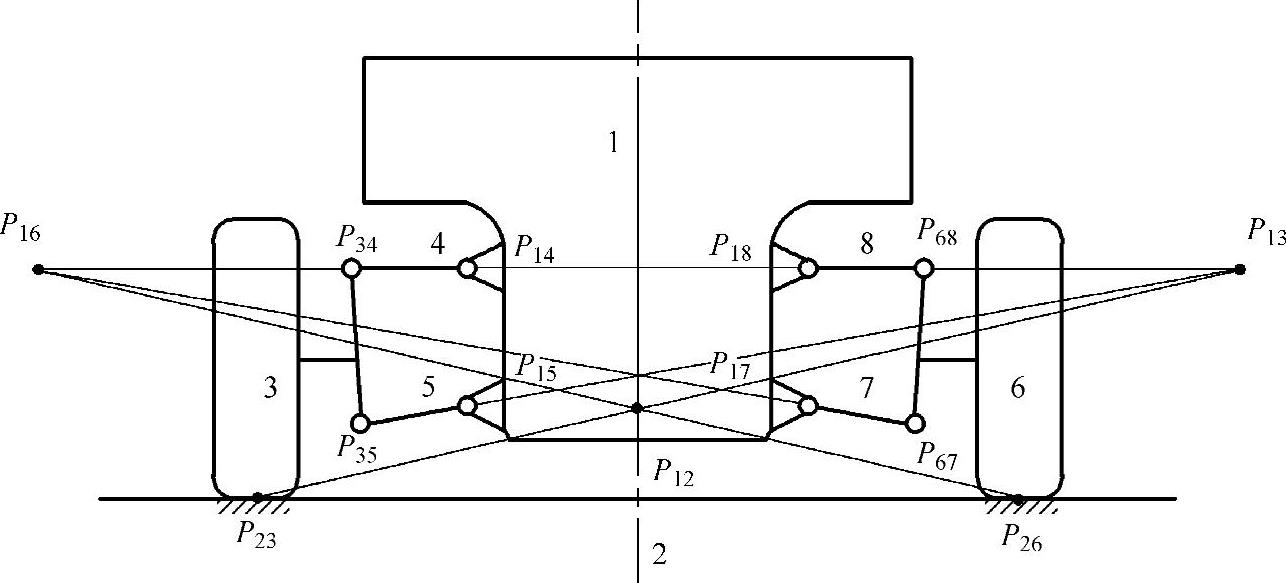
图2-13 内收式双横臂独立悬架