1.虚位移原理

假定悬架系统是常定的理想约束系统（刚性连接、无摩擦、无滑动），该系统在主动力系作用下，平衡的充要条件是虚位移所生之元功和为零，即

例如，在图2-3所示的单横臂悬架中，主动力系的力仅有ΔP和δP，轮胎和弹簧的变形分别为Δf和δf，虚位移所生之元功和为

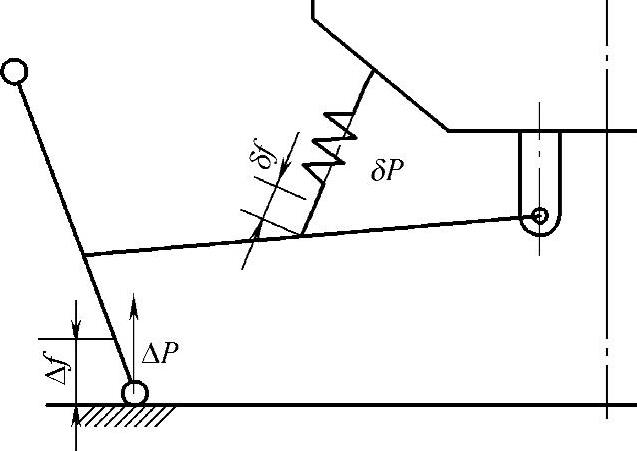
图2-3 单横臂悬架受力情况

2.等效法则

在图2-4a中，刚度为c的弹簧放在杠杆比为m/n的地方，如果在车轮着地处，也就是杠杆比m/n=1的地方放置一个刚度等于k的弹簧（图2-4b）来取代原弹簧，其力学性质不变，效果不变。这个后放置上去的弹簧，就叫做等效弹簧（当量弹簧）。

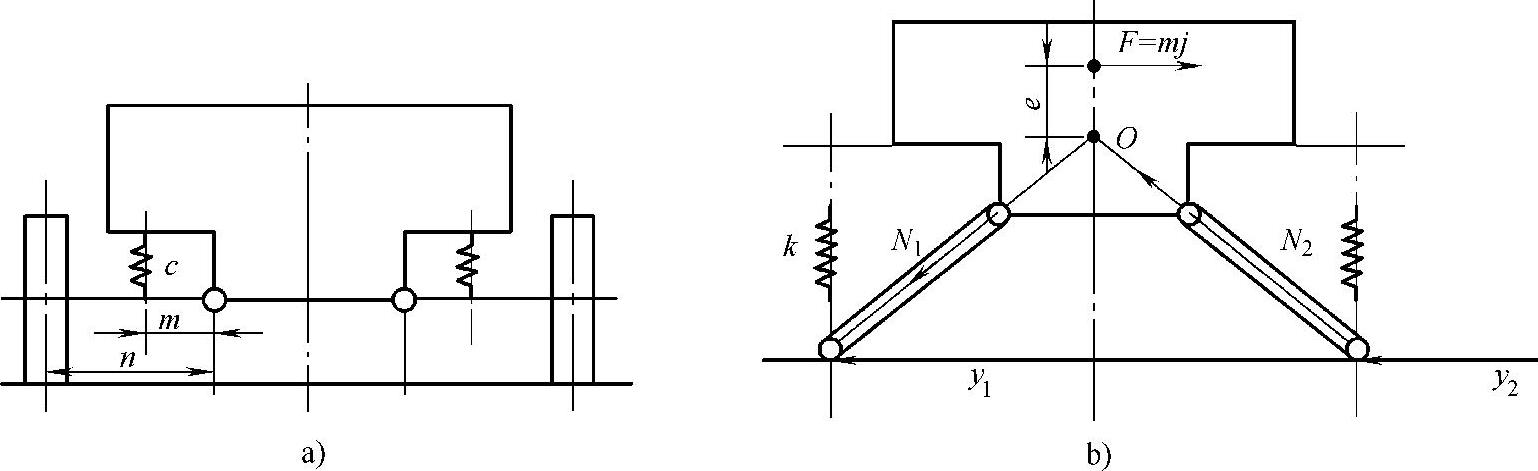
图2-4 等效弹簧

3.硬化公理

由数个可以相对运动的构件组成的系统，在平衡的瞬时，可以把它们看成是一个刚性的整体。所谓刚性整体，就是在此刻构件间不存在相对位移。这个公理对于寻求悬架中心和简化机构是很有用处的。下面举例说明。

【例1】 双纵臂导向机构

双纵臂导向机构在受到制动力或驱动力后，上、下杆对车身都有作用力，其方向必都沿着各自的杆向，如图2-5所示。悬架对车身作用力的合力，也就是上、下杆对车身作用力的合力，必通过两杆延长线的交点，也就是纵向悬架中心C。根据硬化公理，在平衡的时刻，可以把上下杆和车轮一起看成是一个刚性的整体。而点C和车轮着地中心E是这个刚体上仅有的两个受力点。显然，这两点处的合力大小相等、方向相反，作用线就是这两点的连线（即两个瞬时转动中心）。合力的大小可以由它在水平方向的投影等于该轮的制动力或驱动力求得。

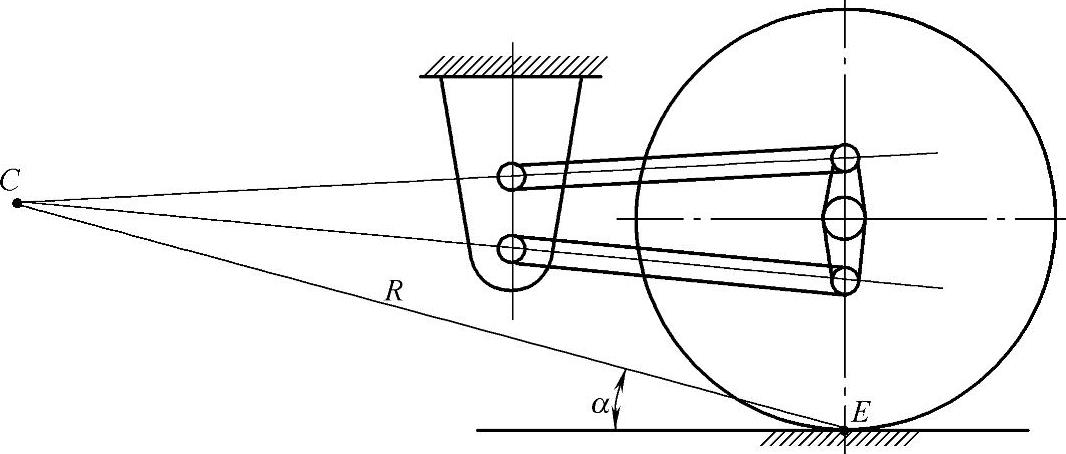
图2-5 双纵臂的悬架中心

由上述可知，此处的双纵臂悬架已被化为一个等价的单纵臂悬架了。在这里我们把CE长度R称为“推杆”，把夹角α称为推杆角。

如果两杆平行，则悬架中心在无穷远处，“推杆”线与地面重合。

【例2】 双横臂导向机构

双横臂摆臂轴销线相交于前轮后方，制动力P_τ作用于车轮着地中心E，上、下臂的约束反力N_u、N_d的方向与轴销线相同，N_u、N_d的合力N必通过轴销线的交点——纵向悬架中心C，如图2-6所示。

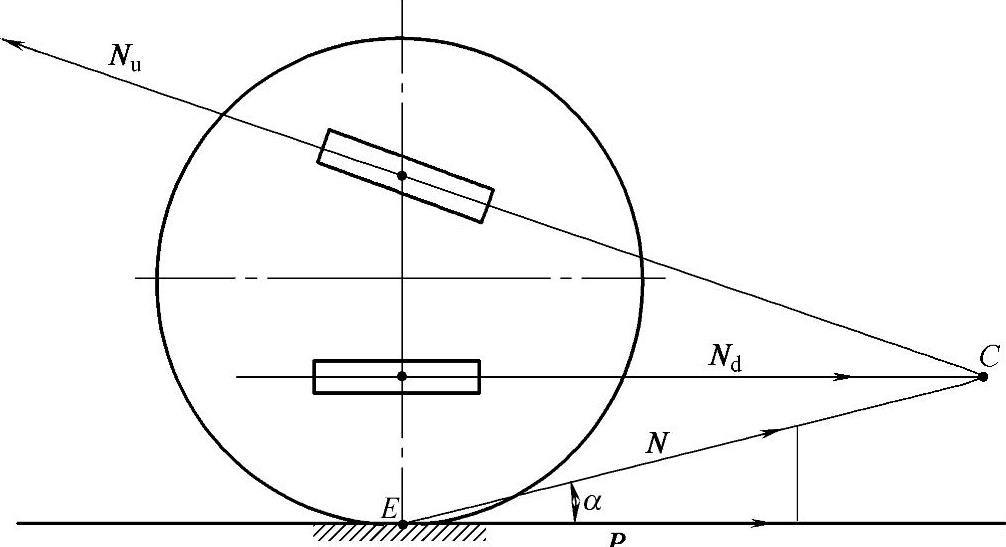
图2-6 双横臂纵向悬架中心

根据硬化公理，在平衡的时刻可将轴销和车轮一起看成一个刚性的整体。而C、E两点是这个“刚体”上仅有的两个作用点，显然C、E两点处的合力N大小相等，方向相反，作用线就是E、C的连线，它在水平方向上的投影等于制动力P_τ。由此可知，双横臂导向机构已被化为一个等价的单纵臂悬架了。

4.力矩中心说

郭孔辉院士曾提出“任何形式的悬架系统，都有一个侧倾力矩中心，它就是导向杆系约束反力的合力与中性面（参见本章第二节）的交点”。侧倾力矩臂就是侧倾力矩中心高度与悬挂质体质心高度的差。这个力矩臂可为正，可为负，还可为零。

整车总的侧倾力矩中心，应是前、后悬架导向杆系约束反力的总合力与中性面的交点。若将前、后悬架约束反力的总合力在此点分解为水平分力和垂直分力，则水平分力与整车惯性力大小相等，方向相反，构成侧倾力矩；而垂直分力通过悬挂质体质心，它只引起车身上下移动而与横向倾斜无关。

整车力矩中心应在前后悬架力矩中心O₁、O₂的连线上，如图2-7所示。

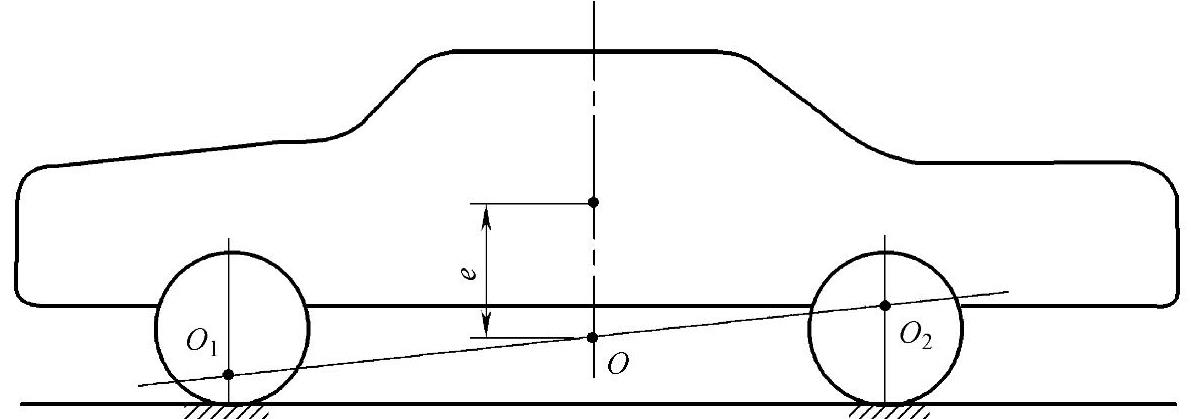
图2-7 整车力矩中心

针对二轴汽车，这个结论是正确的，但针对多轴汽车，则需进一步研究。

多轴汽车似乎也应该有一个共同的侧倾轴线，但各悬架的侧倾力矩中心是否都落在这一条轴线上呢？显然值得研究！

对于三轴以上的汽车，它们之间就不是统一协调的，而是超静定的、矛盾的，车身侧倾时，只能以车身和弹性元件以及杆件等的变形来作为统一条件。在同一辆汽车上，由于各车轴悬架的侧倾力矩中心在其高度上很有可能不在一条直线上，这就意味着没有形成一条统一的侧倾轴线，似乎车身无法侧倾！然而，此时各悬架的负荷将发生改变，从而迫使弹性元件的变形量发生改变，导向机构的位置也将发生改变，进而调整了各悬架侧倾力矩中心的高度，以使矛盾获得统一。此外，车身为保持等角侧倾，车身整体以及相关元件也将产生变形，这正是车辆转弯时，发出“吱吱呀呀”声响的原因。

多轴汽车的侧倾力矩臂可以利用作用于各悬架的侧倾力矩之和∑m_ije_i（j为侧向加速度）等于整车的侧倾力矩mje来求得一个当量力矩臂，即

(www.daowen.com)

式中 e、e_i——整车和各悬架的力矩臂；

m、m_i——整车和各悬架的悬挂质体质量。对于二轴汽车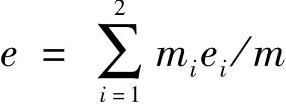，。若按几何关系，还可求得二轴汽车整车侧倾力矩臂的计算公式为

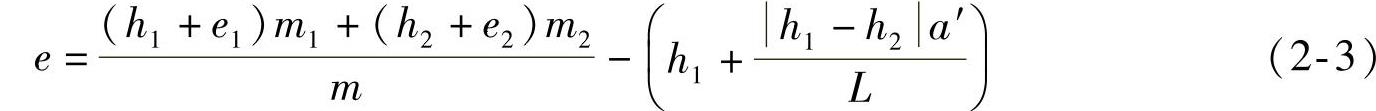
式中 h₁、h₂——前、后悬架力矩中心离地高度；

a′——悬挂质体质心至前轴的距离；

L——轴距。

式（2-2）和式（2-3）的计算结果是完全一致的。这也说明，侧倾轴线既通过悬架的力矩中心，也通过整车的力矩中心。

作为设计者，可以将多轴汽车各悬架的力矩中心设计到一条侧倾轴线上，或者近于一条轴线上，以使车身侧倾运动时，缓和矛盾，减少变形。

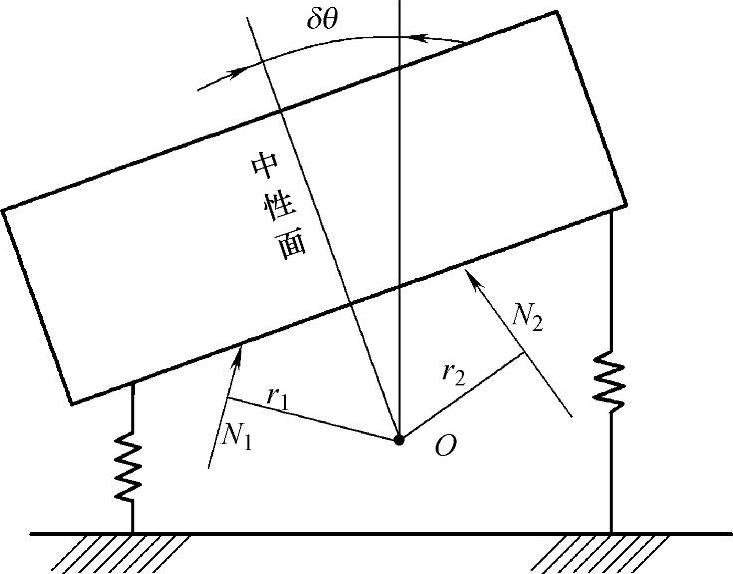
图2-8 瞬心和力矩中心

5.“二心”一致性

“二心”是指瞬时转动中心和力矩中心，所谓“二心”一致性就是指在单自由度下，如果悬挂质体具有一个绝对瞬时转动中心，而且位于中性面上，那么力矩中心必在绝对瞬时转动中心上。

假设悬架为理想约束，如果在某一瞬时悬挂质体绕瞬时转动中心O旋转一个微小位移δθ（图2-8），那么导向杆系约束反力所生之元功和为零，即

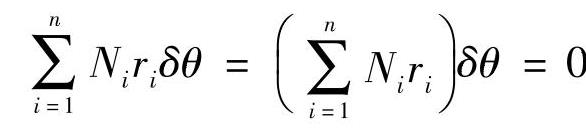
式中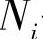——某一约束反力；

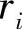——N_i到瞬时转动中心的距离；

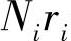——第i个约束反力对瞬时转动中心的力矩；

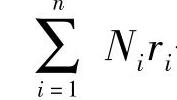——n个约束反力对瞬时转动中心的力矩和。

由力学可知，所有分力对某一点的力矩和，必等于其合力N对该点的力矩。设合力到瞬时转动中心的距离为r，那么便有

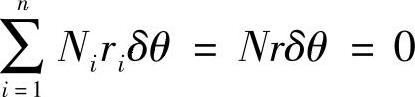
由于N和δθ不为零，故唯一能使虚功为零的条件就是r=0，即约束反力的合力通过瞬时转动中心。

由前述可知，侧倾力矩中心就是导向杆系约束反力的合力与中性面的交点，若瞬时转动中心在中性面上，则这个瞬时转动中心就是导向杆系与中性面的交点，即侧倾力矩中心。假设自由度不为1，瞬时转动中心就不止1个，那么只有位于中性面上的那个可能的瞬时转动中心才是侧倾力矩中心。

6.三心定理

力学中的“三心定理”对于求解复杂导向机构的力矩中心是很有用处的。它是通过求瞬时转动中心的办法来求取力矩中心的。

“三心定理”——三个杆件的三个相对瞬时转动中心必排列在一条直线上。

图2-9所示为一个单横臂悬架，由图可知，车轮3与地面2的“瞬心”是P₂₃，车身1与车轮3的瞬心是P₁₃，由“三心定理”便知，车身1与地面2的相对瞬心P₁₂必在P₂₃和P₁₃连线的延长线上。

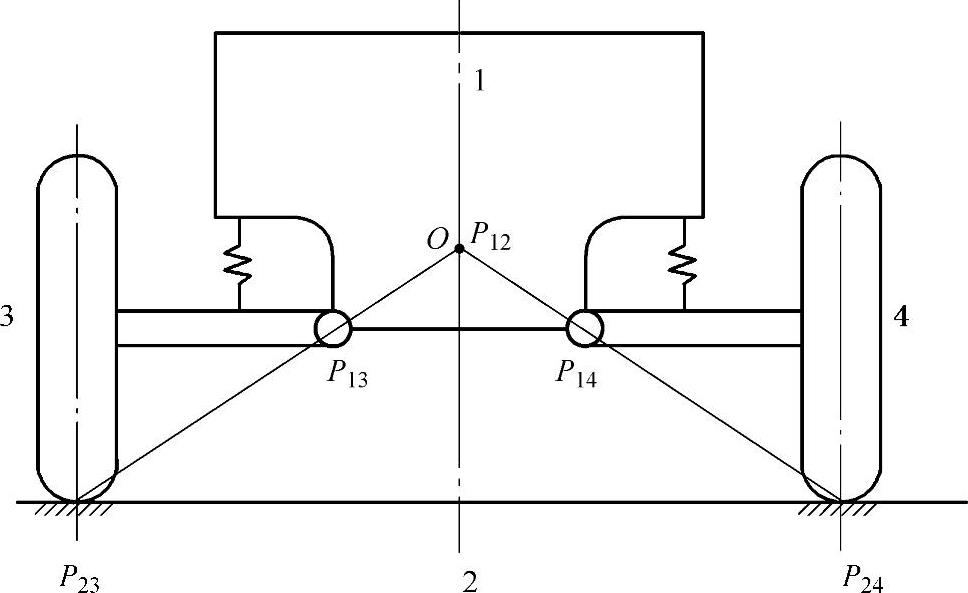
图2-9 单横臂悬架

同理可知，P₁₂又必在P₂₄和P₁₄连线的延长线上。也就是说，P₁₂就是车身与地面的瞬时转动中心。根据“二心”一致性，P₁₂就是力矩中心O。

值得说明的有如下两点：

①根据三心定理，在多数情况下可以较为容易地找到瞬心，而“二心”一致性则又可以判定它为力矩中心。然而这是有条件的，就是单自由度，是一个瞬心的假设，是瞬心必须在中性面上。然而严格地说，车身对称面及质心面往往不与中性面重合。因此，利用三心定理寻找力矩中心，虽然较为方便，但不一定准确。

“导向杆系约束反力的合力与中性面的交点就是力矩中心”的力矩中心说，有时虽较麻烦，但它较为准确，特别是有时它反而还简单。所以两种方法，均可酌情选用。此外，从设计者的角度出发，应尽可能在横向上使中性面落在质心面和几何对称面上。

②图2-9中的P₁₂、P₁₃、P₁₄、P₂₃和P₂₄这些点，必须在同一平面上，也就是必须落在过车轮着地中心P₂₃和P₂₄，且垂直于x轴的平面上，否则所谈理论是不成立的。

有了中性面理论以及相关的原理、法则和定理，我们便可以分别推求不同悬架的力矩中心了。