无缝线路的特点是轨条长，当轨温变化时，钢轨要发生伸缩，但由于有约束作用，不能自由伸缩，在钢轨内部要产生很大的轴向温度力。

当钢轨因温度变化Δt℃而自由伸缩时，其伸缩量为

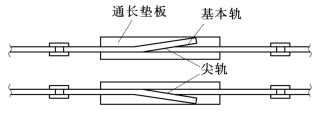
图5-47　尖轨接头

式中 α——钢轨的线膨胀系数，取11.8με/℃ （或11.8×10-6ε/℃）；

l——钢轨长度，m；

Δt——轨温变化幅度（或称轨温差），℃。

如果钢轨因受阻力不能随轨温变化而自由伸缩时，则将在钢轨内部产生温度应力。由虎克定律可得温度应力为

式中 E——钢的弹性模量，E=2.1×105 MPa；(www.daowen.com)

εt——钢轨的温度应变。

将E、α的值代入式（5 2），则

一根钢轨中的温度力为

式中 F——钢轨的断面积，cm2。

由此可得知：

（1）在两端固定的钢轨中所产生的温度力，仅与轨温变化幅度有关，而与钢轨本身长度无关。因此，从理论上讲，钢轨可焊成任意长，且对轨内温度力没有影响。控制温度力大小的关键是如何控制轨温变化幅度Δt。

（2）对于不同类型的钢轨，同一轨温变化幅度产生的温度力大小不同。对于75kg/m、60kg/m、50kg/m钢轨，如轨温变化1℃所产生的温度力分别为23.6kN、19.2kN、16.3kN。

（3）无缝线路钢轨伸长量与轨温变化幅度Δt和轨长l有关，与钢轨断面积无关。