岩石在外力作用下所表现出的性质，即为岩石的力学特性。在外力作用下，岩石首先产生变形，随着外力的不断增加，达到或超过某一极限值时，便产生破坏。具体到岩石在外力作用下呈现何种性状，则取决于其成分、结构、受力条件以及赋存条件等。研究岩石的力学性质，主要从岩石的变形、流变、强度等性质入手。

一、岩石的变形特征

和其他材料一样，岩石受力时会产生变形。如果按其应力—应变关系，可将其变形性状分为弹性变形和塑性变形两种。固体力学中定义弹性变形，是指物体在外力作用下产生变形，当撤去外力后能够立即恢复到原有的形状和尺寸的变形；塑性变形是指物体受力变形，除去外力后变形不再恢复的变形，又称永久性变形或残余变形。下面将主要研究岩石单向受压情况下的变形特征。

岩石的变形规律，可通过外力作用下的变形参数说明，所以有必要先了解岩石的应力-应变关系。首先着重研究简单的单向受压条件下的应力-应变关系。

1. 岩石的应力-应变曲线

对一定形状（圆柱体、长方体等）的岩石试件，用材料试验机按一定时间间隔施加单向压力，测量加压过程中各级应力及相应的轴向应变（e）和横向应变（d）值。并由此可以计算出体积应变值（εV）和绘出以压力（σ）为纵坐标、各类应变为横坐标的应力-应变曲线。据大量实验表明，在单向压力作用下，典型的应力-应变全过程曲线（见图 6.1），大致可分为5个阶段：

（1）O—a 段，微裂隙及孔隙闭合阶段。σ-εl曲线呈上凹型，表明裂隙、孔隙压密开始较快，随后渐慢（斜率逐渐增大）；体积随压力增加而减小，即εv为正值，σ-εd曲线陡。

（2）a—b 段，可恢复弹性变形阶段。σ-εl曲线近呈直线，相应于 b 点的应力值称为比例极限（或弹性极限），变形在很大程度上是可恢复的弹性变形。

图6.1 岩石单轴压缩应力-应变全过程曲线

σ—应力；ε1—轴向应变；εd—横向应变；εv—体积应变

（3）b—c 段，部分弹性变形至微裂隙扩展阶段。这一阶段曲线由 b 点开始偏离直线，σ—εv曲线最为明显，其斜率随σ的增大而变陡，直至变负；εv近线性增长，至 c 点岩石压密至最密实状态，体积由压缩转为膨胀，相应于c点的应力值为屈服极限。

（4）c—d 段，非稳定裂隙扩展至岩石结构破坏阶段。σ-εl曲线斜率迅速减小，岩石体积膨胀加速，变形随应力迅速增长，微裂隙迅速增加、扩展形成局部的拉裂或剪切面，最终导致岩石结构完全破坏。至d点，应力达到最大值，称峰值强度或单轴极限抗压强度。

（5）d 点以后的阶段。岩石过 d 点后，虽然内部结构完全破坏，但岩石仍呈整体，仍有较小的承载能力，随变形不断增加，应力降到某一稳定值，即残余强度，其大小实际上等于破碎块体之间的摩擦阻力。

以上通过对岩石应力-应变关系阶段的划分，可得到4个特征应力值，即比例极限、屈服极限、峰值强度和残余强度。但这是典型化了的曲线，反映了岩石的一般变形习性。由于岩石成分、结构不同，其应力-应变关系也不尽相同，所以并非对所有岩石都可以明显划分出这5个变形阶段。

1965年，美国学者 R·P·米勒根据对28种岩石的实验研究。把在单向压力作用下的应力-应变曲线归纳为6种类型（见图6.2）。

类型Ⅰ为玄武岩、石英岩、辉绿岩、白云岩及坚硬石灰岩等的特征变形曲线，表现为近于直线的特点，直到发生突发性破坏；类型Ⅱ是较软且裂隙少的岩石（如石灰岩、粉沙岩和凝灰岩等）常呈现的变形曲线，开始为直线，末端出现非弹性屈服段；类型Ⅲ为坚硬且裂隙发育的岩石（如沙岩、花岗岩等）在垂直微裂隙方向加荷时常具有的变形曲线，开始为凹曲线，然后转变为直线；类型Ⅳ和Ⅴ（塑-弹-塑性的）为S曲线，岩性较软且有微裂隙者，如片麻岩、大理岩和片岩等常具有这种变形，曲线中段的斜率大小与岩性软硬程度有关；类型Ⅵ（弹-塑-蠕变性的）是岩盐和其他蒸发岩的特征变形曲线，开始为直线，很快变成非线性和连续缓慢的蠕变形。

图6.2 单轴压缩岩石直至破坏的典型应力-应变曲线

Ⅰ—弹性的；Ⅱ—弹-塑性的；Ⅲ—塑-弹性的；Ⅳ—塑-弹-塑性的；Ⅴ—塑-弹-塑性的；Ⅵ—弹-塑-蠕变性的

2. 岩石的变形参数指标

根据各种类型的应力-应变曲线，可以确定岩石的变形指标。在工程实践中，最常用的岩石变形指标有弹性模量E和泊松比μ。弹性模量E是指单轴压缩条件下轴向压应力（σ）与轴向应变（ε）之比。当轴向的应力-应变曲线呈直线型时（见图 6.3），则数值上等于直线的斜率。应力-应变关系不呈直线时，岩石的变形特征可以用以下几种模量说明（见图6.4）。

图6.3 应力与应变为直线关系时确定E的方法

图6.4 岩石的各种模量的确定

初始模量，是应力-应变曲线在原点切线的斜率，即

切线模量，是对应于曲线上某一点M的切线的斜率，即

割线模量，是曲线上某一点M与坐标原点连线的斜率，即

岩石的另一个重要的变形指标是泊松比（μ），指岩石在单向受压时，横向应变与轴向应变之比，即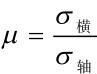。一般来说，由于这一指标是由弹性理论引入的，故只适用于岩石弹性变形的阶段，当岩石受压内部出现破裂时，泊松效应失效。

3. 循环荷载条件下的岩石变形特征

岩石在循环荷载作用下的应力-应变关系，随加荷方法及卸荷应力的不同而异。当在同一荷载条件下对试件加荷、卸荷时，如果卸荷点（P）的应力低于岩石的弹性极限（σA），则卸荷曲线将基本上沿加荷曲线回到原点，表现为弹性恢复（见图 6.5）。但应注意，虽然大部分弹性变形在卸荷后可很快恢复，但小部分（约 10%～20%）必须经一段时间后才可恢复。这种现象称为弹性后效。如卸荷点（P）的应力高于弹性极限时，则卸荷曲线从原来的加荷曲线偏离出来（见图6.6）。如果加荷、卸荷反复多次，可得到图6.7所示的应力-应变曲线。当应力在弹性极限以内时，每次加荷曲线与卸荷曲线均不重合，并围成一个环形面积，称为回滞环或塑性滞环。当每次卸荷后，再用较大荷载加压，则曲线沿着单调加荷曲线上升，其形状类似于连续加荷情况［图 6.7（a）］，说明反复受荷过程并未改变岩石变形的基本习性。当应力在弹性极限以外的某一较高应力下反复加荷卸荷时，将导致变形进一步增加，直至破坏［见图6.7（b）］。破坏时的应力低于峰值强度，通常称为疲劳强度。

图6.5 卸荷点在弹性极限点以内的应力-应变曲线

图6.6 卸荷点在弹性极限点以外的应力-应变曲线

图6.7 反复加荷、卸荷时的应力-应变曲线

二、岩石的流变特性

流变是指物质在外部条件不变的情况下，应力或应变随时间变化而变化的现象。

岩石流变性主要包括以下几个方面：蠕变、松弛、流动特征和长期强度。目前，随着工程规模日益增大，有关岩体的问题越来越复杂，对精度的要求越来越高，岩石流变问题也成为十分重要的问题，特别是岩石的蠕变特性和长期强度，它们与岩体的工程变形和稳定性密切相关。

岩石在恒定应力作用下，变形随时间延续而不断增长的现象称为岩石蠕变。对一组岩石试件施以大小不同的恒定荷载，测定各试件在不同时间的应变值，可得到图 6.8 中的一组蠕变曲线。由图可见，岩石的蠕变曲线因恒定荷载的大小不同可分为两种类型：

（1）趋于稳定的蠕变——在较小恒定荷载作用下，变形随时间增长，但变形速率随时间递减，最终趋于稳定。如图6.8中的 a 曲线。

（2）非趋于稳定的蠕变——当岩石所受恒定荷载超过某一极限时，变形随时间的增长而不断增加，最终导致破坏。如图6.8中的凸曲线。

因为蠕变最终可导致破坏，所以必须引起重视，以便切合实际地评价岩石变形及其稳定性。根据蠕变曲线，可将蠕变过程划分为以下四个阶段（见图6.9）。

图6.8 岩石的蠕变曲线

图6.9 岩石的蠕变阶段曲线

①—瞬时应变；②—初始蠕变阶段；③—等速蠕变阶段；④—加速蠕变阶段

（1）瞬时变形阶段：即荷载一加上即发生的变形（如图6.9中①）。

（2）初始蠕变阶段：又称阻尼蠕变，应变ε最初随时间增长较快，但增长速率随时间逐渐降低，曲线呈下凹形（如图6.9中②）。

（3）等速蠕变阶段：应变随时间近于等速增长，曲线呈近直线形（如图6.9中③）。

（4）加速蠕变阶段：应变速率迅速增长，直至岩石破坏（如图6.9中④）。

任何一个蠕动变形阶段的持续时间都取决于岩石类型、荷载大小及温度等因素，其ε- t曲线形状也会因此有所差异。为研究岩石蠕变规律及时效性，常把岩石材料抽象成一系列弹簧、阻尼器及滑块等组成的单元系统，用它们之间的不同组合代表不同属性岩石来研究其蠕变特性，以建立起不同类型岩石的蠕变数值模型和计算其蠕变变形量，这种方法称为蠕变模型法。在此我们仅给出岩石蠕变变形经验公式

ε=εe+ε(t)+Mt+εT (t) 　 （6.4）(www.daowen.com)

式中 εe——瞬时变形；

ε (t)——初始蠕变；

Mt——等速蠕变；

εT(t) ——加速蠕变。

对于前两阶段的蠕变，很多学者得出了不同的经验公式，如康特雷勒（Cottrell）的幂函数

ε (t)＝Atn（A、n，为常数，O＜n＜1）

格里格斯（Griggs）的对数函数

ε＝εT＋Blgt＋Dt（B，D 为常数）

伊文斯（Evans）的指数函数

ε＝A [1－exp(B－Ctn)]（A，B，C 为常数，n＝0.4）

对于加速蠕变的简单公式，尚在研究之中。

三、岩石的强度

岩石在外力作用下，当达到或超过某一极限时，便发生破坏。其破坏类型可分为拉断破坏和剪断破坏两种基本形式。通常把岩石抵抗外力破坏的能力称为强度，因为外力性质不同又可分为抗压强度、抗拉强度及剪切强度等。

1. 岩石的抗压强度

岩石单向受压时能承受的最大压应力即单轴抗压强度，简称抗压强度，即

σc＝P/A

式中 σc——抗压强度（MPa）；

P ——岩石试件受压破坏时的荷载（N）；

A——试件断面面积（mm2）。

岩石的抗压强度是反映岩石力学性质的主要指标之一。它被广泛应用于岩体工程分类、建材选择及工程岩体稳定性评价计算中。实验证明岩石的抗压强度受一系列因素影响与控制，这些因素包括两方面：一是岩石自身的因素，如矿物组成、结构构造及含水状态等；另一方面是实验条件，如试件形状、大小以及加工精度、加荷速率等。

2. 岩石的抗拉强度

岩石试件单向受拉时所能承受的最大拉应力即为岩石的抗拉强度。岩石的抗拉能力较低，易被拉断而破坏，所以抗拉强度是一个非常重要的岩石力学指标。

测量岩石抗拉强度的方法有直接拉伸法和间接拉伸法两种。由于直接法试件制备困难、实验技术复杂，故多采用间接法，以劈裂法和点荷载实验最为常用。

劈裂法（见图 6.10），以一定加荷速率对试件加压，直至破坏，并按下式计算岩石的抗拉强度：

图6.10 劈裂法试验装置

式中 σt——岩石抗拉强度（MPa）；

Pt——试件破坏荷载（N）；

D ——试件直径（mm）；

l ——试件长度（mm）。

因为岩石是一种多空隙材料，而抗拉强度受空隙特别是裂隙的影响远比抗压强度大，而且拉应力条件下，仅有内聚力起作用（压应力条件下还有内摩擦阻力起作用），所以岩石的抗拉强度远远低于抗压强度。

测定岩石抗拉强度的方法有材料力学法、圆形薄片法、劈裂法（巴顿法）。但由于制样困难和试验技术复杂，并存在不少问题需要进一步解决，因此目前除有条件者外，一般利用它与抗压强度的比例关系，间接确定（表6.1、表6.2）。

表6.1 常见岩石的抗压强度值（σc）、抗拉强度值（σt）

表6.2 某些岩石抗拉强度和抗压强度间的经验关系

3. 岩石的剪切强度（τ）

岩石受剪切力作用时抵抗剪切破坏的最大剪应力，称为剪切强度，由内聚力 C 和内摩擦阻力σtan φ组成。按实验方法不同，可以分为3种剪切强度：

（1）抗剪断强度：在一定法向应力作用下，沿预定剪切面剪断时的最大剪应力。它反映了岩石的内聚力和内摩擦阻力和的大小（图6.11），即

τφ=σtanφ+ C

图6.11 岩石抗剪断试验示意图

（2）抗剪（摩擦）强度：指在一定法向应力作用下，沿已有破裂面再次剪坏时的最大剪应力。它反映了内摩擦阻力的大小（见图6.12），即

τφ=σtan φ

图6.12 岩石抗剪（摩擦）试验示意图

（3）抗切强度：指法向应力为零时，沿预定剪切面剪断时的最大剪应力。它反映了岩石的内聚力大小（见图6.13），即

τφ=C

通常用来测定岩石的抗剪断强度的方法有直剪法、变角剪切及三轴剪切等实验方法。实验表明，各类岩石的内摩擦角多在30°～60°，内聚力多在1～50 MPa之间变化。

图6.13 岩石抗切（断）试验示意图

以上对岩石的变形、流变和强度做了简单介绍，其中变形和强度只介绍了单向应力条件下的岩石的性状，但作为建筑物地基或建筑物环境的工程岩体，经常承受包括围压在内的三向应力的作用，为此研究岩石在三向应力作用下的变形和强度非常重要。