1）基本概况和分析模型

主索的顶端和底端的水平距离为32m，落差为24m，斜向距离为40m。4根主索通过节点板顺次连接，总原长为4×10.21m＝40.84m，下拉索挂在节点板上（图5-37）。导索顶端和底端的标高分别比主索的高1.0m，其总原长取值与主索的相同。主索节点板与导索之间连接有1m长的吊杆。

单元划分：将牵引索和4根主索分别划分为10个等原长的单元来模拟松垂拉索；导索与主索对应划分为4段，每段划分为一个单元，由上至下标号为A、B、C和D；吊杆划分为一个单元。考虑每根吊杆下有节点板、下拉索、手拉葫芦等荷载，设吊杆受竖直向下的集中力F＝4kN，初始分析模型见图5-38所示。

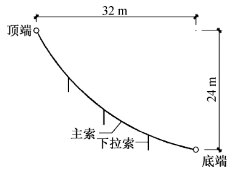
图5-37　索网结构示意图

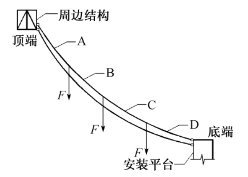
图5-38　初始分析模型

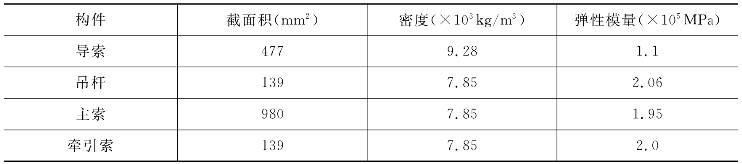
主索为7φs21.6钢绞线束，导索采用1根6×37S＋FCφ36钢丝绳，牵引索采用1根φs 15.24钢绞线，构件力学参数见表5-1所示。

表5-1　构件力学参数

采用ANSYS有限元软件，建立整体有限元模型，构件均采用Link 8杆单元。基于该软件二次开发平台编制“NDFEM”法找形分析程序，设定分析参数和收敛标准：单次动力分析时间步数允许最大值［Nts］＝5，单个时间步动力平衡迭代次数允许最大值［Nei］＝50，初始时间步长ΔTs（1）＝0.5s，时间步长调整系数Cts＝1.2，动力平衡迭代位移收敛值［Uei］＝0.005mm，位形更新迭代位移收敛值［Uci］＝2mm。

2）牵引滑移过程分析工况

基于文献［44］的思路，串联拉索沿导索空中累积滑移安装的计算过程与施工过程是相逆的，即计算分析的初始状态为施工完成状态，然后按照逆向的顺序放长牵引索，使主索沿导索向下滑移，在此过程中逐一计算施工过程各阶段的力学状态。牵引滑移过程分析工况见表5-2所示，从工况9向工况1依次分析，前个收敛的工况模型作为下一个工况分析的初始模型。

表5-2　牵引滑移过程分析工况

3）调整导索单元原长策略的分析效率对比

为模拟滑轮移动，位形迭代分析中调整导索单元原长。策略一和三分别是策略二和四在λ＝1时的特例，因此基于工况9，Ru＝0.004，Rl＝0.0 004，对比策略二和四在不同λ值下的总动力平衡迭代次数∑Nei、总时间步数∑Nts和位形更新次数Nci，分析结果见表5-3和图5-39所示。

表5-3　调整导索单元原长策略的分析效率对比

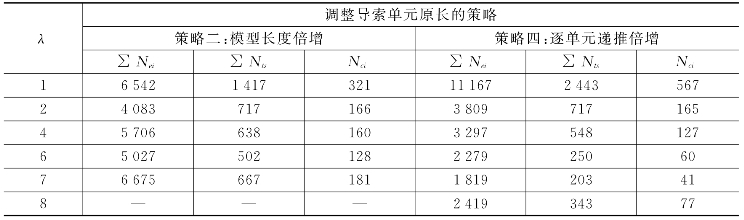
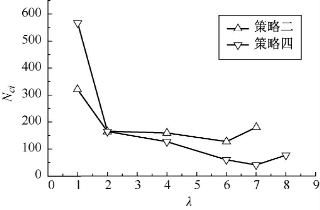
图5-39　参数对比下Nci变化曲线

由分析结果可得：

（1）当λ＝1时，策略一优于策略三。

（2）当λ＞2时，策略四优于策略二。

（3）增大λ值，大大提高了分析效率，但λ取值过大，则动力平衡迭代不易收敛，降低了分析效率。

（4）表中λ＝7时的策略四分析效率最高。(www.daowen.com)

4）不同导索原长的牵引滑移过程分析对比

设定不同的导索原长，对比分析其对牵引过程状态的影响。设导索原长分别等同于主索原长（S＝40.84m）、导索端点距离（S＝40m）及两者中间值（S＝40.42m）。调整导索单元原长采用策略四——“逐单元递推倍增”，设参数λ＝7，Ru＝0.004，Rl＝0.0 004。

经分析，导索原长S＝40.42m时各工况的位形和导索单元模型长度分别见图5-40和图5-41，可见：随牵引索原长逐渐缩短，主索沿导索累积向上滑移，上部导索单元A的长度基本呈线性减小，中部单元B的变化较小，下部单元C和D的长度增大。

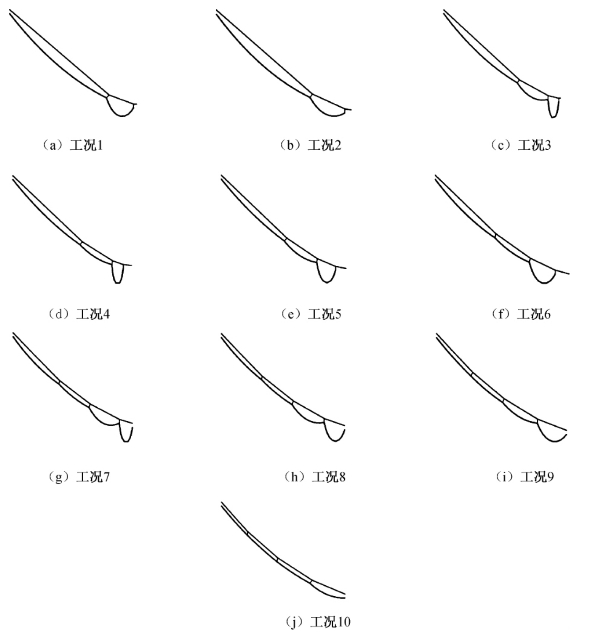
图5-40　导索原长S＝40.42m的静力平衡态位形

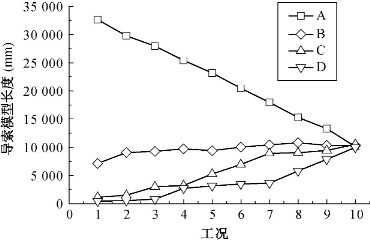
图5-41　导索原长S＝40.42m的导索单元模型长度变化曲线

对比导索三种原长下前3个工况的位形（图5-40、图5-42和图5-43），可见导索原长较长（S＝40.84m）时，起始工况的导索下端线形更加平缓，甚至可能出现下凹，不利于滑移，因此从导索线形方面来说，起始工况是最不利的，导索原长不宜过长且不应超过主索原长。

在不同导索原长条件下，对比导索和牵引索的拉力（表5-4、表5-5、图5-44和图5-45），经分析结果可得：

（1）随牵引过程，导索拉力先升后降，中后期出现峰值。

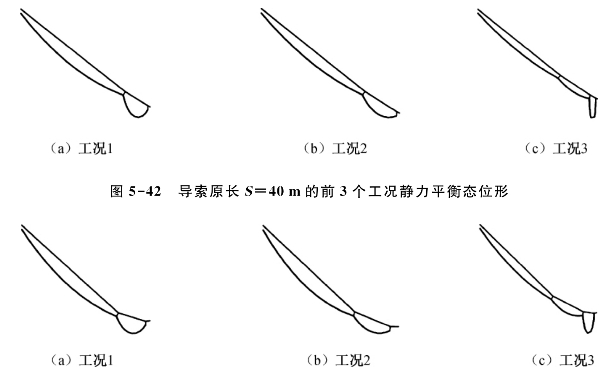
图5-43　导索原长S＝40.84m的前3个工况静力平衡态位形

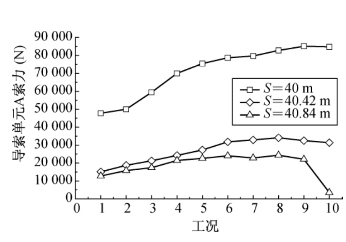
图5-44　导索不同长度条件导索拉力变化曲线

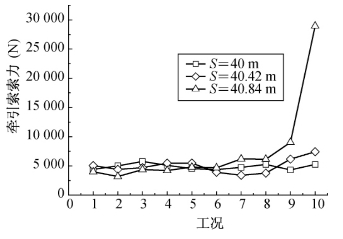
图5-45　导索不同长度条件牵引索拉力变化曲线

（2）导索原长较短（S＝40m）时，导索拉力明显增加，且末期拉力降低幅度小。

（3）随牵引过程，牵引索拉力总体变化不大，但当导索原长较长（S＝40.84m）时，末期牵引索拉力迅速增加。

（4）三个导索原长中，中间值S＝40.42m避免了过大的导索拉力或牵引索拉力，显然是较优的选择。

总之，导索和牵引索的拉力变化受导索原长影响大，且较为敏感；合理的导索原长应介于主索原长和两端距离之间。

表5-4　三种导索原长下导索拉力　单位：kN

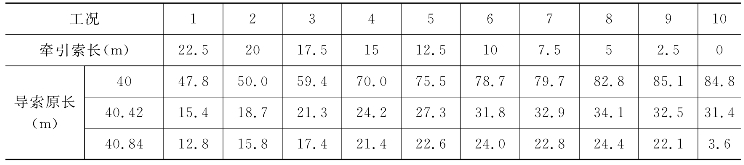
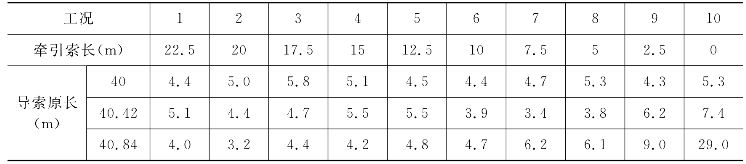
表5-5　三种导索原长下牵引索拉力　单位：kN