一、分析思路

NDFEM找形分析的主要内容是非线性动力平衡迭代和位形更新迭代，其总体步骤为：建立初始有限元模型；进行非线性动力有限元分析，当总动能达到峰值时更新有限元模型，重新进行动力分析，直到位形迭代收敛；最后对位形迭代收敛的有限元模型进行非线性静力分析，检验静力平衡状态；提取分析结果［43－44］。NDFEM法找形分析流程见图5-33所示。

二、具体步骤

NDFEM法的具体步骤如下：

1）分析准备

明确索杆系的设计成型状态和施工方案，以及所需要分析的施工阶段。

2）建立初始有限元模型

选用满足工程精度要求的索单元和杆单元；按照设计成型态位形或其他假定的初始位形建立有限元模型；根据所需分析的施工阶段，施加重力和其他荷载（如吊挂荷载）以及边界约束条件；按照式（5-8）和式（5-9），根据索杆原长已知的条件，在索杆上施加等效初应变（εp）或等效温差（ΔTp），按照式（5-10）和式（5-11），根据索杆内力（如牵引力、张拉力等）已知的条件，在索杆上施加εp或ΔTp。

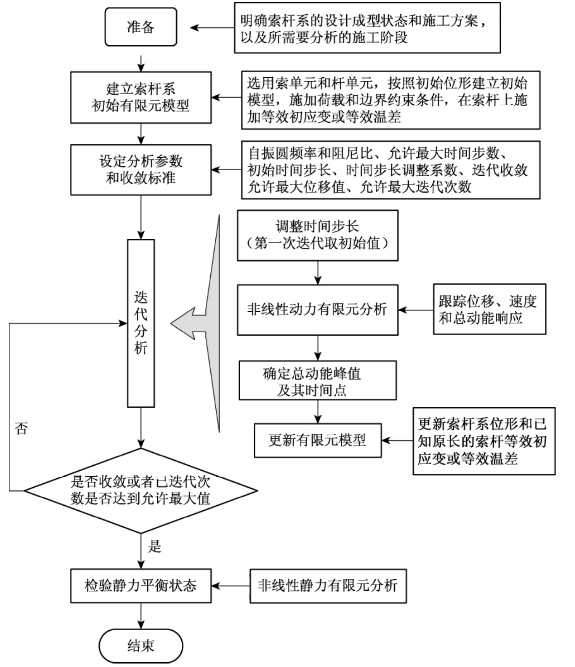
图5-33 NDFEM法找形分析流程

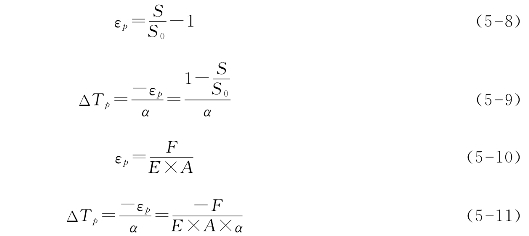
式中，S为模型中单元长度；S0为单元原长；E、A、α分别为弹性模量、截面积和温度膨胀系数；F为索杆内力。

3）设定分析参数

设置单次动力分析时间步数允许最大值［Nts］、单个时间步动力平衡迭代次数允许最大值［Nei］、初始时间步长ΔTs（1）、时间步长调整系数Cts、动力平衡迭代位移收敛值［Uei］、位形更新迭代位移收敛值［Uci］、位形迭代允许最大次数［Nci］。

动力平衡方程（式（5-12））可采用Rayleigh阻尼矩阵（式（5-13）），其中自振圆频率和阻尼比可虚拟设定。

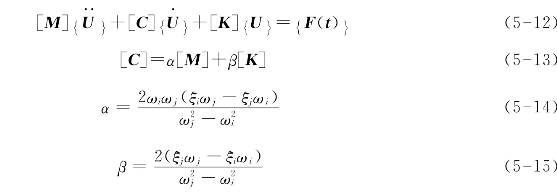
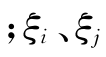式中分别为位移向量、速度向量和加速度向量；｛F（t）｝为荷载时程向量；［C］为Rayleigh阻尼矩阵；［M］为质量矩阵；［K］为刚度矩阵；α、β为Rayleigh阻尼系数；ωi、ωj分别为第i阶和第j阶自振圆频率分别为与ωi和ωj对应的阻尼比。

若则式（5-14）和式（5-15）可简化为式（5-16）和式（5-17）：

4）迭代分析

（1）调整第m次动力分析的时间步长ΔTs（m）。

（2）非线性动力有限元分析：建立非线性动力有限元平衡方程（式（5-12）），按照时间步长ΔTs（m）连续求解，跟踪索杆系的位移、速度和总动能响应；当索杆系整体运动方向明确时，为加快向静力平衡位形运动，提高分析效率，可不考虑阻尼力，建立无阻尼运动方程（式（5-18））。

（3）确定总动能峰值及其时间点。

（4）更新有限元模型，包括更新索杆系的位形以及控制索杆的原长或者内力：

当判断出总动能峰值及其时间点后，更新有限元模型，采用线性插值的方法计算与总动能峰值E（p）对应的时间点Ts（p）的位移，更新索杆系位形。

模型更新包括位形更新、内力更新和原长更新。按照动力分析位移更新节点坐标后，模型中构件长度也改变了。索结构中常以等效初应变或等效温差来模拟拉索张拉或者控制原长。对于需控制原长的构件，则以更新前后原长不变为原则，根据更新后的长度调整等效初应变或者等效温差，即更新内力；对于需控制内力（如提升牵引力和张拉力等）的构件，则不调整等效初应变或者等效温差，即更新原长。

5）判断是否收敛或者位形已更新次数Nci是否达到［Nci］(www.daowen.com)

（1）若更新有限元模型节点最大位移Uci（m）小于［Uci］时，位形迭代收敛，进入第6）步。

（2）若Uci（m）＞［Uci］，且Nci＜［Nci］，则进入下一次的位形迭代，重新回到第4）步。

（3）若Uci（m）＞［Uci］，但Nci＝［Nci］，则结束分析。

6）检验静力平衡态

若时间步长ΔTs或允许最大时间步数［Nts］取值过小，则可能动力分析位移过小，满足位形更新迭代收敛标准，却并不满足静力平衡。为避免“假”平衡，需对满足收敛条件的更新位形进行静力平衡态的检验。采用非线性静力有限元进行分析，良好结果应该是分析极易收敛，且小位移满足精度要求。整个流程示意图见图5-33所示。

三、分析参数及收敛准则

1）时间步长及其调整

时间步长ΔTs是决定NDFEM法找形分析收敛速度的关键因素之一。ΔTs越短，则动力分析越易收敛，但达到静力平衡的总时间步数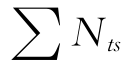更多，分析效率低。在某次动力分析中，合理的ΔTs应保证动力分析收敛前提下，在较少的时间步数Nts内总动能达到峰值。NDFEM法找形分析可分为初期、中期和后期三个阶段：

（1）在初期阶段，索杆系运动剧烈，动力分析可设置较小的时间步长，便于动力平衡迭代收敛。

（2）在中期阶段，索杆系主位移方向明确，趋向静力平衡位形，此时应设置较大的时间步长，从而在较少的时间步数和位形更新次数下迅速接近静力平衡态。

（3）在后期阶段，索杆系在静力平衡态附近振动，此时应设置更大的时间步长，从而使位形迭代尽快收敛，达到静力平衡状态。

鉴于时间步长对动力平衡迭代和分析效率有重要的影响，提出在分析过程中采用时间步长调整系数Cts对各次动力分析的时间步长自动调整，调整策略为：①第一次位形迭代采用初始时间步长ΔTs（1）；②若第m－1次动力分析的时间步数Nts（m－1）＝［Nts］，总动能仍未出现下降，则第m次动力分析的时间步长ΔTs（m）＝ΔTs（m－1）×Cts；③若第m－1次动力分析不收敛，则ΔTs（m）＝ΔTs（m－1）／Cts。

2）总动能峰值E（p）及对应时间点T（p）的确定

动力分析中第k时间步的结构总动能E（k）为：

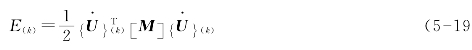
式中为第k时间步的速度向量。

图5-34　总动能峰值及其时间点

确定总动能峰值及其时间点的策略为：

（1）设E（0）＝0。

（2）当第k时间步动力平衡迭代收敛时，若k＜［Nts］，E（k）＞E（k－1），则总动能未达到峰值，继续本次动力分析，进入第（k＋1）时间步；若k≤［Nts］，E（k）＜E（k－1），则将三个连续时间步的总动能E（k）、E（k－1）、E（k－2）进行二次抛物线曲线拟合，计算总动能曲线的峰值E（p）及其时间点Ts（p）（图5-34）；若k＝［Nts］，E（k）≥E（k－1），则E（p）＝E（k），Ts（p）＝Ts（k）。

（3）当第k时间步动力平衡迭代不收敛时，若k＝1，则不更新位形，在调整时间步长后进入下次动力分析；若1＜k≤［Nts］，则E（p）＝E（k－1），Ts（p）＝Ts（k－1）。

3）迭代收敛准则

NDFEM法找形分析中存在两级迭代：一级是动力平衡迭代，二级是位形更新迭代。

一般非线性动力有限元分析中，动力平衡迭代的收敛标准包括力和位移两项指标，但鉴于NDFEM法找形分析中需多次更新位形，并根据更新的位形按照原长或内力一定的原则，重新确定索杆中的等效初应变或等效温差，因此为便于收敛且不影响最终分析结果，动力平衡迭代仅需设置位移收敛标准［Uei］。

位形更新迭代也仅设置位移收敛标准［Uci］。若更新有限元模型的节点最大位移Uci≤［Uci］，则位形更新迭代收敛。