进行风振瞬态分析后，获得各样本的响应时程。对某个样本i的某种响应（如位移和内力等）时程进行数值统计，求出响应均值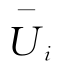、均方差σi，按下式计算该样本的响应最大值Ui和风振系数βi。对所有样本的风振系数进行统计，确定该响应的结构整体风振系数β，用于结构风载静力分析。

式中，μ为峰值因子或保证系数。由于μ涉及安全度，各国可有不同标准。根据我国可靠指标规定的数值，我国规范μ取值在2.2（保证率98.61%）左右，因此μ取值2.2。

（1）选择典型节点和单元作为样本，各风振响应时程见图4－43～图4－46所示。可见，索网节点位移、面索应力和支座径向位移的变化幅值都较小，而下拉索的应力变化极值约为65MPa，拉力变化极值约为9kN。

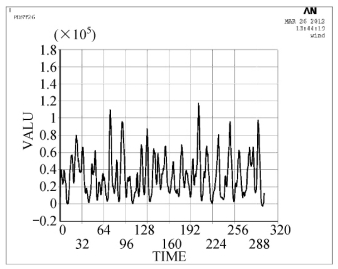
图4－43　典型索网节点竖向位移时程（m）

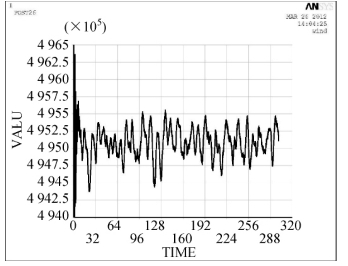
图4－44　典型面索应力时程（N／m2）

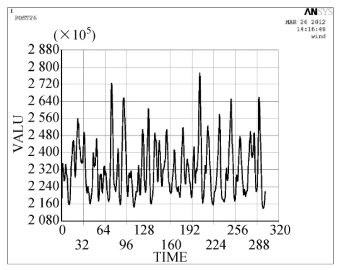
图4－45　典型下拉索应力时程（N）

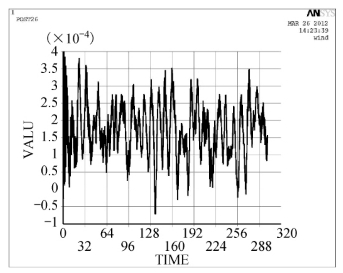
图4－46　典型滑动支座柱面径向位移时程（m）

（2）下拉索应力响应统计。由于结构风振分析的初始状态为初始荷载作用下的平衡态，因此在风振前结构存在初始位移和初始内力，这对早期风振的结构状态有一定影响，并影响到风振响应统计值。为避免这个影响，风振参数从10s开始统计，且风振各响应值均减去了初始状态下的相应值，得到纯风振下的响应值。

考虑到风振主要对下拉索影响较大，因此对各五分之一主轴上的下拉索风振应力进行统计，结果见表4－21、图4－47～图4－50所示。可见：

①下拉索风振应力的平均值为10～63MPa（拉力1.4～8.8kN），最大值为20～115MPa（拉力2.8～16.1kN），风振系数为1.6～2.5。

②从内向外，下拉索风振应力平均值总体增大，但最外环由于受风面积小，所以较低。

③从内向外，下拉索风振系数总体减小，建议总体风振系数取2.0。(www.daowen.com)

④轴线4和5位于风向的上游，轴线2和3位于风向的下游，轴线1正好位于中间，因此轴线4和5的下拉索风振应力统计参数较大。

⑤未见明显的共振现象。

表4－21　五分之一主轴的下拉索风振应力统计

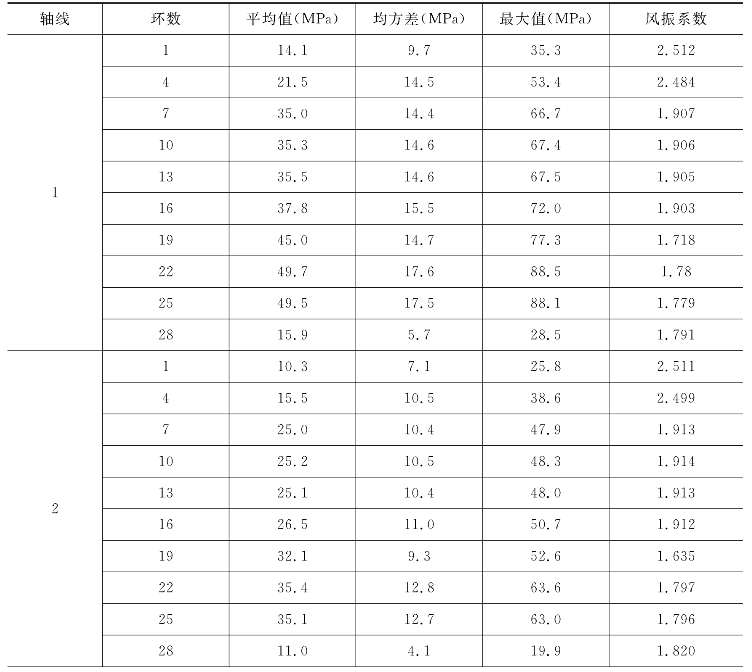
续表

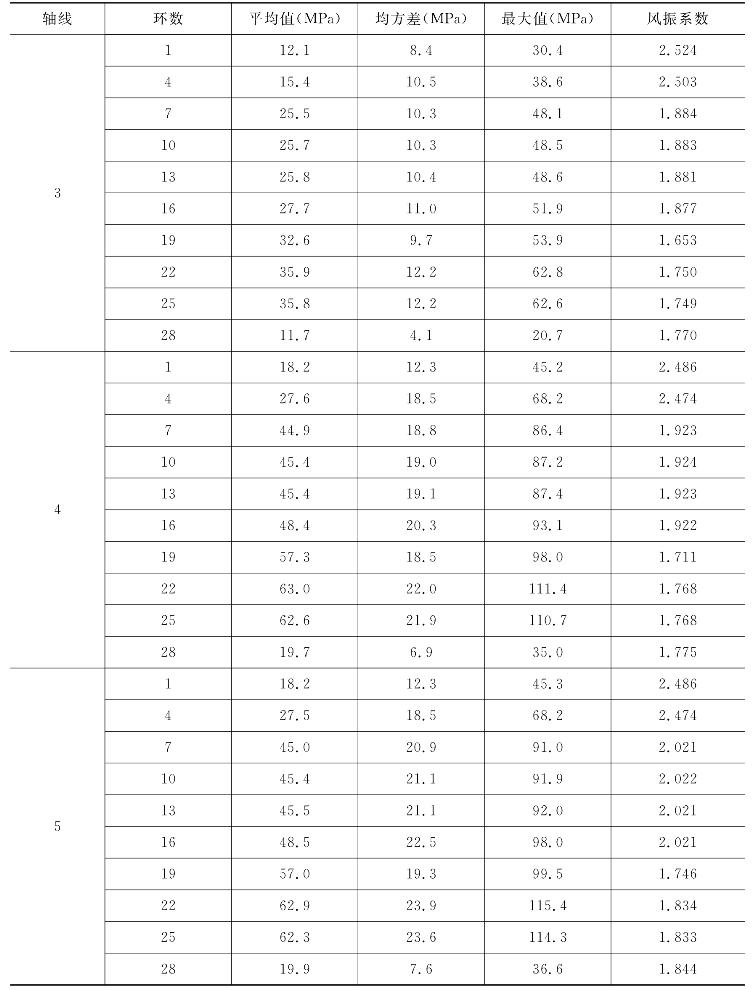
注：第1环为最内环，其他环从内向外递推。

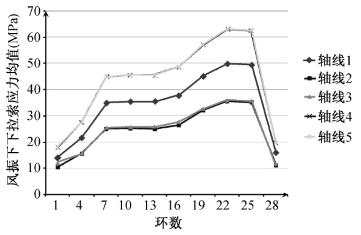
图4－47　主轴下拉索风振应力的平均值

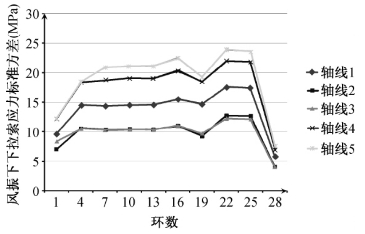
图4－48　主轴下拉索风振应力的均方差

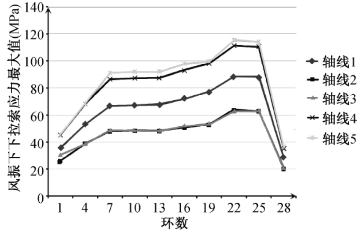
图4－49　主轴下拉索风振应力的最大值

图4－50　主轴下拉索风振应力的风振系数